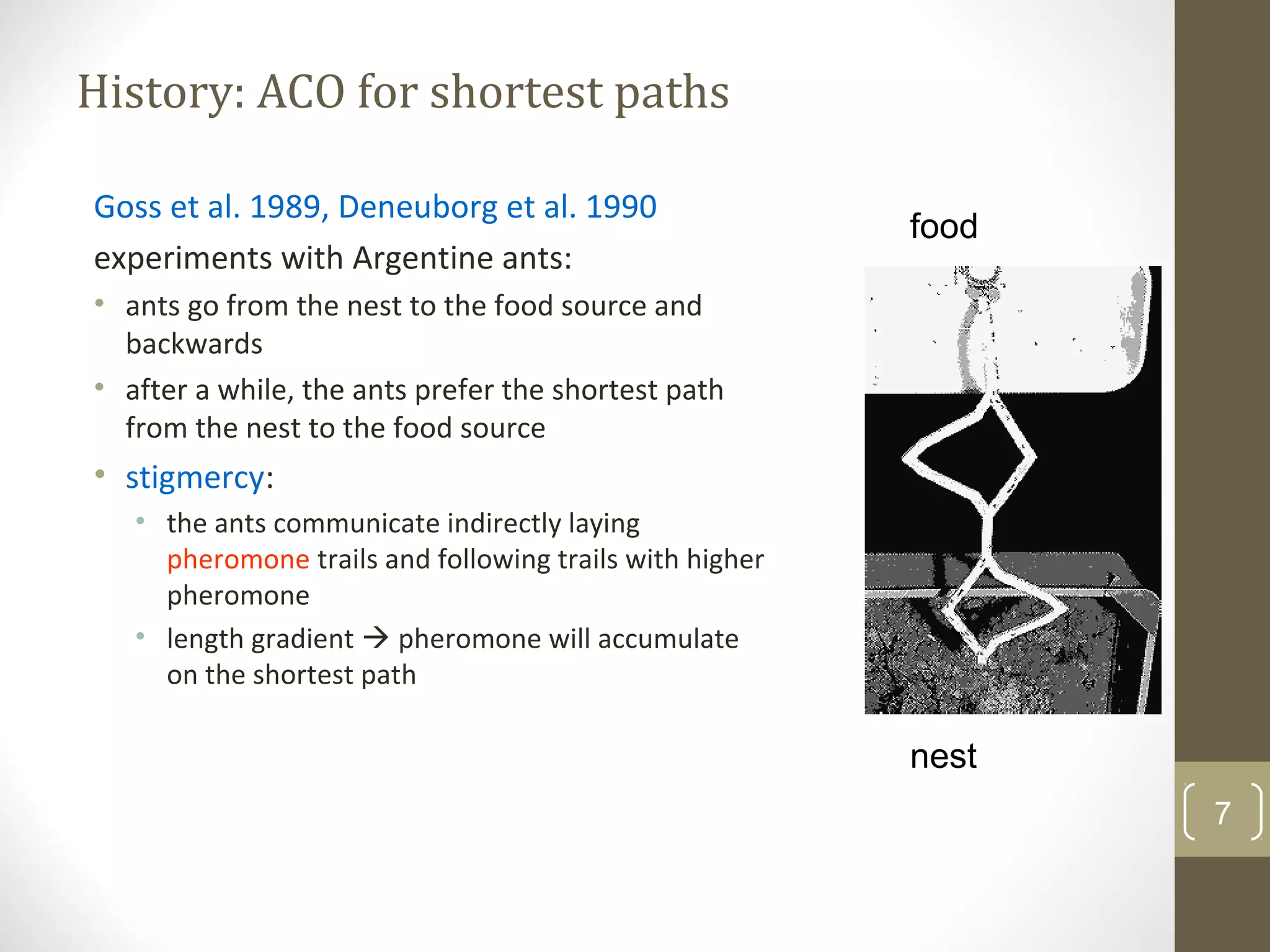
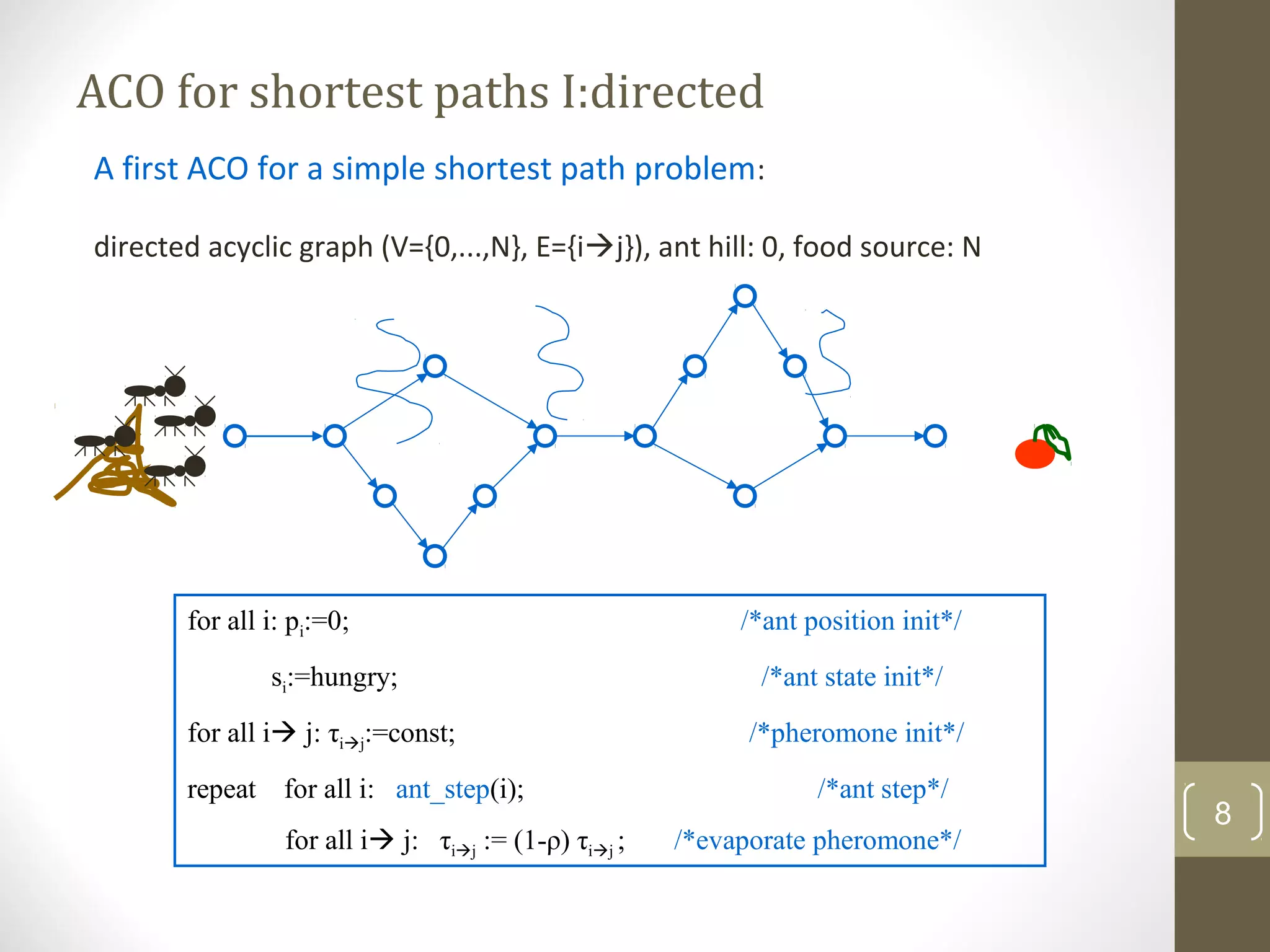
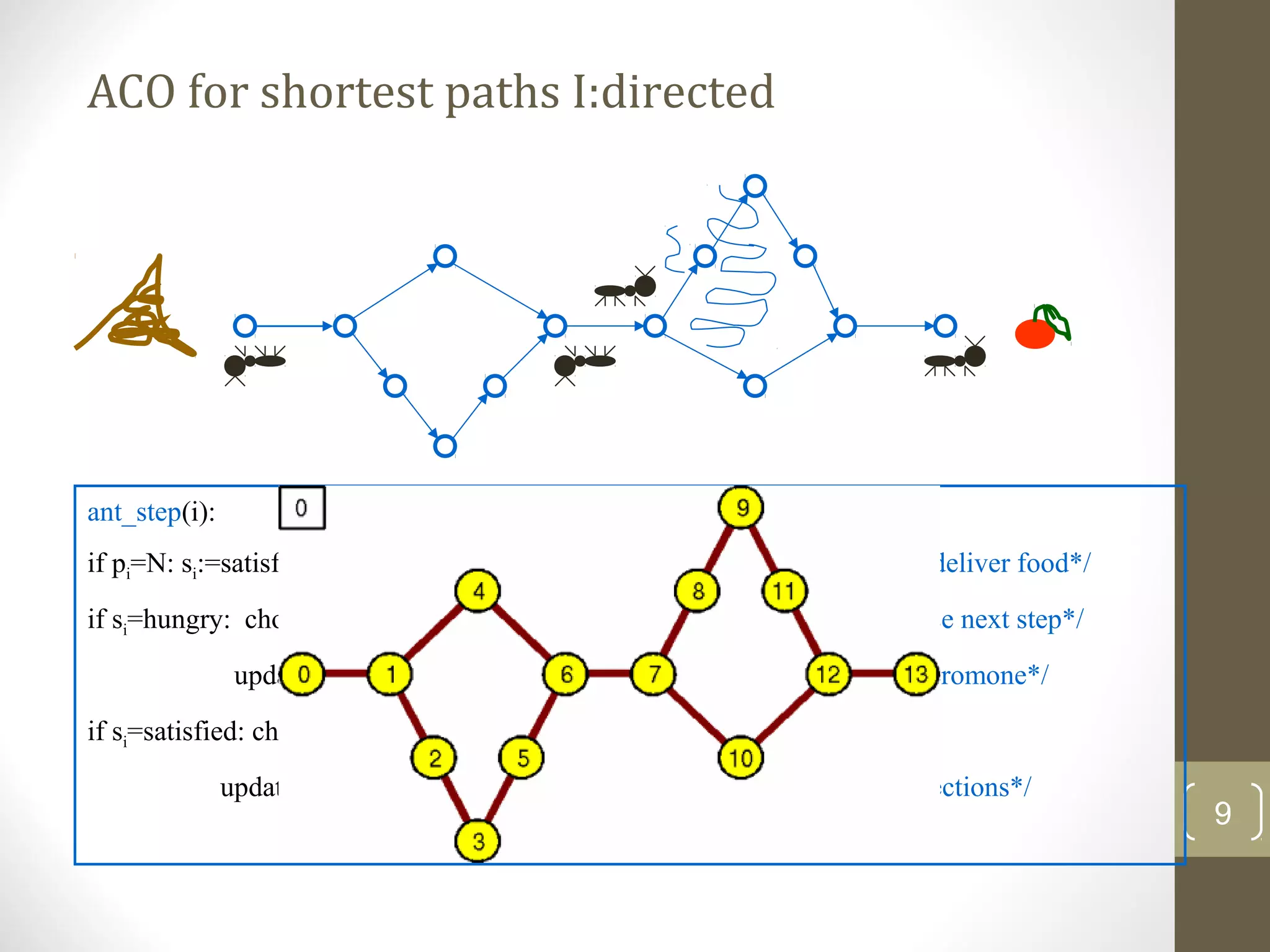
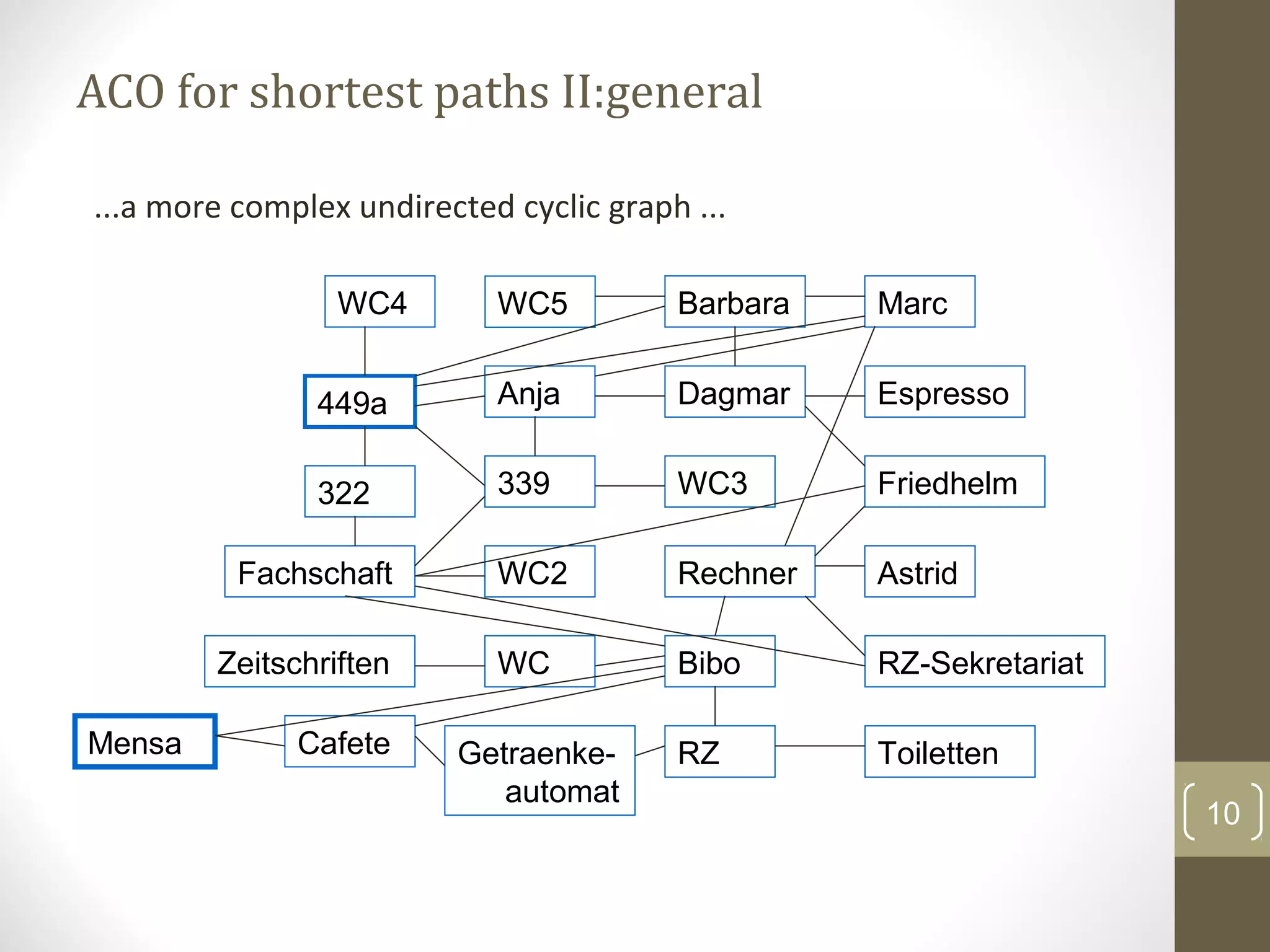
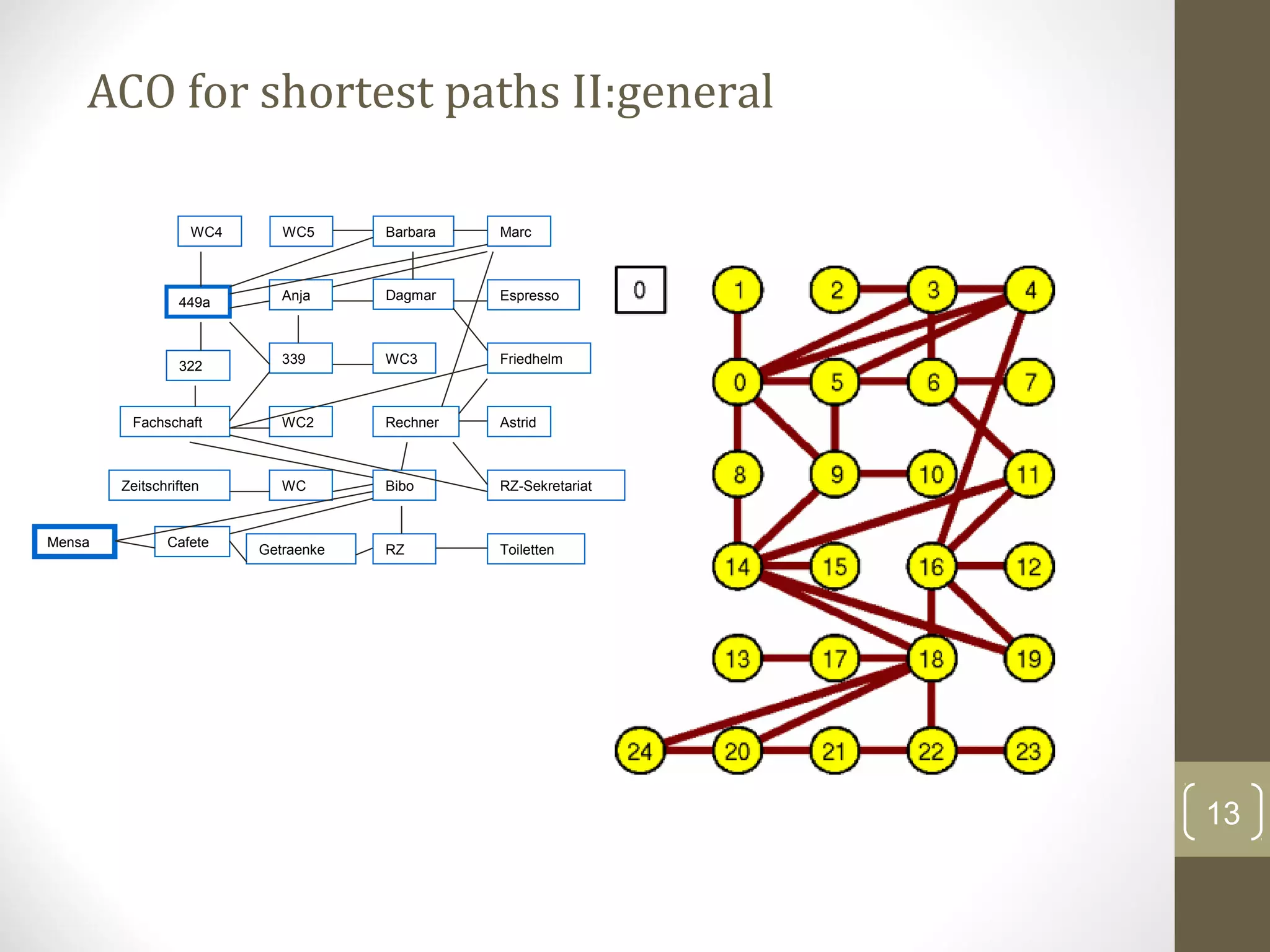
Ant Colony Optimization (ACO) is a heuristic optimization technique inspired by the behavior of real ant colonies. It is used to find solutions to optimization and shortest path problems. The technique works by simulating ants walking between points, such as between their nest and food sources. As artificial ants walk, they lay down and follow pheromone trails. Over time, the shortest paths become more desirable as they have the most pheromone accumulated on them. The algorithm iteratively improves the solutions found via the probabilistic decisions of many agents (the artificial ants) based on local information and global pheromone trails.

1. Ant Colony Optimization
By:
Sachin Agarwalla
Regd. No-0911012065
C.S.E(A)
Under Guidance Of:
Mr. Swadhin Ku. Barisal
B.E., M.Tech., CSE (IIT, Kharagpur)
Assistant Professor 1
I.T.E.R

2. Optimization
General optimization problem:
given f:Xℝ,
find xεX such that f(x) is minimum
• Given a graph with two specified vertices A and B, find a shortest path
from A to B.
 shortest path problem, polynomial
2

3. Ant colony food
3
nest

4. Ant Colony Optimization (ACO):
a heuristic optimization method for shortest path
and other optimization problems which borrows
ideas from biological ants
4

5. Ant Colony Optimization
Outline
• History: ACO for shortest paths
• ACO for shortest paths I: directed
• ACO for shortest paths II: general
• Advantages and Disadvantages
• Summary
• References
5

6. History: ACO for shortest
paths …
6

7. History: ACO for shortest paths
Goss et al. 1989, Deneuborg et al. 1990
food
experiments with Argentine ants:
• ants go from the nest to the food source and
backwards
• after a while, the ants prefer the shortest path
from the nest to the food source
• stigmercy:
• the ants communicate indirectly laying
pheromone trails and following trails with higher
pheromone
• length gradient  pheromone will accumulate
on the shortest path
nest
7

8. ACO for shortest paths I:directed
A first ACO for a simple shortest path problem:
directed acyclic graph (V={0,...,N}, E={ij}), ant hill: 0, food source: N
for all i: pi:=0; /*ant position init*/
si:=hungry; /*ant state init*/
for all i j: τij:=const; /*pheromone init*/
repeat for all i: ant_step(i); /*ant step*/
8
for all i j: τij := (1-ρ) τij ; /*evaporate pheromone*/

9. ACO for shortest paths I:directed
ant_step(i):
if pi=N: si:=satisfied; if pi=0: si:=hungry; /*collect food/deliver food*/
if si=hungry: choose j with pij with probability τpi j/Σpij’τpij’ /*choose next step*/
update Δτpi j := ε; pi:=j; /*update pheromone*/
if si=satisfied: choose j with jpi with probability τjpi/Σj’piτj’pi
update Δτjpi:= ε; pj:=i; /* reversed directions*/
9

10. ACO for shortest paths II:general
...a more complex undirected cyclic graph ...
WC4 WC5 Barbara Marc
449a Anja Dagmar Espresso
322 339 WC3 Friedhelm
Fachschaft WC2 Rechner Astrid
Zeitschriften WC Bibo RZ-Sekretariat
Mensa Cafete Getraenke- RZ Toiletten
automat
10

11. ACO for shortest paths II:general
... Marc was not so happy with the result ...
449a
449a
11

12. ACO for shortest paths II:general
for all i: pi:=0; /*ant position init*/
si:=hungry
si:=( ); /*ant brain is empty*/ minibrain
for all i-j: τi-j:=const; /*pheromone init*/
repeat for all i: construct_solution(i);
repeat for all i: ant_step(i);
for all i: global_pheromone_update(i);
for all i-j: τi-j := (1-ρ) τi-j; /*evaporate*/
construct_solution(i):
while pi≠N /*no solution*/
choose j with pi-j with probability τpi-j / Σpi-j’τpi-j’;
pi:=j;
minibrain
append j to si; /*remember the trail*/
global_pheromone_update(i):
update according
for all j-j’ in si: Δτj-j’:= 1/length of the path stored in si; 12
to the quality

13. ACO for shortest paths II:general
WC4 WC5 Barbara Marc
Anja Dagmar Espresso
449a
339 WC3 Friedhelm
322
Fachschaft WC2 Rechner Astrid
Zeitschriften WC Bibo RZ-Sekretariat
Mensa Cafete
Getraenke RZ Toiletten
13

14. ACO for shortest paths
init pheromone ti-j ;
repeat for all ants i: construct_solution(i);
for all ants i: global_pheromone_update(i);
for all edges: evaporate pheromone;
construct_solution(i):
init ant;
while not yet a solution:
expand the solution by one edge probabilistically
according to the pheromone;
global_pheromone_update(i):
for all edges in the solution:
increase the pheromone according to the quality;
14

15. Advantages and Disadvantages
Advantages :
1) Positive feedback accounts for rapid discovery of good solution.
2) Efficient for Travels salesman problem and other similar problem.
3) Can be use in dynamic application.
Disadvantages :
1) Theoretical analysis is difficult.
2) Probability distribution changes by iteration.
3) Time to convergence is uncertian.
15

16. Summary
• Artificial Intelligence technique used to develop a new method to solve problems
unsolvable since last many years
• ACO is a recently proposed metaheuristic approach for solving hard combinatorial
optimization problems.
• Artificial ants implement a randomized construction heuristic which makes probabilistic
decisions
• ACO shows great performance with the “ill-structured” problems like network routing
16

17. References
• M. Dorigo, M. Birattari, T. Stützle, “Ant Colony Optimization – Artificial Ants as a
Computational Intelligence Technique”, IEEE Computational Intelligence Magazine,
2006
• C. Blum, Theoretical and Practical Aspects of Ant Colony Optimization, Dissertations
in Artificial Intelligence, Vol. 282, Akademische Verlagsgesellschaft Aka GmbH, Berlin,
Germany, 2004.
• Wikipedia.com
17

18. Questions ?
18

19. Thank You !
19