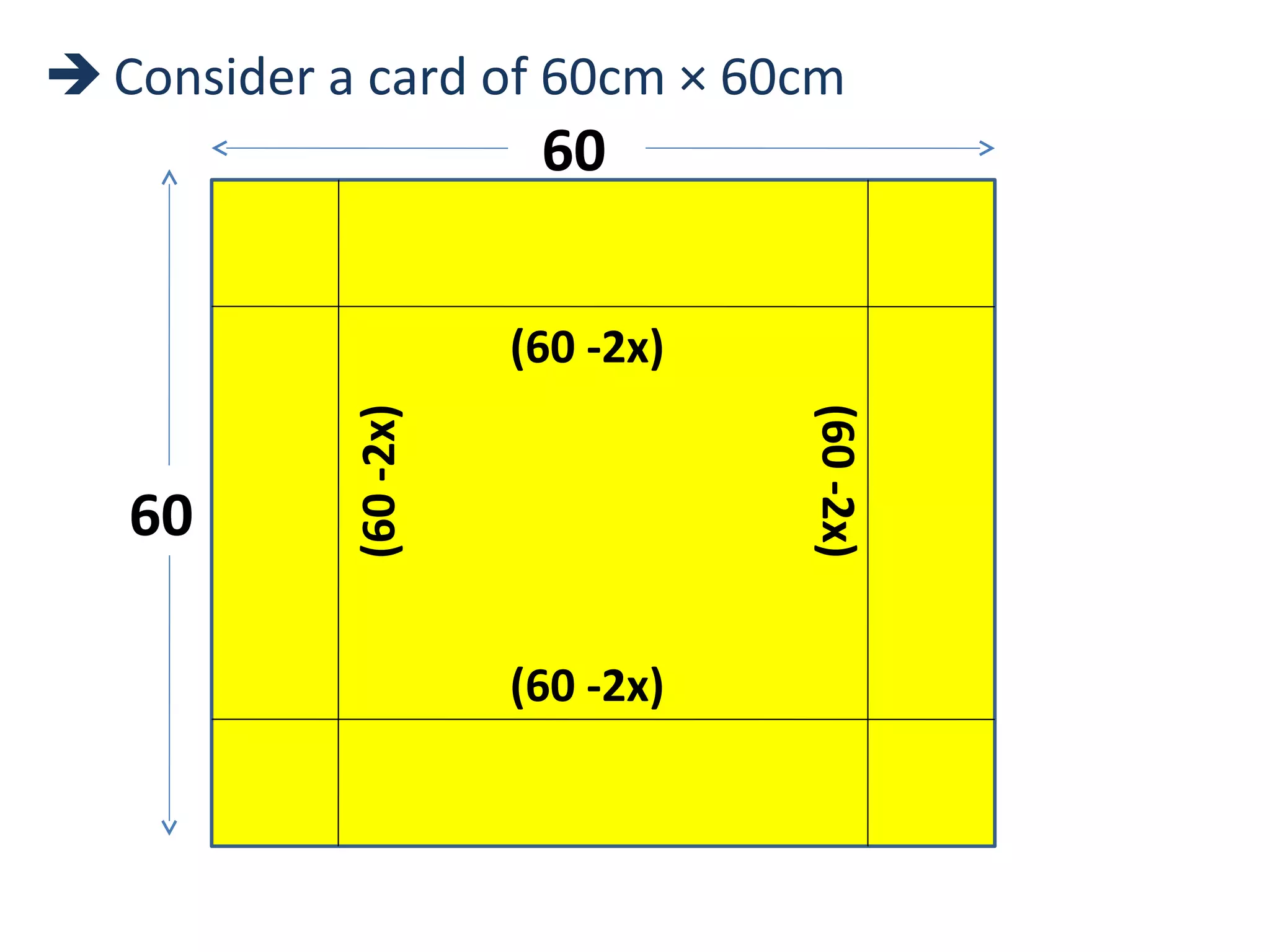
The document discusses the history and applications of calculus, tracing its origins to inventors like Newton and Leibniz, as well as contributions from ancient mathematicians such as Brahmagupta and Bhaskracharya. It explains calculus as a study of change through differentiation and integration, providing practical applications such as maximizing box volume and predicting outcomes in various fields. Additionally, it illustrates the use of calculus in real-world scenarios, including Newton's law of cooling and its implications in crime investigation.

1. Application of…
…to the real

2. Introduction
&
History
of
Calculus
-Divyarajsinh

3. C a l c u l u s
What does it mean ?
Who invented it?
What we study in Calculus?
What was the need to invent it?

4. C a l c u l u s
Latin Word Small stones used for
counting

5. Who is the first to invent Calculus?
Newton Leibnitz

6. Who is the first to invent Calculus?
Brahmagupta
“Yuktibhasha” is considered to be
the first book on Calculus…!!

7. Bhaskracharya
He used principle of
differential calculus in
problems on Astronomy.
He is pioneer of some
principles of differential
calculus.
He stated Rolle’s Mean Value Theorem in his book
“Siddhant Shiromani”…!!!!

8. What we study in Calculus?
Geometry Algebra
Calculus is study of ‘Change’

9. What was the need to invent it?
We can find the area of above shapes
with the help of Geometrical tools.

10. But What about these shapes…!!???

11. ContinuousDiscrete

12. ContinuousDiscrete
1
+
1
+
1
10
Drops ?

13. “We need a continuous
summation tool.”
This idea leads to the
invention of Calculus.

14. Calculus
● Integration● Differentiation

15. Integration
 Origin from the word ‘to integrate’ or ‘to merge’.
 In 18th century the calculation of area and volume
are done using integration.

16. Differentiation
 Differentiate means ‘to separate’.
In calculus derivative is a measure of how a
function changes as its input changes.
dv
dt
= a
v = velocity,
a = acceleration

17. Uses of
Calculus
&
Mathematical Modeling
-Milan Patel

18. 1) Save money on experiments.
2) Perform impossible experiments.
3) Predict the future…!!

19. Assume that you are a General
Manager of a company which
produces open top boxes for fruit
market…

20. To make open top boxes for
fruit market, using square
sheet of card board.
To maximize the volume of
box in order to increase the
profit of the company.

21. Steps to solve this problem…
Create Mathematical Model
Solve it mathematically
Justify the answer

22. How to create a mathematical model?
Understand

23.  Consider a card of 60cm × 60cm
60
60
(60 -2x)
(60 -2x)
(60-2x)
(60-2x)

24. Volume of the box,
V = L × B × H
= (60-2x) × (60-2x) × (x)
= 4x – 240x + 3600x
3 2

25. Now, We will use…

26. = 4x – 240x + 3600x
3 2
V
dV = 12x - 480x + 3600 = 0
2
dx
x - 40x + 300 = 0
2
(x-30) (x-10) = 0
x = 30cm & x = 10cm

27. Substitute x=10cm to find volume :-
= 4x – 240x + 3600x
3 2
V
= 4(10)– 240(10) + 3600(10)
3 2
= 16000 cm3

28. Justify the Answer :-
Application of second derivative
dV = 12x - 480x + 3600
dx
d V = 24x - 480
dx
2
2
2
d V = 24(10) – 480 = -240 < 0
dx
2
2
x=10

29. Cut the square of 10 cm X 10 cm
from the corner in order to
maximize the volume of the box.

30. Useful
Applications
of
Calculus
-Saumil Patel

31. Average Value
Area b/w Curves
Length of Arc

32. Average value
5 6 3 2 4+ + + +
5
= 4

33. Average value
1
2
3
4
5
6
7
1 2 3 5 64 7
f(x)
5 5 5 5 5
a b

34. Average value
Average value of f(x) in given interval
5 5 5 5 5+ + + +
5
= 5
=

35. -1
0
1
Average value
f(x)
a b

36. Average value
favg = 1
b-a
f(x) dx
a
b

37. Application to the real world
Average growth of tree in given time period

38. Application to the real world
Average growth of bacteria

39. Application to the real world
Average amount of water falling
from the water fall

40. Area under the curve
We know that the integral…
f(x) dx
a
b
denotes the area bounded by the curve y=f(x)
from x=a to x=b.
x=a x=b
y=f(x)

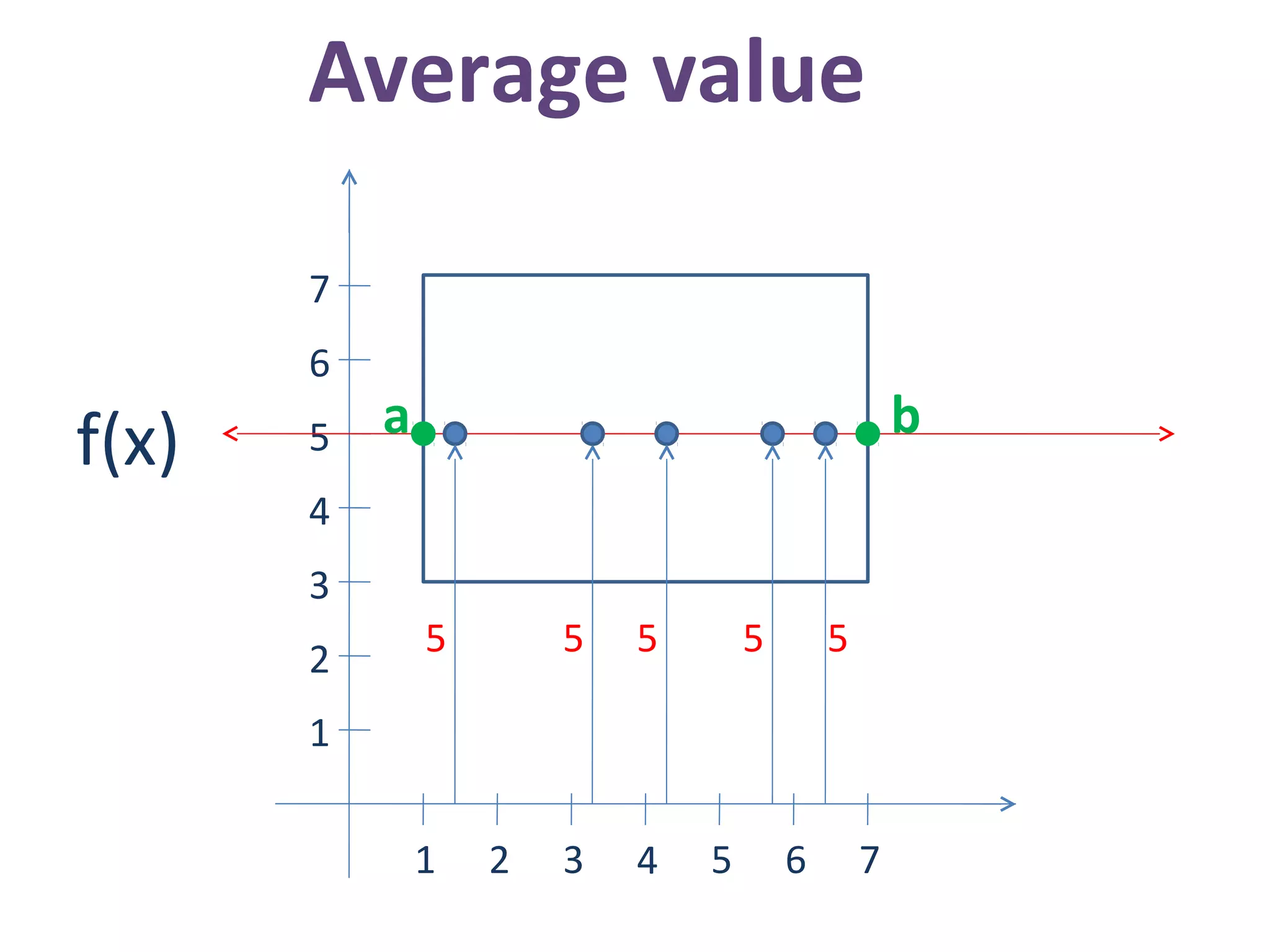
41. Area between curves
x=a x=b
f(x)
g(x)
Area b/w curves = [Area under f(x)]
-[(Area under g(x)]

42. Area between curves
= -f(x) dx
a
b
g(x) dx
a
b
= [f(x) - g(x)]dx
a
b

43. Application to the real world

44. Length of arc
a b
Length of arc = b-a
f(x)

45. Length of arc
a
b
Length of ab = b-a

46. Length of arc
a
b
c
(Length of ac) + (Length of cb)

47. Length of arc
a
b
d
c
e
(Length of ad) + (Length of dc) +
(Length of ce) + (Length of eb)

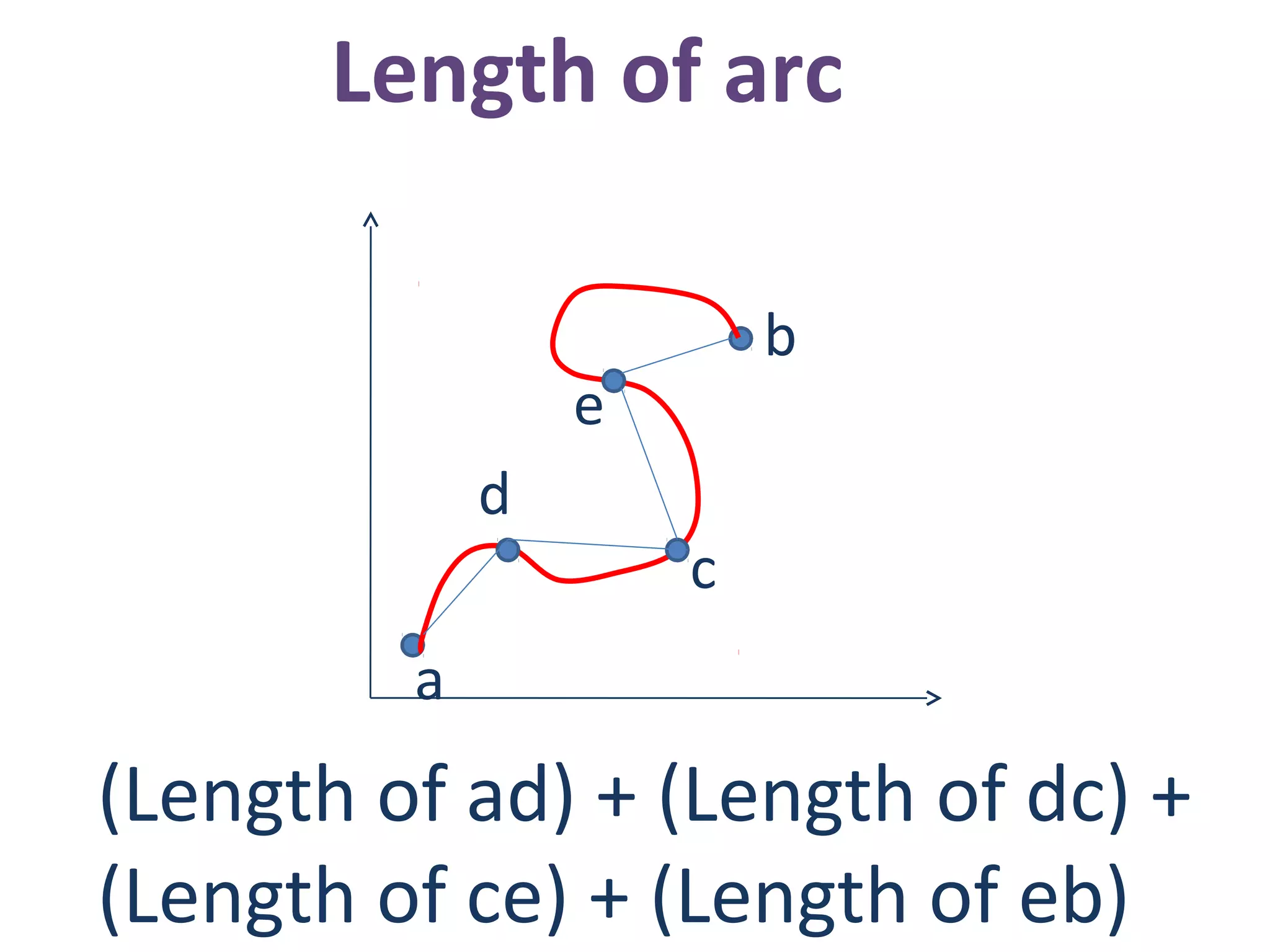
48. Length of arc
a
b
Length of arc =
1+[f’(x)] dx
2

49. Application to the real world

50. Application to the real world

51. Newton’s Law of
cooling
&
It’s Applications
-Richa Raval

52. “Rate of change of the temperature of an
object is proportional to the difference
between its own temperature and the
temperature of its surroundings.”
“Newton’s law of cooling”

53. Applying Calculus…
dT (T-Te)α
dt
dT
dt
= -k(T-Te) (‘k’ is a +ve constant)
dT
(T-Te)
= -k.dt
Integrating on both sides we get…
ln(T-Te)+C = -kt
At time t=0, temperature T=To…
C = -ln(To-Te)
…………………(1)

54. Substitute the value of ‘C’ in (1)…
ln = -kt
T-Te
To-
Te
= e
T-Te
To-
Te
-kt
T-Te = (To-Te) e
-kt
T = Te + (To-Te) e
-kt
…………………(2)

55. Application of
“NEWTON’S
LAW OF
COOLING”In
Crime Investigation

56. Detective came at 10:23 a.m.
Temperature of body :- 26.7 C
Temperature of room :- 20 C
After an hour…
Temperature of body :- 25.8 C
Assume that body temperature was normal i.e. 37 C
What is time of death ?

57. T = Te + (To-Te) e
-kt
Let the time of death be ‘x’ hour before the arrival of
detective.
Substitute given values in equation (2)…
T(x) = 26.7 = 20 + (37-20) e-kx
T(x+1) = 25.8 = 20 + (37-20) e-k(x+1)
Solving above two equations…
0.394 = e-kx
0.341 = e-k(x+1)
Taking log on both sides of above two equations…
ln(0.394) = -kx
ln(0.341) = -k(x+1)
…………………(3)
…………………(4)

58. Divide equation (3) by (4)…
ln(0.394) -kx
ln(0.341) -k(x+1)
=
=0.8657
x
(x+1)
x = 7 hour
Murder took place 7 hour before arrival of detective.
i.e. 3:23 p.m.

59. Computer Manufacturing
T = Te + (To-Te) e
-kt
27 = 20 + (50-20) e-0.5k
K=2.9

60. SomeImportant
Applicationsof
Calculus…

61. Growth of bacteria

63. Construction Technology

65. Thank you…