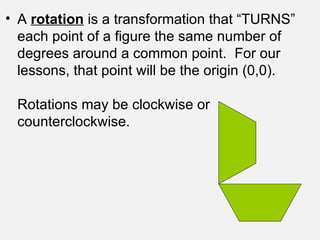
The document is about transformations, specifically translations and rotations. It provides examples of performing different types of rotations on sets of points, including 90° clockwise rotations, 90° counterclockwise rotations, and 180° rotations. It explains that a 90° clockwise rotation switches the x and y coordinates and changes the sign of y, a 90° counterclockwise rotation switches the x and y coordinates and changes the sign of x, and a 180° rotation changes the sign of both the x and y coordinates. Several examples are worked through to demonstrate how to find the image of a set of points after a given rotation.

1. Daily Homework Quiz For use after Lesson 8.7 2. Where have you seen a translation today? 1. RST has vertices R (–1, 4) , S (3, 4) , and T (2, –3) . Find the vertices of its image after the translation ( x , y ) -> ( x – 4 , y + 5). ∆

2. Daily Homework Quiz For use after Lesson 8.7 2. Where have you seen a translation today? 1. RST has vertices R (–1, 4) , S (3, 4) , and T (2, –3) . Find the vertices of its image after the translation ( x , y ) -> ( x – 4 , y + 5). ∆ ANSWER R' (–5, 9), S' (–1, 9), T' (–2, 2)

3. Translations and Rotations Section 8.7 P. 439 - 443

4. Essential Questions What are the similarities and differences among transformations? How are the principles of transformational geometry used in art, architecture and fashion? What are the applications for transformations?

5. A rotation is a transformation that “TURNS” each point of a figure the same number of degrees around a common point. For our lessons, that point will be the origin (0,0). Rotations may be clockwise or counterclockwise.

6. A rotation is a transformation that “TURNS” each point of a figure the same number of degrees around a common point. For our lessons, that point will be the origin (0,0). Rotations may be clockwise or counterclockwise.

10. Rotation : 90 degrees clockwise switch the coordinates around, and Y will become the opposite sign of the original point. (y, -x) 90 degrees counterclockwise switch the coordinates around, and X will become the opposite sign. (-y, x) 180 degrees “ opposite” coordinates for both x and y. (-x, -y)

11. Try this on graph paper! A 90 degrees clockwise rotation will switch the coordinates around, and Y will become the opposite sign of the original point. Example P (6,2) P’ (2,- 6) Q (-3,4) Q’ ( , ) W(4,0) W’ ( , )

12. Graph A (1, 1), B (3, 1), C (3, 3), and D (1, 4) . Find its image after a 90° clockwise rotation. Switch the coordinates around, and Y will become the opposite sign of the original point. (y, -x) A’ (1,-1) B’ (1, -3) C’ (3, -3) D’ (4, -1)

13. GUIDED PRACTICE for Example 2 and 3 Graph A (1, 1), B (3, 1), C (3, 3), and D (1, 4) . Find its image after the given rotation. A’ (1,-1) B’ (1, -3) C’ (3, -3) D’ (4, -1) RULE: Switch the coordinates around, and Y will become the opposite sign of the original point. (y, -x) 2. 90 clockwise ANSWER

14. Try these on graph paper 90 degrees counterclockwise rotation will switch the coordinates around, and X will become the opposite sign. Example: P (5, 3) P’ (-3, 5) Q (-4,-2) Q’ (2, -4) W (-7, 8) W’ ( , )

15. Graph A (1, 1), B (3, 1), C (3, 3), and D (1, 4) . Find its image after a 90° counterclockwise rotation. Switch the coordinates around, and X will become the opposite sign. (-y, x) A’ (-1,1) B’ (-1, 3) C’ (-3, 3) D’ (-4, 1)

16. GUIDED PRACTICE for Example 2 and 3 Graph A (1, 1), B (3, 1), C (3, 3), and D (1, 4) . Find its image after the given rotation. A’ (-1,1) B’ (-1, 3) C’ (-3, 3) D’ (-4, 1) RULE: Switch the coordinates around, and X will become the opposite sign. (-y, x) 3. 90 counterclockwise ANSWER

17. 180 degree rotations will create “opposite” coordinates for both x and y. Example: P (4, 1) P’ (-4, -1) Q(-3, 5) Q’ (3, -5) W (2, -7) W’ ( , ) 180 degrees can be either clockwise or counterclockwise, the result is the SAME!

18. GUIDED PRACTICE for Example 2 and 3 Graph A (1, 1), B (3, 1), C (3, 3), and D (1, 4) . Find its image after a 180° rotation. “ opposite” coordinates for both x and y. (-x, -y) A’ (-1,-1) B’ (-3, -1) C’ (-3, -3) D’ (-1, -4)

19. GUIDED PRACTICE for Example 2 and 3 Graph A (1, 1), B (3, 1), C (3, 3), and D (1, 4) . Find its image after the given rotation. A’ (-1,-1) B’ (-3, -1) C’ (-3, -3) D’ (-1, -4) RULE: “opposite” coordinates for both x and y. (-x, -y) 4. 180 ANSWER

20. Homework Page 441 #1-3, 9, 11, 12