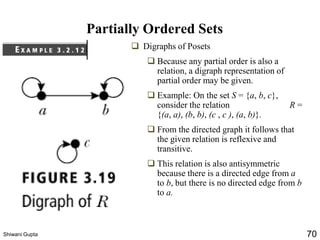
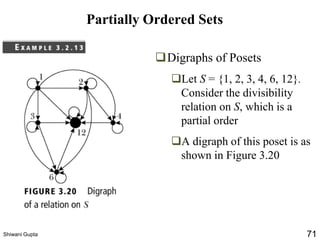
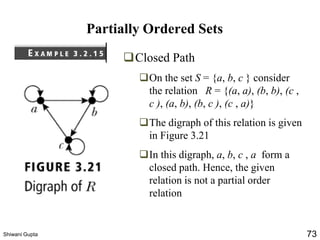
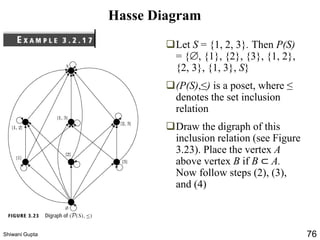
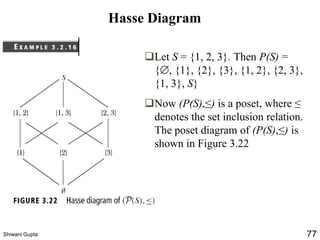
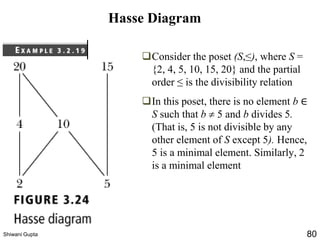
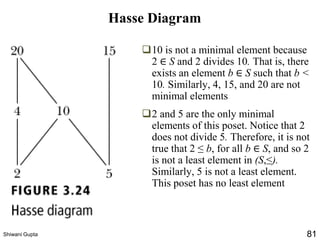
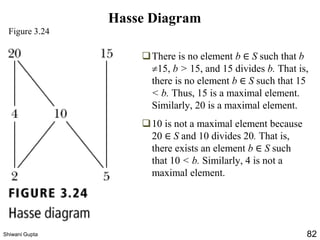
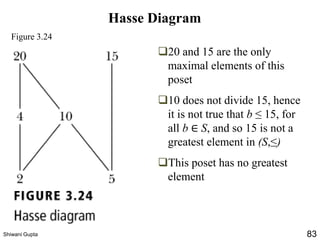
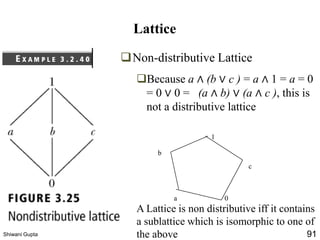
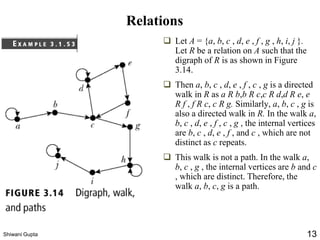
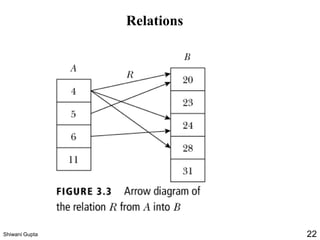
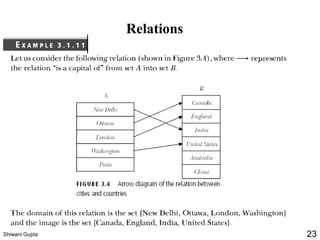
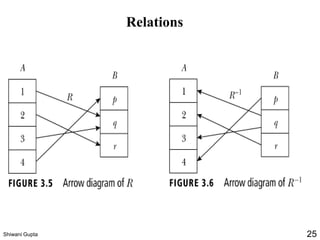
The document discusses relations and their representations. It defines a binary relation as a subset of A×B where A and B are nonempty sets. Relations can be represented using arrow diagrams, directed graphs, and zero-one matrices. A directed graph represents the elements of A as vertices and draws an edge from vertex a to b if aRb. The zero-one matrix representation assigns 1 to the entry in row a and column b if (a,b) is in the relation, and 0 otherwise. The document also discusses indegrees, outdegrees, composite relations, and properties of relations like reflexivity.

1. Relations Digraphs and Lattices
Module 3

2. Relations
If we want to describe a relationship between elements of two
sets A and B, we can use ordered pairs with their first
element taken from A and their second element taken from B.
Since this is a relation between two sets, it is called a binary
relation.
Definition: Let A and B be nonempty sets. A binary relation
from A to B is a subset of AB.
In other words, for a binary relation R we have
R  AB. We use the notation aRb to denote that (a, b)R
and to denote that (a, b)R.
Note: If A=B, we say that R ⊆ AXA is a relation on AShiwani Gupta 2

3. Relations
❑ R can be described in
❑ Roster form
❑ Set-builder form
Shiwani Gupta 3

4. Representing Relations
❑Arrow Diagram
❑Write the elements of A in one column
❑Write the elements B in another column
❑Draw an arrow from an element, a, of A to an element, b, of B,
if (a ,b)  R
❑Here, A = {2,3,5} and B = {7,10,12,30} and R from A into B is
defined as follows: For all a  A and b  B, a R b if and only if
a divides b
❑The symbol → (called an arrow) represents the relation R
Shiwani Gupta 4

5. Representing Relations
Shiwani Gupta 5

6. Representing Relations
❑Directed Graph
❑Let R be a relation on a finite set A
❑Describe R pictorially as follows:
❑For each element of A , draw a small or big dot and label
the dot by the corresponding element of A
❑Draw an arrow from a dot labeled a , to another dot
labeled, b , if a R b .
❑Resulting pictorial representation of R is called the
directed graph representation of the relation R
Shiwani Gupta 6

7. Representing Relations
Shiwani Gupta 7

8. Representing Relations
❑Directed graph (Digraph) representation of R
❑Each dot is called a vertex
❑If a vertex is labeled, a, then it is also called vertex a
❑ An arc from a vertex labeled a, to another vertex, b is
called a directed edge, or directed arc from a to b
❑The ordered pair (A , R) a directed graph, or digraph,
of the relation R, where each element of A is a called
a vertex of the digraph
Shiwani Gupta 8

9. Representing Relations
❑Directed graph (Digraph) representation of R
(Continued)
❑For vertices a and b , if a R b, a is adjacent to b and b is
adjacent from a
❑Because (a, a)  R, an arc from a to a is drawn; because
(a, b)  R, an arc is drawn from a to b. Similarly, arcs are
drawn from b to b, b to c , b to a, b to d, and c to d
❑For an element a  A such that (a, a)  R, a directed edge
is drawn from a to a. Such a directed edge is called a loop
at vertex a
Shiwani Gupta 9

10. Representing Relations
❑Directed graph (Digraph) representation of R
(Continued)
❑Position of each vertex is not important
❑In the digraph of a relation R, there is a directed edge
or arc from a vertex a to a vertex b if and only if a R b
❑Let A ={a ,b ,c ,d} and let R be the relation defined by
the following set:
R = {(a ,a ), (a ,b ), (b ,b ), (b ,c ), (b ,a ), (b ,d ), (c ,d
)}
Shiwani Gupta 10

11. Paths in relations and digraphs
❑A path of length n in R from a to b is a finite sequence
❑Π:a, x1, x2, …, xn-1, b; beginning with a and ending
with b such that aRx1, x1Rx2, …, xn-1Rb
❑A path that begins and ends at the same vertex is cycle
❑A path of length n involves n+1 elements of A, not
necessarily distinct
Shiwani Gupta 11

12. Paths in relations and digraphs
Shiwani Gupta 12

13. Relations
❑ Let A = {a, b, c , d, e , f , g , h, i, j }.
Let R be a relation on A such that the
digraph of R is as shown in Figure
3.14.
❑ Then a, b, c , d, e , f , c , g is a directed
walk in R as a R b,b R c,c R d,d R e, e
R f , f R c, c R g. Similarly, a, b, c , g is
also a directed walk in R. In the walk a,
b, c , d, e , f , c , g , the internal vertices
are b, c , d, e , f , and c , which are not
distinct as c repeats.
❑ This walk is not a path. In the walk a,
b, c , g , the internal vertices are b and c
, which are distinct. Therefore, the
walk a, b, c, g is a path.
Shiwani Gupta 13

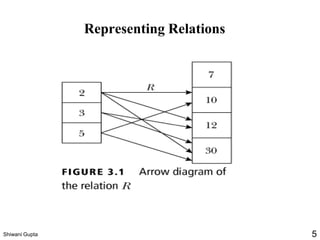
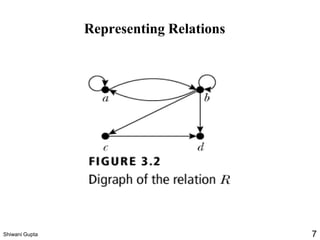
14. Representing Relations
❑Zero-one matrices
If R is a relation from A = {a1, a2, …, am} to B =
{b1, b2, …, bn}, then R can be represented by the zero-one
matrix MR = [mij] with
mij = 1, if (ai, bj)R, and
mij = 0, if (ai, bj)R.
Note that for creating this matrix we first need to list the
elements in A and B in a particular, but arbitrary order.
Shiwani Gupta 14

15. Representing Relations
Example: How can we represent the relation
R = {(2, 1), (3, 1), (3, 2)} as a zero-one matrix?
Solution: The matrix MR is given by










=
11
01
00
RM
Shiwani Gupta 15

16. Representing Relations
The Boolean operations join and meet (you remember?)
can be used to determine the matrices representing the
union and the intersection of two relations, respectively.
To obtain the join of two zero-one matrices, we apply the
Boolean “or” function to all corresponding elements in the
matrices.
To obtain the meet of two zero-one matrices, we apply the
Boolean “and” function to all corresponding elements in the
matrices.
Shiwani Gupta 16

17. Representing Relations
Example: Let the relations R and S be represented by the
matrices










==
011
111
101
SRSR MMM










=
001
110
101
SM
What are the matrices representing RS and RS?
Solution: These matrices are given by










==
000
000
101
SRSR MMM










=
010
001
101
RM
Shiwani Gupta 17

18. Representing Relations
Example: How can we represent the relation
R = {(2, 1), (3, 1), (3, 2)} as a zero-one matrix?
Solution: The matrix MR is given by










=
11
01
00
RM
Shiwani Gupta 18

19. Indegree and outdegree
❑Indegree: Let R is a relation on A and a A, then
indegree of a  A is the no. of b such that bRa i.e. no.
of b|(b,a)  R
❑Outdegree: Let R is a relation on A and a A, then
outdegree of a  A is the no. of b such that aRb i.e.
no. of b|(a,b)  R
❑Eg. A={1,2,3,4,6}=B; aRb iff b is multiple of a
Find matrix relation and relation digraph
Find indegree and outdegree of each vertex
Shiwani Gupta 19

20. Relations
❑Domain and Range of the Relation
❑Let R be a relation from a set A into a set B. Then R ⊆ A x
B. The elements of the relation R tell which element of A
is R-related to which element of B
Shiwani Gupta 20

21. Relations
Shiwani Gupta 21

22. Relations
Shiwani Gupta 22

23. Relations
Shiwani Gupta 23

24. Relations
❑Let A = {1, 2, 3, 4} and B = {p, q, r}. Let R = {(1, q), (2, r ), (3,
q), (4, p)}. Then R−1 = {(q, 1), (r , 2), (q, 3), (p, 4)}
❑To find R−1, just reverse the directions of the arrows
❑D(R) = {1, 2, 3, 4} = Im(R−1), Im(R) = {p, q, r} = D(R−1)
Shiwani Gupta 24

25. Relations
Shiwani Gupta 25

26. Relations
Shiwani Gupta 26

27. Manipulation of Relations
❑ Constructing New Relations from Existing Relations
Shiwani Gupta 27

28. Composite Relations
Definition: Let R be a relation from a set A to a set B and S
a relation from B to a set C. The composite of R and S is
the relation consisting of ordered pairs (a,c), where aA,
cC, and for which there exists an element bB such that
(a,b)R and
(b,c)S. We denote the composite of R and S by
SR.
In other words, if relation R contains a pair (a,b) and
relation S contains a pair (b,c), then SR contains a pair
(a,c).
Shiwani Gupta 28

29. Composite Relations
❑ Example:
❑Consider the relations R and S as given in Figure 3.7.
❑The composition S ◦ R is given by Figure 3.8.
Shiwani Gupta 29

30. Composite Relations
Shiwani Gupta 30

31. Composite Relations
Example: Let D and S be relations on A = {1, 2, 3, 4}.
D = {(a, b) | b = 5 - a} “b equals (5 – a)”
S = {(a, b) | a < b} “a is smaller than b”
D = {(1, 4), (2, 3), (3, 2), (4, 1)}
S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}
SD = {(2, 4), (3, 3), (3, 4), (4, 2), (4, 3),
D maps an element a to the element (5 – a), and afterwards S
maps (5 – a) to all elements larger than (5 – a), resulting in
SD = {(a,b) | b > 5 – a} or SD = {(a,b) | a + b > 5}.
(4, 4)}
Shiwani Gupta 31

32. Connectivity Relation
A relation denoted by R∞ and defined by x R∞y if there is a path of any
length from x to y in R, is called connectivity relation of R
Shiwani Gupta 32

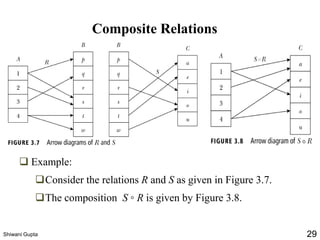
33. Representing Relations Using Matrices
Let us now assume that the zero-one matrices
MA = [aij], MB = [bij] and MC = [cij] represent relations A, B,
and C, respectively.
Remember: For MC = MAMB we have:
cij = 1 if and only if at least one of the terms
(ain  bnj) = 1 for some n; otherwise cij = 0.
In terms of the relations, this means that C contains a pair (xi,
zj) if and only if there is an element yn such that (xi, yn) is in
relation A and
(yn, zj) is in relation B.
Therefore, C = BA (composite of A and B).Shiwani Gupta 33

34. Representing Relations Using Matrices
This gives us the following rule:
MBA = MAMB
In other words, the matrix representing the composite of
relations A and B is the Boolean product of the matrices
representing A and B.
Analogously, we can find matrices representing the powers
of relations:
MRn = MR
[n] (n-th Boolean power).
Shiwani Gupta 34

35. Representing Relations Using Matrices
Example: Find the matrix representing R2, where the
matrix representing R is given by










=
001
110
010
RM
Solution: The matrix for R2 is given by










==
010
111
110
]2[
2 RR
MM
Shiwani Gupta 35

36. Properties of Relations
We will now look at some useful ways to classify relations.
Definition: A relation R on a set A is called reflexive if (a, a)R for every element
aA.
Are the following relations on {1, 2, 3, 4} reflexive?
R = {(1, 1), (1, 2), (2, 3), (3, 3), (4, 4)} No.
R = {(1, 1), (2, 2), (2, 3), (3, 3), (4, 4)}
Yes.
R = {(1, 1), (2, 2), (3, 3)}
No.
Definition: A relation on a set A is called irreflexive if (a, a)R for every element
aA.
Note: Δ ⊆ R if R is reflexive relation on A
Δ ∩ R= Ø if relation R is irreflexive
Relation R may be either reflexive or irreflexive but not both
Diagonal Relation / Equality Relation : Δ = {(a, a) for every element aA}.
aRa for every a A but for any b A
Shiwani Gupta 36

37. Representing Relations
What do we know about the matrices representing a
relation on a set (a relation from A to A) ?
They are square matrices.
What do we know about matrices representing reflexive
relations?
All the elements on the diagonal of such matrices Mref must
be 1s.




















=
1
.
.
.
1
1
refM
Shiwani Gupta 37

38. Properties of Relations
Definitions:
A relation R on a set A is called symmetric if (b, a)R whenever (a,
b)R for all a, bA.
A relation R on a set A is called antisymmetric if a = b whenever (a,
b)R and (b, a)R.
A relation R on a set A is called asymmetric if (a, b)R implies that (b,
a)R for all (a, b)A.
A relation R on a set A is called not symmetric if (a, b)R but (b,
a)R for some (a, b)A.
Note: R-1=R for symmetric relation
R-1 ≠ R for not symmetric relation
R-1 ∩ R= Ø for asymmetric relation
R-1 ∩ R ⊆ Δ for anti symmetric relationShiwani Gupta 38

39. Representing Relations
What do we know about the matrices representing
symmetric relations?
These matrices are symmetric, that is, MR = (MR)t.












=
1101
1001
0010
1101
RM
symmetric matrix,
symmetric relation.












=
0011
0011
0011
0011
RM
non-symmetric matrix,
non-symmetric relation.
Shiwani Gupta 39

40. Properties of Relations
Are the following relations on {1, 2, 3, 4}
symmetric, antisymmetric, or asymmetric?
R = {(1, 1), (1, 2), (2, 1), (3, 3), (4, 4)} symmetric
R = {(1, 1)} sym. and
antisym.
R = {(1, 3), (3, 2), (2, 1)} antisym. and
asym.
R = {(4, 4), (3, 3), (1, 4)} antisym.
Shiwani Gupta 40

41. Properties of Relations
Definition: A relation R on a set A is called transitive if whenever
(a, b)R and (b, c)R, then (a, c)R for a, b, cA.
Are the following relations on {1, 2, 3, 4} transitive?
R = {(1, 1), (1, 2), (2, 2), (2, 1), (3, 3)} Yes.
R = {(1, 3), (3, 2), (2, 1)} No.
R = {(2, 4), (4, 3), (2, 3), (4, 1)} No.
Shiwani Gupta 41

42. Equivalence Relation
Shiwani Gupta 42

43. Equivalence Relation
Shiwani Gupta 43

44. Equivalence Relation
Shiwani Gupta 44

45. Example 3.1.26 continued
Equivalence Relation
Shiwani Gupta 45

46. Equivalence Relation
Shiwani Gupta 46

47. Example 3.1.27 continued
Equivalence Relation
Shiwani Gupta 47

48. Equivalence Relation
Shiwani Gupta 48

49. Example 3.1.31 continued
Equivalence Relation
Shiwani Gupta 49

50. Equivalence Relation
Shiwani Gupta 50

51. Example 3.1.32 continued
Equivalence Relation
Shiwani Gupta 51

52. Equivalence Classes and partitions
Shiwani Gupta 52

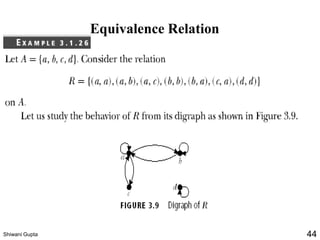
53. Equivalence Classes
Definition: Let R be an equivalence relation on a set A.
The set of all elements that are related to an element a of A
is called the equivalence class
of a.
The equivalence class of a with respect to R is denoted by
[a]R.
When only one relation is under consideration, we will
delete the subscript R and write [a] for this equivalence
class.
If b[a]R, b is called a representative of this equivalence
class.
Shiwani Gupta 53

54. Equivalence Classes
Example: In the previous example (strings of identical
length), what is the equivalence class of the word mouse,
denoted by [mouse] ?
Solution: [mouse] is the set of all English words containing
five letters.
For example, ‘horse’ would be a representative of this
equivalence class.
Shiwani Gupta 54

55. Partition of sets
❑ Example: Let A denote the set
of the lowercase English
alphabet. Let B be the set of
lowercase consonants and C
be the set of lowercase
vowels. Then B and C are
nonempty, B ∩ C = , and A
= B ∪ C. Thus, {B, C} is a
partition of A.
❑ Let A be a set and let {A1, A2,
A3, A4, A5} be a partition of A.
Corresponding to this
partition, a Venn diagram,
can be drawn, Figure 3.13
Shiwani Gupta 55

56. Equivalence Classes
Theorem: Let R be an equivalence relation on a set A. The
following statements are equivalent:
❑ aRb
❑ [a] = [b]
❑ [a]  [b]  
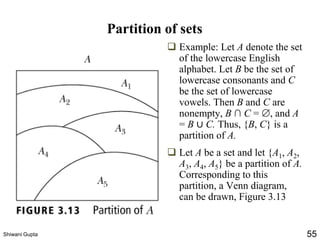
Definition: A partition of a set S is a collection of disjoint
nonempty subsets of S that have S as their union. In other words,
the collection of subsets Ai, iI, forms a partition of S if and only
if
(i) Ai   for iI
❑ Ai  Aj = , if i  j
❑ iI Ai = S
Shiwani Gupta 56

57. Equivalence Classes
Examples: Let S be the set {u, m, b, r, o, c, k, s}.
Do the following collections of sets partition S ?
{{m, o, c, k}, {r, u, b, s}} yes.
{{c, o, m, b}, {u, s}, {r}} no (k is missing).
{{b, r, o, c, k}, {m, u, s, t}} no (t is not in S).
{{u, m, b, r, o, c, k, s}} yes.
{{b, o, o, k}, {r, u, m}, {c, s}} yes ({b,o,o,k} = {b,o,k}).
{{u, m, b}, {r, o, c, k, s}, } no ( not allowed).
Shiwani Gupta 57

58. Equivalence Classes
Theorem: Let R be an equivalence relation on a
set S. Then the equivalence classes of R form a partition of
S. Conversely, given a partition
{Ai | iI} of the set S, there is an equivalence relation R that
has the sets Ai, iI, as its equivalence classes.
Shiwani Gupta 58

59. Example: Equivalence Classes
Let us assume that Frank, Suzanne and George live in
Boston, Stephanie and Max live in Lübeck, and Jennifer
lives in Sydney.
Let R be the equivalence relation {(a, b) | a and b live in
the same city} on the set P = {Frank, Suzanne, George,
Stephanie, Max, Jennifer}.
Then R = {(Frank, Frank), (Frank, Suzanne),
(Frank, George), (Suzanne, Frank), (Suzanne, Suzanne),
(Suzanne, George), (George, Frank),
(George, Suzanne), (George, George), (Stephanie,
Stephanie), (Stephanie, Max), (Max, Stephanie),
(Max, Max), (Jennifer, Jennifer)}.
Shiwani Gupta 59

60. Equivalence Classes
Then the equivalence classes of R are:
{{Frank, Suzanne, George}, {Stephanie, Max}, {Jennifer}}.
This is a partition of P.
The equivalence classes of any equivalence relation R
defined on a set S constitute a partition of S, because every
element in S is assigned to exactly one of the equivalence
classes.
Shiwani Gupta 60

61. Example: Equivalence Classes
Let R be the relation
{(a, b) | a  b (mod 3)} on the set of integers.
Is R an equivalence relation?
Yes, R is reflexive, symmetric, and transitive.
What are the equivalence classes of R ?
{{…, -6, -3, 0, 3, 6, …},
{…, -5, -2, 1, 4, 7, …},
{…, -4, -1, 2, 5, 8, …}}
Shiwani Gupta 61

62. ❑Quotient Set: A set denoted by A/R is the collection
of all distinct and disjoint sets of equivalence classes,
induced by an equivalence relation R
❑Quotient set is a partition of A
❑Circular Set: A relation R on set A is said to be
circular if aRb and bRc ⇒ cRa
Shiwani Gupta 62

63. Reflexive closure
Smallest reflexive relation R1 = Δ U R
❑Let R be a relation on set A and R is not reflexive then
a smallest reflexive relation on A is said to be reflexive
closure of R if it contains R
If R is a reflexive relation, then reflexive closure of R
is itself
Shiwani Gupta 63

64. Symmetric closure
Smallest symmetric relation R1 = R-1 U R
❑Let R be a relation on set A and R is not symmetric then
a smallest symmetric relation on A is said to be
symmetric closure of R if it contains R
If R is symmetric, then symmetric closure of R is itself
Shiwani Gupta 64

65. Transitive closure
Transitive closure of R = R ∞ i.e connectivity relation
❑Let R be a relation on set A and R is not transitive then a
smallest transitive relation on A is said to be transitive
closure of R if it contains R
If R is transitive, then transitive closure of R is itself
Transitive closure of non transitive relation can be found
by Warshall’s algorithm
Shiwani Gupta 65

66. Antisymmetric Relation
Eg. 1
Eg. 2
Shiwani Gupta 66

67. Partial Order Relation
Shiwani Gupta 67

68. Dual of poset
Shiwani Gupta 68

69. Linearly Ordered Sets
Note: In a poset, every pair of elements need not be comparable
Eg. (R, ≤) is linearly ordered set whereas (Z+, |) is not
Shiwani Gupta 69

70. Partially Ordered Sets
❑ Digraphs of Posets
❑ Because any partial order is also a
relation, a digraph representation of
partial order may be given.
❑ Example: On the set S = {a, b, c},
consider the relation R =
{(a, a), (b, b), (c , c ), (a, b)}.
❑ From the directed graph it follows that
the given relation is reflexive and
transitive.
❑ This relation is also antisymmetric
because there is a directed edge from a
to b, but there is no directed edge from b
to a.
Shiwani Gupta 70

71. Partially Ordered Sets
❑Digraphs of Posets
❑Let S = {1, 2, 3, 4, 6, 12}.
Consider the divisibility
relation on S, which is a
partial order
❑A digraph of this poset is as
shown in Figure 3.20
Shiwani Gupta 71

72. Partially Ordered Sets
Shiwani Gupta 72

73. Partially Ordered Sets
❑Closed Path
❑On the set S = {a, b, c } consider
the relation R = {(a, a), (b, b), (c ,
c ), (a, b), (b, c ), (c , a)}
❑The digraph of this relation is given
in Figure 3.21
❑In this digraph, a, b, c , a form a
closed path. Hence, the given
relation is not a partial order
relation
Shiwani Gupta 73

74. Hasse Diagram
The digraph of a partial ordered relation can be
simplified and is called as Hasse Diagram.
When the partial order is a total order, its hasse diagram
is a straight line and the corresponding poset is called
chain
Shiwani Gupta 74

75. Hasse Diagram
Shiwani Gupta 75

76. Hasse Diagram
❑Let S = {1, 2, 3}. Then P(S)
= {, {1}, {2}, {3}, {1, 2},
{2, 3}, {1, 3}, S}
❑(P(S),≤) is a poset, where ≤
denotes the set inclusion
relation
❑Draw the digraph of this
inclusion relation (see Figure
3.23). Place the vertex A
above vertex B if B ⊂ A.
Now follow steps (2), (3),
and (4)
Shiwani Gupta 76

77. ❑Let S = {1, 2, 3}. Then P(S) =
{, {1}, {2}, {3}, {1, 2}, {2, 3},
{1, 3}, S}
❑Now (P(S),≤) is a poset, where ≤
denotes the set inclusion relation.
The poset diagram of (P(S),≤) is
shown in Figure 3.22
Hasse Diagram
Shiwani Gupta 77

78. ❑Quasi Order: A relation R on A is called quasi order if
it is transitive and irreflexive
❑Poset isomorphism: If f:A→A’ (one-one
correspondence) is an isomorphism then (A,≤) and
(A’,≤’) are known as isomorphic posets
A={1,2,3,5,6,10,15,30}
P(S)=A’={ϕ,{e},{f},{g},{e,f},{f,g},{e,g},{e,f,g}}
Shiwani Gupta 78

79. Note: The greatest element of a poset is denoted by ‘I’ or’1’ is called
‘unit element’
The least element of a poset is denoted by 0 is called ‘zero
element’
Minimal and Maximal Elements
Shiwani Gupta 79

80. ❑Consider the poset (S,≤), where S =
{2, 4, 5, 10, 15, 20} and the partial
order ≤ is the divisibility relation
❑In this poset, there is no element b ∈
S such that b  5 and b divides 5.
(That is, 5 is not divisible by any
other element of S except 5). Hence,
5 is a minimal element. Similarly, 2
is a minimal element
Hasse Diagram
Shiwani Gupta 80

81. ❑10 is not a minimal element because
2 ∈ S and 2 divides 10. That is, there
exists an element b ∈ S such that b <
10. Similarly, 4, 15, and 20 are not
minimal elements
❑2 and 5 are the only minimal
elements of this poset. Notice that 2
does not divide 5. Therefore, it is not
true that 2 ≤ b, for all b ∈ S, and so 2
is not a least element in (S,≤).
Similarly, 5 is not a least element.
This poset has no least element
Hasse Diagram
Shiwani Gupta 81

82. ❑There is no element b ∈ S such that b
15, b > 15, and 15 divides b. That is,
there is no element b ∈ S such that 15
< b. Thus, 15 is a maximal element.
Similarly, 20 is a maximal element.
❑10 is not a maximal element because
20 ∈ S and 10 divides 20. That is,
there exists an element b ∈ S such
that 10 < b. Similarly, 4 is not a
maximal element.
Figure 3.24
Hasse Diagram
Shiwani Gupta 82

83. ❑20 and 15 are the only
maximal elements of this
poset
❑10 does not divide 15, hence
it is not true that b ≤ 15, for
all b ∈ S, and so 15 is not a
greatest element in (S,≤)
❑This poset has no greatest
element
Figure 3.24
Hasse Diagram
Shiwani Gupta 83

84. Lattice
Shiwani Gupta 84

85. Lattice
Shiwani Gupta 85

86. Lattice
Shiwani Gupta 86

87. Lattice
Shiwani Gupta 87

88. Lattice
Shiwani Gupta 88

89. Lattice
Shiwani Gupta 89

90. Lattice
A lattice L is said to be bounded if it has greatest element
1 and least element 0
If L is bounded lattice then for all a ∈ A, 0≤ a≤ 1
aV0=a, a ∧0=0, aV1=1, a ∧ 1=a
Let (L,≤) be the lattice, a nonempty subset S of L is called
sublattice of L if ∀ a,b ∈S, aVb, a ∧b ∈S
Shiwani Gupta 90

91. ❑Non-distributive Lattice
❑Because a ∧ (b ∨ c ) = a ∧ 1 = a = 0
= 0 ∨ 0 = (a ∧ b) ∨ (a ∧ c ), this is
not a distributive lattice
Lattice
1
a
b
c
0
A Lattice is non distributive iff it contains
a sublattice which is isomorphic to one of
the aboveShiwani Gupta 91

92. Complemented Lattice
A Lattice is said to be complemented if it is bounded and
every element of L has a complement.
Complement of each element of bounded, distributive
lattice is unique.
Shiwani Gupta 92

93. ❑Modular Lattice: A lattice is said to be modular if for
all a,b,c, a≤c→aV(b ∧c)=(aVb) ∧c
Shiwani Gupta 93

94. Boolean Algebra
Boolean Algebra is a lattice which is bounded, distributive and
complementedShiwani Gupta 94

95. Properties of Boolean Algebra
❑Every Boolean Algebra is isomorphic to the Boolean
Algebra (P(S), ⊆), where S is some set
❑Every Boolean Algebra must have elements of the
form 2n
Shiwani Gupta 95

96. Application: Relational Database
❑In a relational database system, tables are considered
as relations
❑A table is an n-ary relation, where n is the number of
columns in the tables
❑The headings of the columns of a table are called
attributes, or fields, and each row is called a record
❑The domain of a field is the set of all (possible)
elements in that column
Shiwani Gupta 96

97. n-ary Relations
In order to study an interesting application of relations,
namely databases, we first need to generalize the concept
of binary relations to n-ary relations.
Definition: Let A1, A2, …, An be sets. An n-ary relation
on these sets is a subset of A1A2…An.
The sets A1, A2, …, An are called the domains of the
relation, and n is called its degree.
Shiwani Gupta 97

98. n-ary Relations
Example:
Let R = {(a, b, c) | a = 2b  b = 2c with a, b, cN}
What is the degree of R?
The degree of R is 3, so its elements are triples.
What are its domains?
Its domains are all equal to the set of integers.
Is (2, 4, 8) in R?
No.
Is (4, 2, 1) in R?
Yes.
Shiwani Gupta 98

99. Databases and Relations
Let us take a look at a type of database representation that is
based on relations, namely the relational data model.
A database consists of n-tuples called records, which are
made up of fields.
These fields are the entries of the n-tuples.
The relational data model represents a database as an n-ary
relation, that is, a set of records.
Shiwani Gupta 99

100. Databases and Relations
Example: Consider a database of students, whose records
are represented as 4-tuples with the fields Student Name, ID
Number, Major, and GPA:
R = {(Ackermann, 231455, CS, 3.88),
(Adams, 888323, Physics, 3.45),
(Chou, 102147, CS, 3.79),
(Goodfriend, 453876, Math, 3.45),
(Rao, 678543, Math, 3.90),
(Stevens, 786576, Psych, 2.99)}
Relations that represent databases are also called tables,
since they are often displayed as tables.
Shiwani Gupta 100