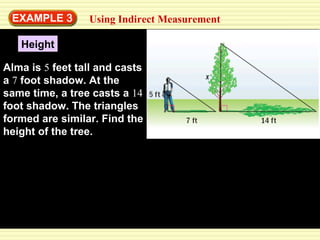
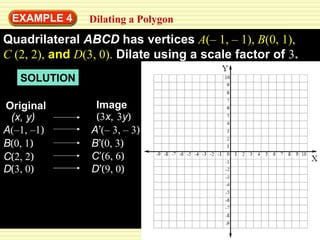
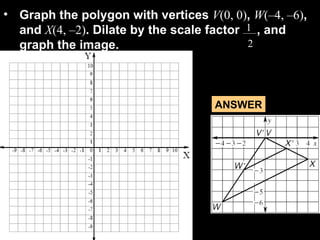
This document discusses transformations in geometry, including reflections, similarities, dilations, and their applications. It provides examples of determining if figures are reflections or similar, using proportions to find unknown side lengths, and dilating polygons by multiplying the coordinates by a scale factor. Key points covered are defining similar polygons as those with the same shape but different sizes, using proportions to solve similarity problems, and dilating figures by multiplying the original coordinates by the scale factor.

1. Lesson 8.7 , For use with pages 439-444 Tell whether the figure is a reflection in the line shown? 1. 2.

2. Lesson 8.7 , For use with pages 439-444 Tell whether the figure is a reflection in the line shown? ANSWER no 1. ANSWER yes 2.

3. 8.8 Similarity and Dilations

4. Essential Questions What are the similarities and differences among transformations? How are the principles of transformational geometry used in art, architecture and fashion? What are the applications for transformations?

5. Similar Polygons Similar polygons have the same shape but can be different sizes. The symbol ~ means “is similar to.”

7. EXAMPLE 1 Identifying Similar Polygons STEP 1 Decide whether corresponding angles are congruent. Each angle measures 90 . Tell whether the television screens are similar. A E B F C G D H

8. STEP 2 Decide whether corresponding side lengths are proportional. EXAMPLE 1 Identifying Similar Polygons 30 inches 18 inches 40 inches 24 inches = ? 5 3 = 5 3 ANSWER Yes, quadrilateral ABCD ~ quadrilateral EFGH .

9. SOLUTION EXAMPLE 2 Standardized Test Practice Corresponding side lengths are proportional. Write a proportion. Substitute given values. Solve the proportion. KL NP = LM PQ KL 12 M = 10M 5 M KL = 24

10. EXAMPLE 3 Using Indirect Measurement Height Alma is 5 feet tall and casts a 7 foot shadow. At the same time, a tree casts a 14 foot shadow. The triangles formed are similar. Find the height of the tree.

11. SOLUTION EXAMPLE 3 Using Indirect Measurement You can use a proportion to find the height of the tree. Write a proportion. Substitute given values. Solve the proportion. Tree’s height Alma’s height = Length of tree’s shadow Length of Alma’s shadow x feet 5 feet = 14feet 7 feet x 10 = ANSWER The tree is 10 feet tall.

12. Dilation Stretches or shrinks a figure The image created by a dilation is similar to the original figure. Scale factor : of a dilation is the ratio of a side length after the dilation to the corresponding side length before the dilation.

14. Dilations National Library of Virtual Manipulatives Geometry 6-8 Transformations- Dilations

16. Dimensions can be scaled “UP” or scaled “DOWN” – as stated before. To scale up, means you would multiply by a number that is _______________. To scale down, you would multiply by a number that is _________________ greater than one. less than one

17. EXAMPLE 4 Dilating a Polygon Quadrilateral ABCD has vertices A (– 1, – 1), B (0, 1), C (2, 2), and D (3, 0). Dilate using a scale factor of 3 . SOLUTION Original Image (x, y) A (–1, –1 ) B ( 0, 1 ) C ( 2, 2 ) D ( 3, 0 ) ( 3 x , 3 y ) A ’ (– 3, – 3 ) B ’ ( 0, 3 ) C ’ ( 6, 6 ) D ’ ( 9, 0 )

18. EXAMPLE 4 Dilating a Polygon Quadrilateral ABCD has vertices A (– 1, – 1), B (0, 1), C (2, 2), and D (3, 0). Dilate using a scale factor of 3 . SOLUTION Graph the quadrilateral. Find the coordinates of the vertices of the image. Graph the image of the quadrilateral. Original Image (x, y) A (–1, –1 ) B ( 0, 1 ) C ( 2, 2 ) D ( 3, 0 ) ( 3 x , 3 y ) A ’ (– 3, – 3 ) B ’ ( 0, 3 ) C ’ ( 6, 6 ) D ’ ( 9, 0 )

19. Graph the polygon with vertices V (0, 0) , W (–4, –6) , and X (4, –2) . Dilate by the scale factor , and graph the image. 1 2 ANSWER

20. Homework Page 450 #1-8, 12, 14 Number 12: D (2,6) Number 14: k =2