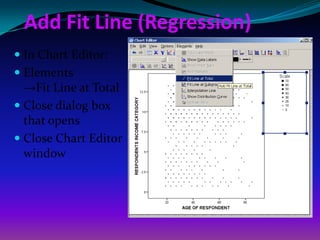
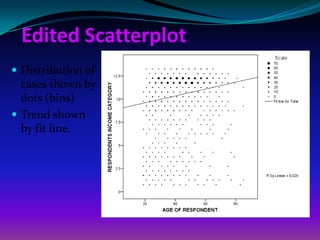
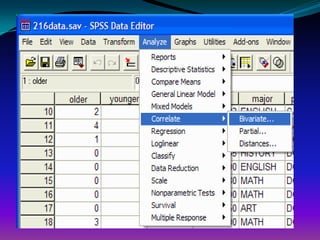
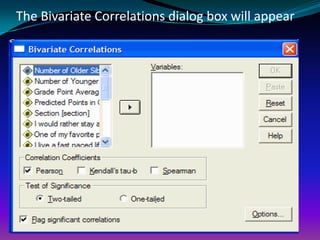
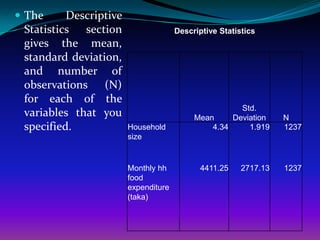
This document provides an overview of correlation analysis procedures in SPSS, including bivariate correlation, partial correlation, and distance measures. It discusses interpreting correlation coefficients and significance values. Scatterplots are recommended to check assumptions before correlation. Hands-on exercises are included to find correlations between variables while controlling for other variables.

1. Srinivasulu Rajendran
Centre for the Study of Regional Development (CSRD)
Jawaharlal Nehru University (JNU)
New Delhi
India
r.srinivasulu@gmail.com

2. Objective of the session
To understand
CORRELATION

3. 1. What is the procedure to
perform Correlation &
Regression?
2. How do we interpret results?

4. Identify the relationship between variables that
we want to perform Scatter plot for outliers and
type of relationship
 Monthly HH food Expenditure and HHSIZE

5. Interpreting Correlation Coefficient r
 strong correlation: r > .70 or r < –.70
 moderate correlation: r is between .30 & .70
or r is between –.30 and –.70
 weak correlation: r is between 0 and .30
or r is between 0 and –.30 .

6. GENERATE A SCATTERPLOT TO SEE
THE RELATIONSHIPS
Go to Graphs → Legacy dialogues→ Scatter/Dot → Simple
Click on DEPENDENT “mfx”. and move it to the Y-Axis
Click on the “hhsize”. and move it to the X-Axis
Click OK

7. Scatterplot might not look promising at first
Double click on chart to open a CHART EDIT window

8. use Options →Bin Element Simply CLOSE this box.
Bins are applied automatically.

9. BINS
Dot size now
shows
number of
cases with
each pair of
X, Y values
DO NOT CLOSE CHART EDITOR YET!

10. Add Fit Line (Regression)
 In Chart Editor:
 Elements
→Fit Line at Total
 Close dialog box
that opens
 Close Chart Editor
window

11. Edited Scatterplot
 Distribution of
cases shown by
dots (bins)
 Trend shown
by fit line.

12. Type of Correlation
 Bivariate Correlations.
 Partial Correlations
 Distances

13. BIVARIATE CORRELATIONS
 In Bivariate Correlations, the relationship between two
variables is measured. The degree of relationship (how
closely they are related) could be either positive or
negative. The maximum number could be either +1
(positive) or -1 (negative). This number is the
correlation coefficient. A zero correlation indicates no
relationship. Remember that you will want to perform
a scatter plot before performing the correlation (to see
if the assumptions have been met.)

14. Objective
 We are interested in whether an monthly HH food
expenditure was correlated with hhsize.

15. Step 1

17. The Bivariate Correlations dialog box will appear

18. Right
List of
arrow
Variables
button to
add
selected
variable(s)

19. Step 2

20.  Select one of the variables that you want to correlate by
clicking on it in the left hand pane of the Bivariate
Correlations dialog box i.e mfx and hhsize
 Check the type of correlation coefficients that you require
(Pearson for parametric, and Kendall’s tau-b and Spearman
for non-parametric).
 Select the appropriate Test: Pearson’s correlation coefficient
assumes that each pair of variables is bivariate normal and
it is a measure of linear association. Two variables can be
perfectly related, but if the relationship is not linear,
Pearson’s correlation coefficient is not an appropriate
statistic for measuring their association.
 Test of Significance: You can select two-tailed or one-tailed
probabilities. If the direction of association is known in
advance, select One-tailed. Otherwise, select Two-tailed.

21.  Flag significant correlations. Correlation coefficients
significant at the 0.05 level are identified with a single
asterisk, and those significant at the 0.01 level are
identified with two asterisks.
 Click on the Options… button to select statistics, and
select Means and SD and control the missing value by
clicking “Exclude Cases pairwise.

22. Click on the Continue button.

23. Step 3

24. Click the OK button in
the Bivariate
Correlations dialog box
to run the analysis. The
output will be displayed
in a separate SPSS
Viewer window.

25. SPSS Output of Correlation Matrix

26.  The Descriptive
Statistics section Descriptive Statistics
gives the mean,
standard deviation,
and number of
observations (N)
for each of the
Std.
variables that you Mean Deviation N
specified. Household 4.34 1.919 1237
size
Monthly hh 4411.25 2717.13 1237
food
expenditure
(taka)

27. The correlations table displays Pearson
correlation coefficients, significance values, Correlations
and the number of cases with non-missing
values (N).
Monthl
y hh
The values of the correlation coefficient
food
range from -1 to 1.
expend
Househol iture
The sign of the correlation coefficient
d size (taka)
indicates the direction of the relationship Household Pearson 1 .608
**
(positive or negative). size Correlation
Sig. (1- .000
The absolute value of the correlation
tailed)
coefficient indicates the strength, with
N 1237 1237
larger absolute values indicating stronger
relationships. **
Monthly hh Pearson .608 1
food Correlation
The correlation coefficients on the main
expenditure Sig. (1- .000
diagonal are always 1, because each variable
(taka) tailed)
has a perfect positive linear relationship with
itself. N 1237 1237

28.  The significance of each
correlation coefficient is also
Correlations
displayed in the correlation
table.
Monthl
y hh
 The significance level (or p- food
value) is the probability of expend
obtaining results as extreme Househol iture
d size (taka)
as the one observed. If the **
Household Pearson 1 .608
significance level is very small size Correlation
(less than 0.05) then the Sig. (1- .000
correlation is significant and tailed)
the two variables are linearly N 1237 1237
related. If the significance
**
level is relatively large (for Monthly hh Pearson .608 1
example, 0.50) then the food Correlation
correlation is not significant expenditure Sig. (1- .000
and the two variables are not (taka) tailed)
linearly related. N 1237 1237

29. Partial Correlations
 The Partial Correlations procedure computes partial
correlation coefficients that describe the linear
relationship between two variables while controlling
for the effects of one or more additional variables.
Correlations are measures of linear association. Two
variables can be perfectly related, but if the
relationship is not linear, a correlation coefficient is
not a proper statistic to measure their association.

30. Step 1

31. How to perform Partial Correl: SPSS
Analyze –> Correlate –> Partial...

32. You will be presented with the “Partial Correlations" dialogue box:

33. Step 2

34.  Click right
click on
variables and
select “Display
Variable”
 Click “Sort
Alphabetically
“

35. Step 3

37. Step 4

38.  Select one of the
variables that you want
to correlate by clicking
on it in the left hand
pane of the Bivariate
Correlations dialog
box i.e mfx and hhsize
 In this case, we can see
the correlation
between monthly HH
food expenditure and
household size when
head of education
maintain constant.
 Test of Significance:
You can select two-
tailed or one-tailed
probabilities. If the
direction of
association is known
in advance, select
One-tailed. Otherwise,
select Two-tailed.

39.  Flag significant
correlations.
Correlation
coefficients
significant at
the 0.05 level
are identified
with a single
asterisk, and
those
significant at
the 0.01 level
are identified
with two
asterisks.
 Click OK to get
results

40. Step 5

41. As we can see, the Correlations
positive
Monthl
correlation y hh
food
between mfx and expend
Househol iture
hhsize when Control Variables
(sum) head_edu Household size Correlation
d size (taka)
1.000 .606
hh_edu is Significance . .000
(1-tailed)
maintained
constant is df 0 1232
significant at 1% Monthly hh
food
Correlation .606 1.000
level (p > 0.00) expenditure
(taka)
Significance
(1-tailed)
.000 .
df 1232 0

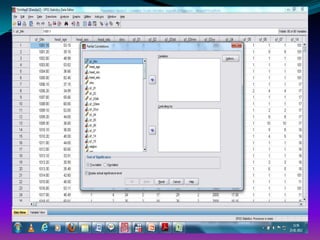
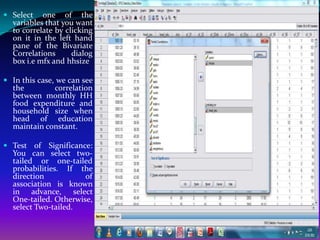
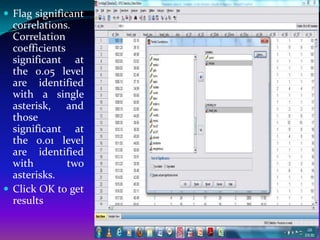
42. Hands-on Exercises
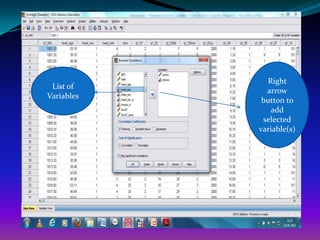
 Find out the correlation relationship between per
capita total monthly expenditure and household size
and identify the nature of relationship and define the
reasons?
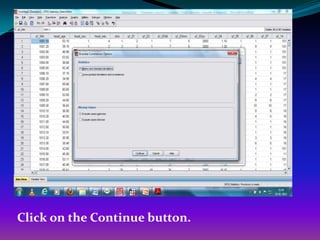
 Find out the correlation relationship between per
capita total monthly expenditure and household size
by controlling the village those who have adopted
technology and not adopted tech?
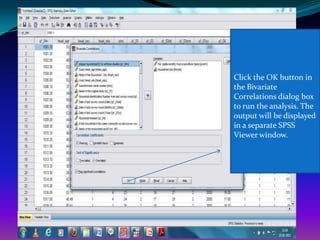
 Find out the correlation relationship between per
capita food expenditure and non-food expenditure by
controlling district effect? [Hint: it is two tail why?]

43. Distances
 This procedure calculates any of a wide variety of
statistics measuring either similarities or
dissimilarities (distances), either between pairs of
variables or between pairs of cases. These similarity or
distance measures can then be used with other
procedures, such as factor analysis, cluster analysis, or
multidimensional scaling, to help analyze complex
data sets.