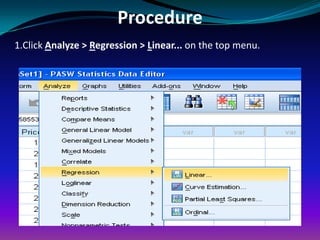
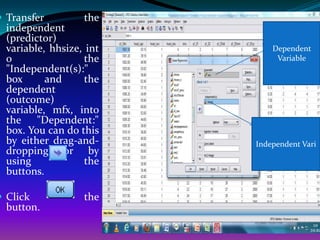
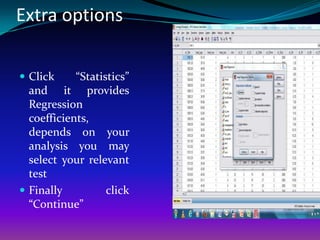
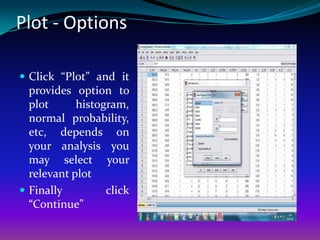
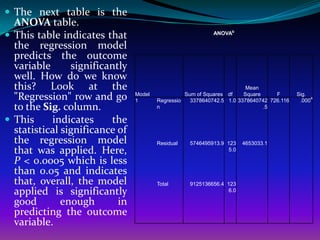
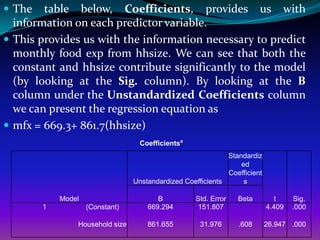
The document discusses using linear regression analysis in SPSS to analyze the relationship between household size (independent variable) and monthly per capita household expenditure (dependent variable). It outlines the steps to perform the regression analysis in SPSS, including selecting variables, interpreting output tables like the model summary, ANOVA table, and coefficients table. The analysis finds that household size significantly influences monthly expenditure, with expenditure increasing by about 862 taka for each additional household member.

1. Srinivasulu Rajendran
Centre for the Study of Regional Development (CSRD)
Jawaharlal Nehru University (JNU)
New Delhi
India
r.srinivasulu@gmail.com

2. Objective of the session
To understand How
HHsize influences the
monthly per capita
total expenditure of the
households based OLS

3. 1. What is the procedure to
perform Regression?
2. How do we interpret results?
4. What are procedure available
for estimating poverty line and
Poverty rate and how to do with
Econometric software

4. Identify the relationship between variables that
we want to perform Scatter plot for outliers and
type of relationship
 Monthly HH food Expenditure and HHSIZE

5. Linear Regression Analysis using
SPSS

6. Objectives
 Regression analysis is the next step up after
correlation; it is used when we want to predict the
value of a variable based on the value of another
variable. In this case, the variable we are using to
predict the other variable's value is called the
independent variable or sometimes the predictor
variable. The variable we are wishing to predict is
called the dependent variable or sometimes the
outcome variable.

7. Assumption
 Variables are approximately normally distributed
(see Testing for Normality guide).
 There is a linear relationship between the two
variables.
 There are classical assumption ……..

8. Step 1

9. Procedure
1.Click Analyze > Regression > Linear... on the top menu.

10. You will be presented with the following dialog box:

11. Step 2

12.  Transfer the
independent
(predictor)
variable, hhsize, int Dependent
o the Variable
"Independent(s):"
box and the
dependent
(outcome)
variable, mfx, into
the "Dependent:"
box. You can do this
by either drag-and- Independent Vari
dropping or by
using the
buttons.
 Click the
button.

13. Step 2

14. Extra options
 Click “Statistics”
and it provides
Regression
coefficients,
depends on your
analysis you may
select your relevant
test
 Finally click
“Continue”

15. Plot - Options
 Click “Plot” and it
provides option to
plot histogram,
normal probability,
etc, depends on
your analysis you
may select your
relevant plot
 Finally click
“Continue”

16. Click “OK”
to get results
in the output
viewer

17. Output of Linear Regression
Analysis

18.  SPSS will generate quite a
few tables in its results
section for a linear
regression.
 In this session, we are going
to look at the important Model Summary
tables Model Summary
table.
 This table provides the R
and R2 value. The R value is
0.608, which represents the
Adjusted R Std. Error of
simple correlation Model R R Square Square the Estimate
a
and, therefore, indicates a 1 .608 .370 .370 2157.08
high degree of correlation.
The R2 value indicates how
much of the dependent
variable, monthly HH food
exp, can be explained by the
independent
variable, hhsize. In this
case, 37.0% can be
explained.

19.  The next table is the
ANOVA table.
 This table indicates that ANOVAb
the regression model
predicts the outcome
variable significantly
well. How do we know
this? Look at the Mean
"Regression" row and go Model
1 Regressio
Sum of Squares df Square F
3378640742.5 1.0 3378640742 726.116
Sig.
.000
a
to the Sig. column. n .5
 This indicates the
statistical significance of
the regression model Residual 5746495913.9 123 4653033.1
that was applied. Here, 5.0
P < 0.0005 which is less
than 0.05 and indicates
that, overall, the model Total 9125136656.4 123
applied is significantly 6.0
good enough in
predicting the outcome
variable.

20.  The table below, Coefficients, provides us with
information on each predictor variable.
 This provides us with the information necessary to predict
monthly food exp from hhsize. We can see that both the
constant and hhsize contribute significantly to the model
(by looking at the Sig. column). By looking at the B
column under the Unstandardized Coefficients column
we can present the regression equation as
 mfx = 669.3+ 861.7(hhsize)
Coefficientsa
Standardiz
ed
Coefficient
Unstandardized Coefficients s
Model B Std. Error Beta t Sig.
1 (Constant) 669.294 151.807 4.409 .000
Household size 861.655 31.976 .608 26.947 .000

21. Interpretation
 If HHSIZE goes up by a member or individual, the average
monthly HH food expenditure (mfx) goes up by about 862
taka. The intercept value of about 669 taka tells us that if
hhsize were zero, mfx would be about 669 taka. The r 2
value of 0.37 means approximately 37 percent
 of the variation in the mfx is explained by variation
 in the hhsize.
Coefficientsa
Standardiz
ed
Coefficient
Unstandardized Coefficients s
Model B Std. Error Beta t Sig.
1 (Constant) 669.294 151.807 4.409 .000
Household size 861.655 31.976 .608 26.947 .000