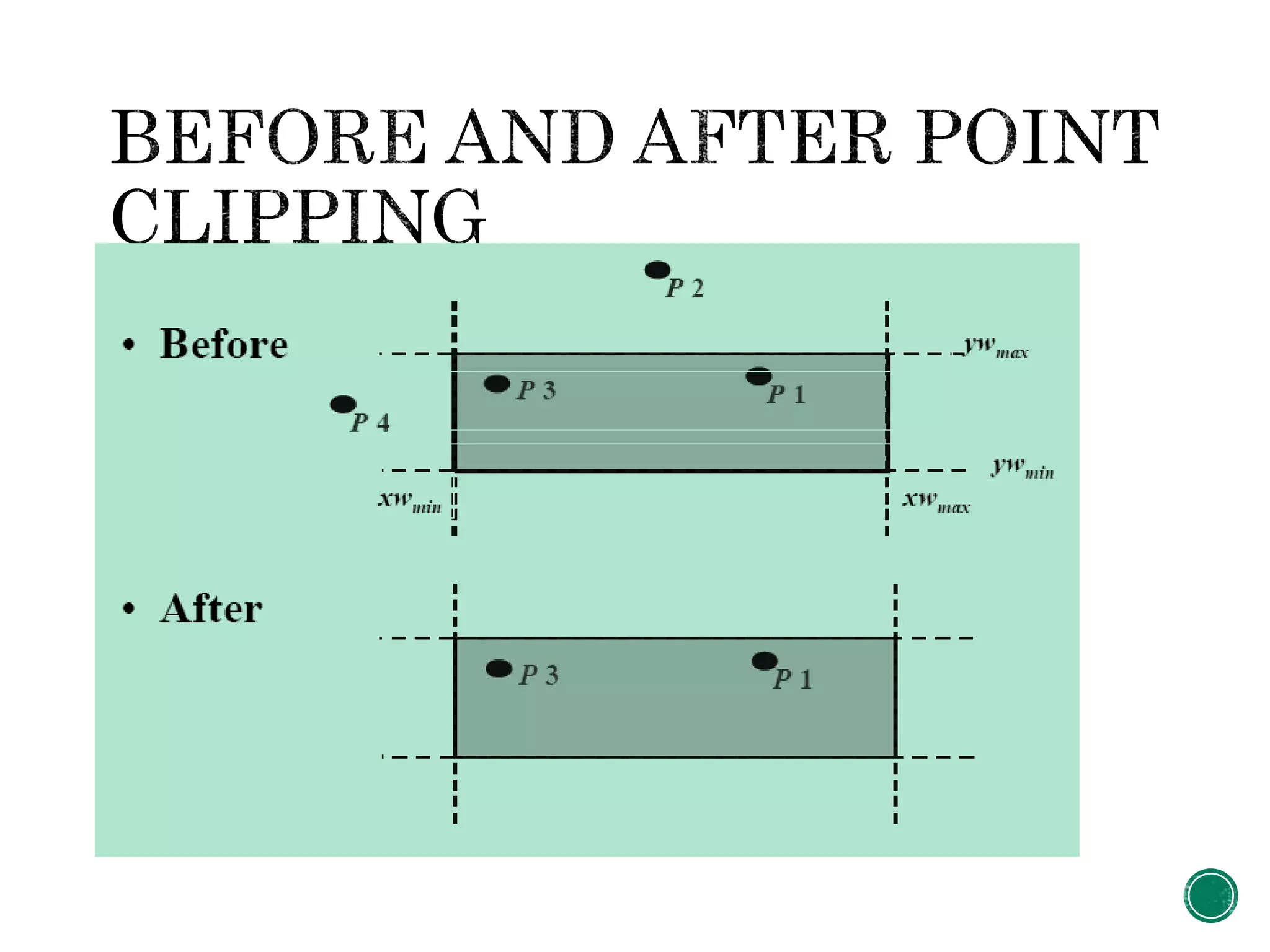
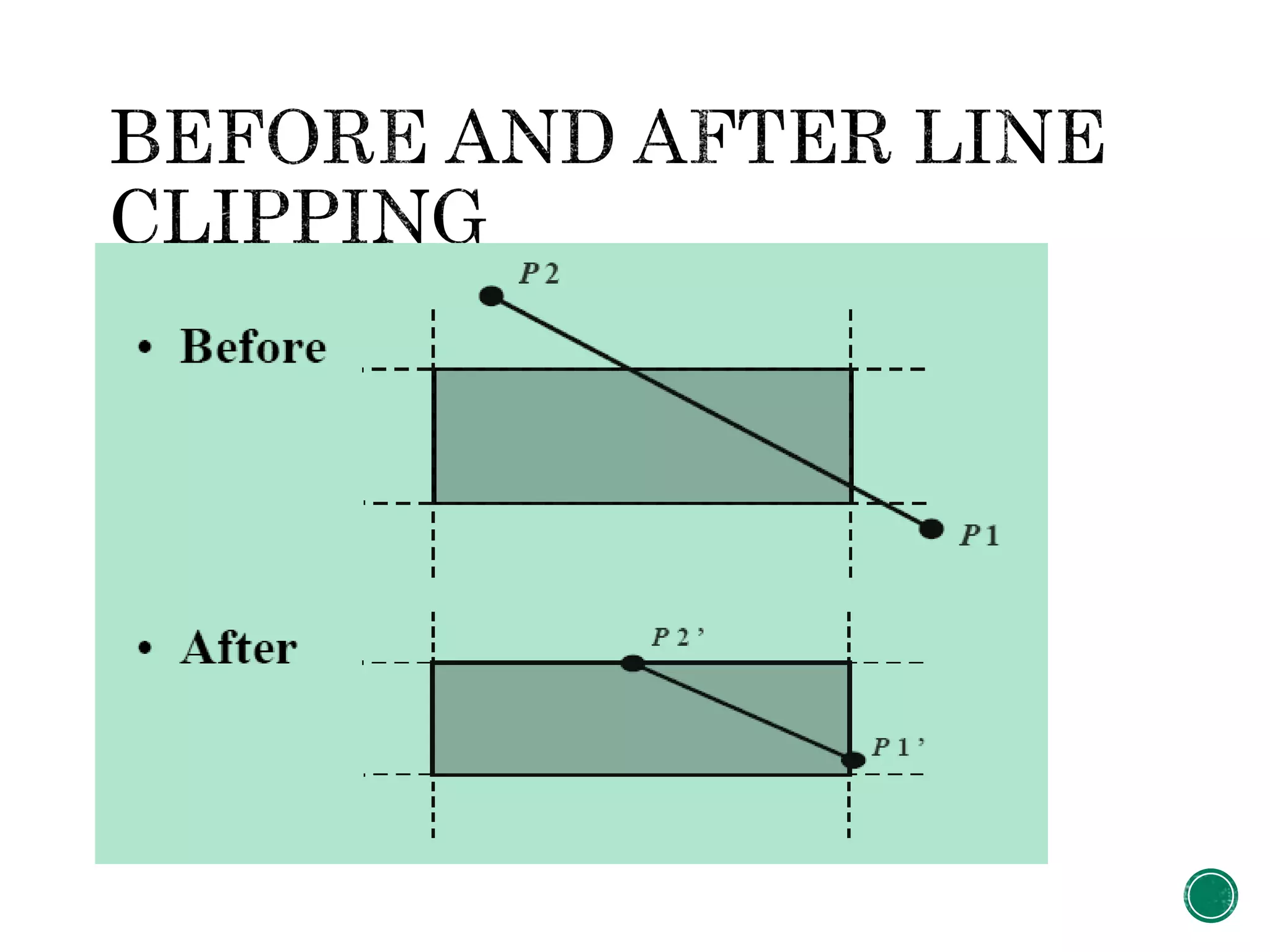
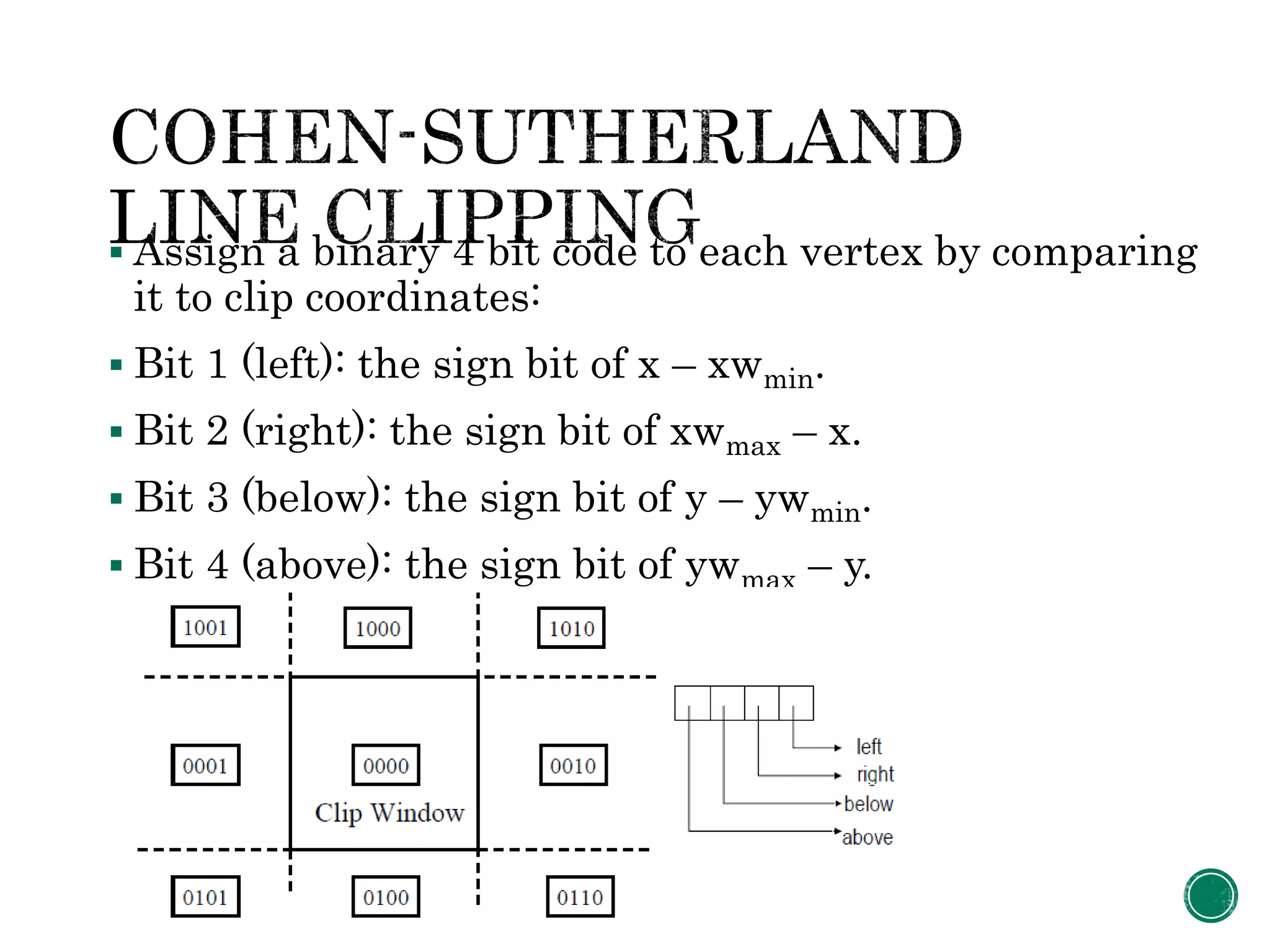
Clipping identifies portions of a scene outside a specified clip window region. There are different types of clipping for 2D graphics including all-or-none, point, line, and polygon clipping. The Cohen-Sutherland algorithm assigns a region code to line endpoints based on their position relative to the clip window boundaries, and uses logical AND operations on the codes to determine if a line is fully inside, outside, or needs clipping.

2.  Clipping means identifying portions of a scene that are
outside a specified region.
 For a 2D graphics the region defining what is to be
clipped is called the clip window.
 Types of clipping:
1. All-or-none clipping: If any part of object outside clip
window then the whole object is rejected.
2. Point clipping: Only keep the points that are inside clip
window.
3. Line clipping: Only keep segment of line inside clip
window.
4. Polygon clipping: Only keep segment of polygon inside
clip window.
5. Text clipping.

4.  Suppose that the clip window is a rectangle. The point
P = (x, y) is saved for display if the following are
satisfied:
xwmin ≤ x ≤ xwmax
ywmin ≤ y ≤ ywmax
 Otherwise, the point will be clipped (not saved for
display).

5.  P1= (10,20), P2= (30,50), P3= (60,90), and P4=
(130,150). Suppose that the coordinates of the two
opposite corners of the clip window are (xwmin, ywmin) =
(30, 30) and (xwmax, ywmax) = (130, 110). Which of the
above points will be clipped?
 P2 and P3 will saved because:
 For P2: 30 ≤ 30 ≤ 130 and 30 ≤ 50 ≤ 110.
 For P3: 30 ≤ 60 ≤ 130 and 30 ≤ 90 ≤ 110.

7.  For a line segment with endpoints (x1, y1) & (x2, y2)
and one or both endpoints outside the clipping
window, the parametric representation:
x= x1 + u(x2 – x1) and y= y1 + u(y2 – y1), where 0 ≤ u ≤ 1

8.  Line endpoints P1= (56,10) & P2= (62,16). Suppose that
the coordinates of the two opposite corners of the clip
window are (xwmin,ywmin)= (60,10) & (xwmax,ywmax)=
(70,16). Check the for clipping.
 x= 60= 56 + u(62 – 56), u= 4/6. So we deduce the line (56,10)-
(62,16) cross the left boundary (x = 60) of the clip window.
 x= 70= 56 + u(62 – 56), u= 14/6. So we deduce the line
(56,10)-(62,16) is not crossing the right boundary (x = 70) of
the clip window.
 y= 16= 10 + u(16 – 10), u= 6/6. So we deduce the line (56,10)-
(62,16) cross the top boundary (y = 16) of the clip window.
 y= 10= 10 + u(16 – 10), u= 0/6. So we deduce the line (56,10)-
(62,16) cross the bottom boundary (y = 10) of the clip
window.

9.  Step 1 − Assign a region code for each endpoints.
 Step 2 − If both endpoints have a region code 0000 then
accept this line.
 Step 3 − Else, perform the logical AND operation for both
region codes.
 Step 3.1 − If the result is not 0000, then reject the line.
 Step 3.2 − Else you need clipping.
 Step 3.2.1 − Choose an endpoint of the line that is outside
the window.
 Step 3.2.2 − Find the intersection point at the window
boundary.
 Step 3.2.3 − Replace endpoint with the intersection point
and update the region code.
 Step 3.2.4 − Repeat step 2 until we find a clipped line
either trivially accepted or trivially rejected.
 Step 4 − Repeat step 1 for other lines.

10.  Compute the end point Outcodes of A and B;
 if (A == 0000 && B == 0000)
 the whole line is visible (accept it);
 Else if (A AND B != 0000)
 the whole line is outside of window (reject it);
 else repeat the following {
 compute intersection;
 clip outside part;
 test again;}

11.  Assign a binary 4 bit code to each vertex by comparing
it to clip coordinates:
 Bit 1 (left): the sign bit of x – xwmin.
 Bit 2 (right): the sign bit of xwmax – x.
 Bit 3 (below): the sign bit of y – ywmin.
 Bit 4 (above): the sign bit of ywmax – y.

12.  Suppose that the coordinates of opposite corners of the
clip window are (68,59) & (92,71). Use Cohen-
Sutherland clipping line algorithm to find region codes
of the line (72,65)-(90,68), and the line (74,93)-(85,100),
and the line (60,50)-(120, 93).
 Solution:
1. Calculate differences between endpoint coordinates
and clipping boundaries.
2. Use the resultant sign bit of each difference
calculation to set the corresponding value in the
region code.

13.  Line (72,65)-(90,68):
 the region code of (72,65) is 0000
 the region code of (90,68) is 0000
 The line (72-65)-(90,68) is
completely inside

14.  Line (74,93)-(85,100):
 the region code of (74,93) is 1000
 the region code of (85,100) is 1000
 Since 1000 AND 1000 = 1000 (Non Zero), so the line
(74,93) – (85,100) lie completely outside the clipping
region. So we clip it.

15.  Line (60,50)-(120,95):
 the region code of (60,50) is 1010
 the region code of (120,95) is 0101
 The line is saved because the final region code is 0000.

16.  Suppose that the coordinates of opposite corners of the
clip window are (4,2) & (12,8). Use Cohen-Sutherland
clipping line algorithm to check the two endpoints (6,10)
and (13,15).
 the region code of (6,10) is 0001
 the region code of (120,95) is 0101
 With AND operation the region code is 0001 (Clipped).