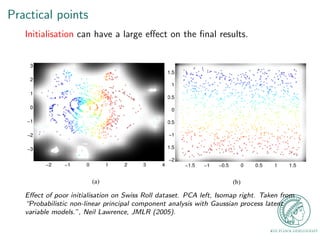
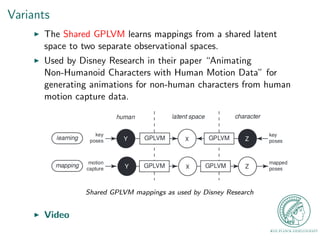
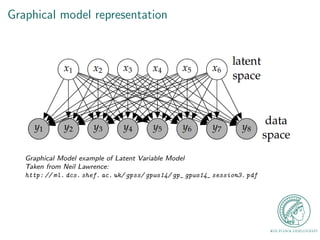
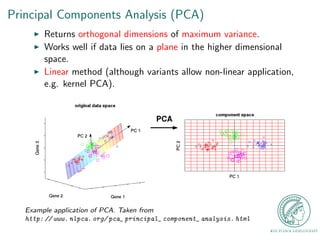
This document provides an outline for a talk on Gaussian Process Latent Variable Models (GPLVM). It begins with an introduction to why latent variable models are useful for dimensionality reduction. It then defines latent variable models and shows their graphical model representation. The document reviews PCA and introduces probabilistic versions like Probabilistic PCA (PPCA) and Dual PPCA. It describes how GPLVM generalizes these approaches using Gaussian processes. Examples applying GPLVM to face and motion data are provided, along with practical tips and an overview of GPLVM variants.

1. Gaussian Process Latent Variable Model
(GPLVM)
James McMurray
PhD Student
Department of Empirical Inference
11/02/2014

2. Outline of talk
Introduction
Why are latent variable models useful?
De

3. nition of a latent variable model
Graphical Model representation
PCA recap
Principal Components Analysis (PCA)
Probabilistic PCA based methods
Probabilistic PCA (PPCA)
Dual PPCA
GPLVM
Examples
Practical points
Variants
Conclusion
Conclusion
References

4. Why are latent variable models useful?
I Data has structure.

5. Why are latent variable models useful?
I Observed high-dimensional data often lies on a
lower-dimensional manifold.
Example Swiss Roll" dataset

6. Why are latent variable models useful?
I The structure in the data means that we don't need such high
dimensionality to describe it.
I The lower dimensional space is often easier to work with.
I Allows for interpolation between observed data points.

7. De

8. nition of a latent variable model
I Assumptions:
I Assume that the observed variables actually result from a
smaller set of latent variables.
I Assume that the observed variables are independent given the
latent variables.
I Diers slightly from dimensionality reduction paradigm which
wishes to

9. nd a lower-dimensional embedding in the
high-dimensional space.
I With the latent variable model we specify the functional form
of the mapping:
y = g(x) +
where x are the latent variables, y are the observed variables
and is noise.
I Obtain dierent latent variable models for dierent
assumptions on g(x) and

10. Graphical model representation
Graphical Model example of Latent Variable Model
Taken from Neil Lawrence:
http: // ml. dcs. shef. ac. uk/ gpss/ gpws14/ gp_ gpws14_ session3. pdf

11. Plan
Introduction
Why are latent variable models useful?
De

12. nition of a latent variable model
Graphical Model representation
PCA recap
Principal Components Analysis (PCA)
Probabilistic PCA based methods
Probabilistic PCA (PPCA)
Dual PPCA
GPLVM
Examples
Practical points
Variants
Conclusion
Conclusion
References

13. Principal Components Analysis (PCA)
I Returns orthogonal dimensions of maximum variance.
I Works well if data lies on a plane in the higher dimensional
space.
I Linear method (although variants allow non-linear application,
e.g. kernel PCA).
Example application of PCA. Taken from
http: // www. nlpca. org/ pca_ principal_ component_ analysis. html

14. Plan
Introduction
Why are latent variable models useful?
De

15. nition of a latent variable model
Graphical Model representation
PCA recap
Principal Components Analysis (PCA)
Probabilistic PCA based methods
Probabilistic PCA (PPCA)
Dual PPCA
GPLVM
Examples
Practical points
Variants
Conclusion
Conclusion
References

16. Probabilistic PCA (PPCA)
I A probabilistic version of PCA.
I Probabilistic formulation is useful for many reasons:
I Allows comparison with other techniques via likelihood
measure.
I Facilitates statistical testing.
I Allows application of Bayesian methods.
I Provides a principled way of handling missing values - via
Expectation Maximization.

17. PPCA De

18. nition
I Consider a set of centered data of n observations and d
dimensions: Y = [y1; : : : ; yn]T .
I We assume this data has a linear relationship with some
embedded latent space data xn. Where Y 2 RND and
x 2 RNq.
I yn = Wxn + n, where xn is the q-dimensional latent variable
associated with each observation, and W 2 RDq is the
transformation matrix relating the observed and latent space.
I We assume a spherical Gaussian distribution for the noise with
a mean of zero and a covariance of

19. 1I
I Likelihood for an observation yn is:
p (ynjxn;W;

20. ) = N
ynjWxn;

21. 1I

22. PPCA Derivation
I Marginalise latent variables xn, put a Gaussian prior on W and
solve using maximum likelihood.
I The prior used for xn in the integration is a zero mean, unit
covariance Gaussian distribution:
p(xn) = N(xnj0; I)
p(ynjW;

23. ) =
Z
p(ynjxn;W;

24. )p(xn)dxn
p(ynjW;

25. ) =
Z
N
ynjWxn;

26. 1I
N(xnj0; I)dxn
p(ynjW;

27. ) = N(ynj0;WWT +

28. 1I)
I Assuming i.i.d. data, the likelihood of the full set is the
product of the individual probabilities:
p(Y jW;

29. ) =
YN
n=1
p(ynjW;

30. )

31. PPCA Derivation
I To calculate that marginalisation step we use the summation
and scaling properties of Gaussians.
I Sum of Gaussian variables is Gaussian.
Xn
i=1
N(i ; 2
i ) N
Xn
i=1
i ;
Xn
i=1
2
i
!
I Scaling a Gaussian leads to a Gaussian:
wN(; 2) N(w;w22)
I So:
y = Wx + ; x N(0; I) ; N(0; 2I)
Wx N(0;WWT)
Wx + N(0;WWT + 2I)