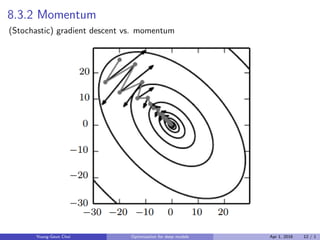
Chapter 8 of Goodfellow et al. (2016) discusses optimization techniques for training deep models, highlighting the distinctions between learning and pure optimization, and detailing various algorithms like stochastic gradient descent (SGD), momentum, and adaptive methods such as Adam. It tackles challenges such as ill-conditioning, local minima, and issues specific to neural networks, like the vanishing and exploding gradient problems. The chapter also outlines strategies for parameter initialization and the importance of batch normalization in improving the training process.

1. Chap 8. Optimization for training deep models
(Goodfellow et al. (2016), Deep Learning, MIT Press)
Presenter : Young-Geun Choi
Department of Statistics
Seoul National University
Apr 1, 2016
Young-Geun Choi Optimization for deep models Apr 1, 2016 1 / 1

2. Young-Geun Choi Optimization for deep models Apr 1, 2016 2 / 1

3. 8.1 How learning differs from pure optimization
Cost function is estimated by empirical risk – (1) indirectly evaluated and
(2) separable.
(1) Cost function:
J(θ) = E(x,y)∼ˆpdata
L(f(x; θ), y).
(try to) estimate true
J∗
(θ) = E(x,y)∼pdata
L(f(x; θ), y)
(2) N : size of all training example
E(x,y)∼ˆpdata
L(f(x; θ), y) =
1
N
N∑
i=1
L(f(x(i)
; θ), y(i)
).
Young-Geun Choi Optimization for deep models Apr 1, 2016 3 / 1

4. 8.1.3 Batch and minibatch algorithms
We may use gradient descent : θnew
= θold
− ϵ ▽θ J∗
(θold
) for optimization.
Is using all samples good to estimate J∗
(θ) or ▽θJ∗
(θ)?
Standard error of mean is approximated by σ/
√
N (CLT)
10,000 times more examples give 100 times more accuracy
There also might be redundancy in the training set (many samples might be
very similar)
→ Use subsets (minibatch) of size m to estimate ▽θJ∗
(θ)
Caution (confusing terminologies)
Batch or deterministic gradient methods : processing with all training
examples
e.g. “Batch gradient descent” : use full training set
e.g. “minibatch (stochastic) gradient descent” : stochastic gradient descent
(Sec 8.3-)
Batch size : the size of a minibatch
Young-Geun Choi Optimization for deep models Apr 1, 2016 4 / 1

5. 8.1.3 Batch and minibatch algorithms
Batch sizes (minibatch sizes) are generally driven by
Minimum batch size : below which there is no reduction in the time to
process a minibatch due to multicore architecture
Typically all examples in a (mini)batch are to be processed in parallel;
amount of memory scales matters
When using GPU, m = 2p
will be good (32, 256, 4096)
Very large dataset – rather than randomly select examples, shuffle and stack
in advance and consecutively select them
Young-Geun Choi Optimization for deep models Apr 1, 2016 5 / 1

6. 8.2 Challenges in neural network optimization
Deep neural network cost function
Many composition of functions
Many parameters
Non-identifiability
8.2.1 Ill-conditioning
Hessian matrix can be ill-conditioned (very large maximum eigenvalue, very
small minimum eigenvalue)
Very small step can increase the cost function
8.2.2 Local minima
Any deep models essentially have an extremely large number of local minima
due to weight space symmetry.
Experts suspect that most local minima have a low cost function value – it is
not important to find the global minima
Young-Geun Choi Optimization for deep models Apr 1, 2016 6 / 1

7. 8.2 Challenges in neural network optimization
8.2.3 Plateaus, saddle points and other flat regions
Zero-gradient points are more likely to be saddle points in higher dimension
(more parameters).
Can optimization algorithms (introduced later) escape saddle points? – check
https://github.com/cs231n/cs231n.github.io/blob/master/
neural-networks-3.md#sgd
Flat regions (zero Hessian, zero gradient) even matter
8.2.4 Cliffs, exploding gradients
Highly deep neural network, or recurrent neural networks often contains sharp
nonlinearities.
Very high derivative at some place can catapult the parameters very far,
possibly spoiling most the optimization work that had been done.
Young-Geun Choi Optimization for deep models Apr 1, 2016 7 / 1

8. 8.2 Challenges in neural network optimization
8.2.5 Long-term dependencies
In recurrent neural networks (Chap 10), repeatedly a matrix is multiplied;
vanishing and exploding gradient problem can occur
8.2.6 Inexact gradients
We use samples – can lead to a noisy or even biased estimate
8.2.7 Poor correspondence between local and global structure
Can we make a non-local move? Rather, find good initial points.
Young-Geun Choi Optimization for deep models Apr 1, 2016 8 / 1

9. 8.2 Challenges in neural network optimization
8.2.8 Theoretical limits of optimization
Some theory: output discrete (but practical NN units output smoothly
increasing values and local search is feasible)
Some theory: problem classes that are intractable (but it is difficult to tell a
problem is in the class)
Some theory: a network of a given size is intractable (but a larger network
can find a solution)
Developing more realistic bounds on the performance of optimization
algorithms therefore remains an important goal for machine learning research.
Young-Geun Choi Optimization for deep models Apr 1, 2016 9 / 1

10. 8.3 Basic algorithms: 8.3.1 Stochastic gradient descent
(SGD)
Algorithm SGD update at training iteration k
Require: Learning rate ϵ = ϵk
Require: Initial parameter θ
1: while stopping criterion not met do
2: Sample a minibatch {x(1)
, . . . , x(m)
} and corresponding y(i)
3: Compute gradient descent estimate: g ← 1
m ▽θ
∑
i L(f(x(i)
; θ), y(i)
))
4: Apply update: θ ← θ − ϵg
5: end while
Learning rate, initial point are kind of hyper-parameters.
Learning rate ϵk depends on iteration index k
SGD convergence: when
∑∞
k=1 ϵk = ∞ and
∑∞
k=1 ϵ2
k < ∞
In practice, decay linearly until iteration τ:
ϵk =
(
1 −
k
τ
)
ϵ0 +
k
τ
ϵτ
After iteration τ, leave ϵk constant. Usually ϵτ is 1% of ϵ0.
Young-Geun Choi Optimization for deep models Apr 1, 2016 10 / 1

11. 8.3.1 Stochastic gradient descent (SGD)
τ may be set to the number of iterations required to make a few hundred
passes through the training set.
How to set ϵ0? Monitor learning curves.
Check plots in https://github.com/cs231n/cs231n.github.io/blob/
master/neural-networks-3.md#sgd
Optimal ϵ0 (in terms of total training time and the final cost value) is higher
than the learning rate that yields the best performance after 100 iterations
and so.
SGD computation time (per update) does not grow with the number of
training examples.
Excess error (J(θ) − minθ J(θ)) of SGD after k iterations
▶ O(1/
√
k) for convex
▶ O(1/k) for strong convex
▶ Cramer-Rao bound : generalization error cannot decrease faster than O(1/k)
▶ Algorithms introduced later are good in practice, but lost in the constant
factors hidden in O(1/k).
Young-Geun Choi Optimization for deep models Apr 1, 2016 11 / 1

12. 8.3.2 Momentum
(Stochastic) gradient descent vs. momentum
Young-Geun Choi Optimization for deep models Apr 1, 2016 12 / 1

13. 8.3.2 Momentum
Algorithm SGD with momentum
Require: Learning rate ϵ = ϵk, momentum parameter α
Require: Initial parameter θ, initial velocity v
1: while stopping criterion not met do
2: Sample a minibatch {x(1)
, . . . , x(m)
} and corresponding y(i)
3: Compute gradient descent estimate: ˆg ← 1
m ▽θ
∑
i L(f(x(i)
; θ), y(i)
))
4: Compute velocity update: v ← αv − ϵg
5: Apply update: θ ← θ + v
6: end while
Speed decreasing from v to αv is an analogy from ‘viscous drag’.
Young-Geun Choi Optimization for deep models Apr 1, 2016 13 / 1

14. 8.3.3 Nesterov Momentum
Algorithm SGD with Nesterov momentum
Require: Learning rate ϵ = ϵk, momentum parameter α
Require: Initial parameter θ, initial velocity v
1: while stopping criterion not met do
2: Sample a minibatch {x(1)
, . . . , x(m)
} and corresponding y(i)
3: Compute gradient descent estimate: ˆg ← 1
m ▽θ
∑
i L(f(x(i)
; θ+αv), y(i)
))
4: Compute velocity update: v ← αv − ϵg
5: Apply update: θ ← θ + v
6: end while
Excess error is O(1/k2
) for convex batch gradient
In SGD, it does not improve rate of convergence.
Young-Geun Choi Optimization for deep models Apr 1, 2016 14 / 1

15. 8.4 Parameter initialization strategies
Nonconvex cost function: initial point strongly affects training.
No rule of thumb.
Some helpful comments (Weights)
Break symmetry – no same wij
Consider Gaussian or uniform U
(
− 1√
J
, 1√
J
)
(J : input layer size).
Large initial value may lead to overfitting.
Bias : okay to set zero
Young-Geun Choi Optimization for deep models Apr 1, 2016 15 / 1

16. 8.5 Algorithms with adaptive learning rates: 8.5.1 AdaGrad
Learning rate : the most difficult to set, high impact on model performance
Can we determine it in adaptive way?
Algorithm The AdaGrad algorithm
Require: Global learning rate ϵ
Require: Initial parameter θ
Require: Small constant δ, perhaps 10−7
for numerical stability
1: Initialize gradient accumulation variable r = 0
2: while stopping criterion not met do
3: Sample a minibatch {x(1)
, . . . , x(m)
} and corresponding y(i)
4: Compute gradient descent estimate: g ← 1
m ▽θ
∑
i L(f(x(i)
; θ), y(i)
))
5: Accumulated squared descent : r ← r + g ⊙ g
6: Compute update: ∆θ ← − ϵ
δ+
√
r
⊙ g (operations elementwise)
7: Apply update: θ ← θ + ∆θ
8: end while
Accumulation of squared gradients from the beginning of training can result
in a premature and excessive decrease in effect learning rate.
Young-Geun Choi Optimization for deep models Apr 1, 2016 16 / 1

17. 8.5.2 RMSProp
Algorithm The RMSProp algorithm
Require: Global learning rate ϵ, decay rate ρ
Require: Initial parameter θ
Require: Small constant δ, usually 10−6
for numerical stability
1: Initialize gradient accumulation variable r = 0
2: while stopping criterion not met do
3: Sample a minibatch {x(1)
, . . . , x(m)
} and corresponding y(i)
4: Compute gradient descent estimate: g ← 1
m ▽θ
∑
i L(f(x(i)
; θ), y(i)
))
5: Accumulated squared descent : r ← ρr + (1 − ρ)g ⊙ g
6: Compute update: ∆θ ← − ϵ
δ+
√
r
⊙ g (operations elementwise)
7: Apply update: θ ← θ + ∆θ
8: end while
Learning trajectory may pass through many different structures and
eventually arrive at a region that is not a locally convex bowl.
Practically good.
Young-Geun Choi Optimization for deep models Apr 1, 2016 17 / 1

18. 8.5.2 RMSProp
Algorithm The RMSProp algorithm with Nesterov momentum
Require: Global learning rate ϵ, decay rate ρ
Require: Initial parameter θ, initial velocity v
1: Initialize gradient accumulation variable r = 0
2: while stopping criterion not met do
3: Sample a minibatch {x(1)
, . . . , x(m)
} and corresponding y(i)
4: Compute gradient descent estimate: g ← 1
m ▽θ
∑
i L(f(x(i)
; θ+αv), y(i)
))
5: Accumulated squared descent : r ← ρr + (1 − ρ)g ⊙ g
6: Compute velocity update: v ← αv − − ϵ√
r
⊙ g (operations elementwise)
7: Apply update: θ ← θ + v
8: end while
Young-Geun Choi Optimization for deep models Apr 1, 2016 18 / 1

19. 8.5.3 Adam
Algorithm The Adam algorithm
Require: Global learning rate (step size) ϵ
Require: Exponential decay rates for moment estimates, ρ1 and ρ2 in [0, 1) (Suggested defaults:
0.9 and 0.999, resp.
Require: Small constant δ for numerical stabilization (Suggested 10−8)
Require: Initial parameter θ
1: Initialize 1st and 2nd moment variables s = 0, r = 0
2: Initialize timestep t = 0
3: while stopping criterion not met do
4: Sample a minibatch {x(1), . . . , x(m)} and corresponding y(i)
5: Compute gradient descent estimate: g ← 1
m
▽θ
∑
i L(f(x(i); θ), y(i)))
6: t ← t + 1
7: Update biased first moment update: s ← ρ1s + (1 − ρ1)g
8: Update biased second moment update: r ← ρ2r + (1 − ρ2)g ⊙ g
9: Correct bias in first moment: ˆs ← s
1−ρt
1
10: Correct bias in second moment: ˆr ← r
1−ρt
2
11: Compute update: ∆θ = −ϵ ˆs√
ˆr+δ
(operations elementwise)
12: Apply update: θ ← θ + ∆θ
13: end while
Momentum + RMSProp + Some more insights
Fairly robust to hyperparameter choice, learning rate sometimes needs change
Young-Geun Choi Optimization for deep models Apr 1, 2016 19 / 1

20. 8.5.4 Choosing the right optimization algorithm
Currently popular are SGD (with/out momentum), RMSProp (with/out
momentum), AdaDelta, and Adam
Choice (at this point) seems to depend largely on the user’s familiarity with
the algorithm (for ease of hyperparameter tuning)
8.6 Approximate second-order methods – Omitted here (practically not used)
Newton’s method
Conjugate gradients
BFGS
Young-Geun Choi Optimization for deep models Apr 1, 2016 20 / 1

21. 8.7 Optimization strategies and meta-algorithms: 8.7.1
Batch normalization
Notation change : j-th unit in l-th layer revisited
h
(l)
j = ϕ


J(l−1)
∑
k=1
w
(l)
k,jh
(l−1)
k + b
(l)
j

 , j = 1, . . . , J(l)
Vector notation
h(l)
= ϕ
(
W(l)
h(l−1)
+ b(l)
)
Motivation
Each layer is affected by preceding layers. Then for deeper networks,
▶ Small changes to the network parameters amplify.
▶ Simultaneous update of all layers even matters.
▶ Gradient vanishing ϕ′
(t) even for ReLU function and good initial point
Empirically, training converges faster if input (h(l−1)
) distribution is fixed.
▶ If we have l = F2(F1(u, θ1), θ2), learning θ2 can be viewed by (x = F1(u, θ1))
l = F2(x, θ2), θnew
2 = θold
2 −
α
m
m∑
i=1
∂F2(xi, θold
2 )
∂θ2
▶ But simply normalizing each input (of a layer) may change the layer can
represent.
Young-Geun Choi Optimization for deep models Apr 1, 2016 21 / 1

22. 8.7.1 Batch normalization
h(l)
= ϕ
(
W(l)
h(l−1)
+ b(l)
)
rewrite
−→ ϕ (Wx + b) .
Let’s say we have inputs {x1, . . . , xm} (xi : activations of the previous layer for
i-th example).
Algorithm Batch normalizing transform – When learn W and b, learn γ, β too.
Require: B = {x1, . . . , xm}, parameter to be learned: γ, β
Ensure: yi = BNγ,β(xi)
1: Mini-batch mean: µB ← 1
m
∑m
i=1 xi
2: Mini-batch variance: σ2
B ← 1
m
∑m
i=1(xi − µB)2
3: Normalize: ˆxi ← xi−µB√
σ2
B+ϵ
4: Scale and shift: yi ← γˆxi + β ≡ BNγ,β(xi)
Young-Geun Choi Optimization for deep models Apr 1, 2016 22 / 1

23. 8.7.1 Batch normalization
ϕ (Wxi + b)
ˆxi ←
xi − µB
√
σ2
B + ϵ
, yi ← γˆxi + β ≡ BNγ,β(xi)
x’s have heterogeneous mean and variance over minibatches which heavily
depends on previous layers
On the other hand, y’s have same mean and variance over minibatches which
determined sole by γ, β which is much easier to learn with gradient descent.
In practice, batch-normalize the whole Wx + b rather than x itself (b then
should be omitted)
14 times fewer training steps, first place in ImageNet (2014)
Young-Geun Choi Optimization for deep models Apr 1, 2016 23 / 1

24. 8.7 Optimization strategies and meta-algorithms
8.7.2 Coordinate descent
Optimize coordinate-wisely
Used to be good for convex problems
8.7.3 Polyak averaging
(Moving) average over gradient descent visit points
8.7.4 Supervised pretraining
Young-Geun Choi Optimization for deep models Apr 1, 2016 24 / 1

25. 8.7 Optimization strategies and meta-algorithms
8.7.5 Designing models to aid optimization
In practice, it is more important to choose a model family that is easy to
optimize than to use a powerful optimization algorithm.
LSTM, ReLU, maxout units have all moved toward easier optimization.
8.7.6 Continuation methods and curriculum learning
Young-Geun Choi Optimization for deep models Apr 1, 2016 25 / 1