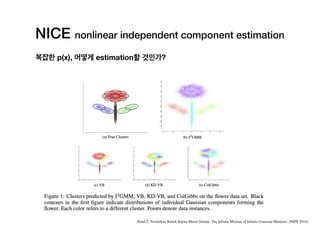
NICE: Non-linear Independent Components Estimation
Laurent Dinh, David Krueger, Yoshua Bengio. 2014.
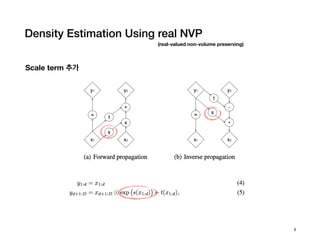
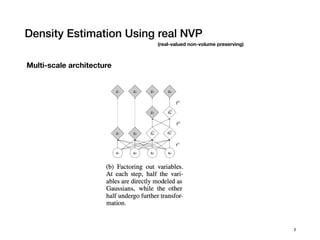
Density estimation using Real NVP
Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio. 2017.
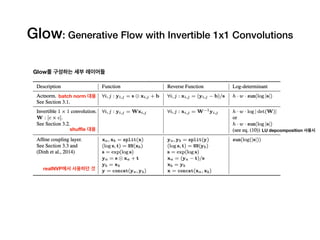
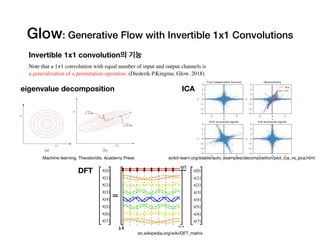
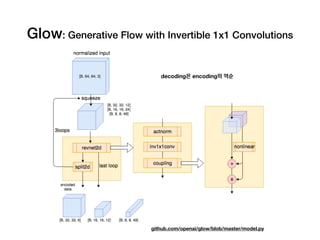
Glow: Generative Flow with Invertible 1x1 Convolutions
Diederik P. Kingma, Prafulla Dhariwal. 2018.
논문 리뷰 자료