東京大学松尾研究室におけるPRML輪読資料です。

1. PRML輪読会 2017
第14章 モデルの結合
東京⼤学⼤学院⼯学系研究科
技術経営戦略学専攻
松尾研究室
⼤野 峻典

2. 構成
14.1 ベイズモデル平均化
14.2 コミッティ
14.3 ブースティング
14.4 ⽊構造モデル
14.5 条件付き混合モデル
2

3. モデルの結合
• 複数のモデルを何らかの⽅法で組み合わせることで、単⼀のモデルを独⽴に
利⽤するよりも性能改善できること多い.
– コミッティ：複数の異なるモデルの予測の平均値を予測値として⽤いるような⽅法はコ
ミッティと呼ばれる. (→ 14.2)
• ブースティング：複数のモデルを逐次的に訓練する⼿法. コミッティ技術の1つ. (→14.3)
– 予測に⽤いるモデルを⼊⼒変数の関数として選択する.
• 異なる領域の予測をそれぞれのモデルが担当.
• 決定⽊（→14.4）：⼊⼒空間をハードに分割
– 混合エキスパートモデル （→14.5）
• 確率的な枠組みの導⼊により、決定過程をソフトにする.
3

4. 14.1 ベイズモデル平均化
• ベイズモデル平均化と、モデルの結合は違う、ということを理解する。
• ベイズモデル平均化： 例
– p(h)：あるモデルが選択される確率
– p(X|h)：あるモデルを選んだ時のデータ集合全体の⽣成確率
– Σでhに関して和の解釈： 本来は1つのモデルがデータ集合全体の⽣成を担当しており、
hの確率分布は単純にいずれのモデルであるかの不確実性を反映するという解釈
– → データ集合のサイズが⼤きくなればこの不確実性は減少し、事後確率p(h|X)は漸近
的に1つのモデルに収束する。
• モデルの結合
– 観測されたデータ点x毎に対応する潜在変数zが存在する
– 潜在変数zはデータ点の⽣成原因がどのモデルなのか⽰す
• Ex) 混合ガウス分布
4

5. 14.2 コミッティ
• モデル集合内からの個々の予測を平均化する。
• モデル誤差（3.2節）
– バイアス：モデルと真の予測すべき関数との差異
– バリアンス：モデルの個々のデータ点に対する感度
• バリアンスが⼤きくても、平均化することで予測性能は改善される
5

6. 14.2 コミッティ
• 平均を取るといってもデータ集合は1つしかないので、異なるモデル間に変
化を導⼊する⽅法が必要である.
– → M個のブートストラップ集合を作る.
• ブートストラップとは（1.2.3節）
– データセットから復元抽出でN個のデータを取り出したものを、Mセット作る⼿法. (M
個のブートストラップ集合)
• ブートストラップ集約（バギング）
– ym(x)：各ブートストラップ集合で訓練したM個の予測モデル
– コミッティの予測
6

7. 14.2 コミッティ
• 誤差が⼩さくなる理由を数式で⽰す。
• 本当の回帰係数h(x)で, 各モデルの出⼒が本当の値に誤差を加算した式とす
ると,
• 平均⼆乗誤差：
• モデルの誤差の平均値：
• モデルの結合による誤差：
• 誤差の平均が0で無相関であると過程すると
– M個の異なるモデルを平均することで、モデルの平均誤差を1/Mに低減できるという.
– 実際には, 各モデルの誤差が無相関であるという仮説は成り⽴たないので, ここまでは
低減できない. (が、誤差は⼩さくなる.)
7

8. 14.3 ブースティング
• コミッティを使う⼿法の別の例.
• ブースティング
– 複数のベース分類器（弱学習器）を結合するモデル
• ベース分類器がランダムな判定より少し優れただけであっても、良い結果を出せ性能⾼い！
– 分類のために設計されたものだが、回帰にも拡張可能.
8

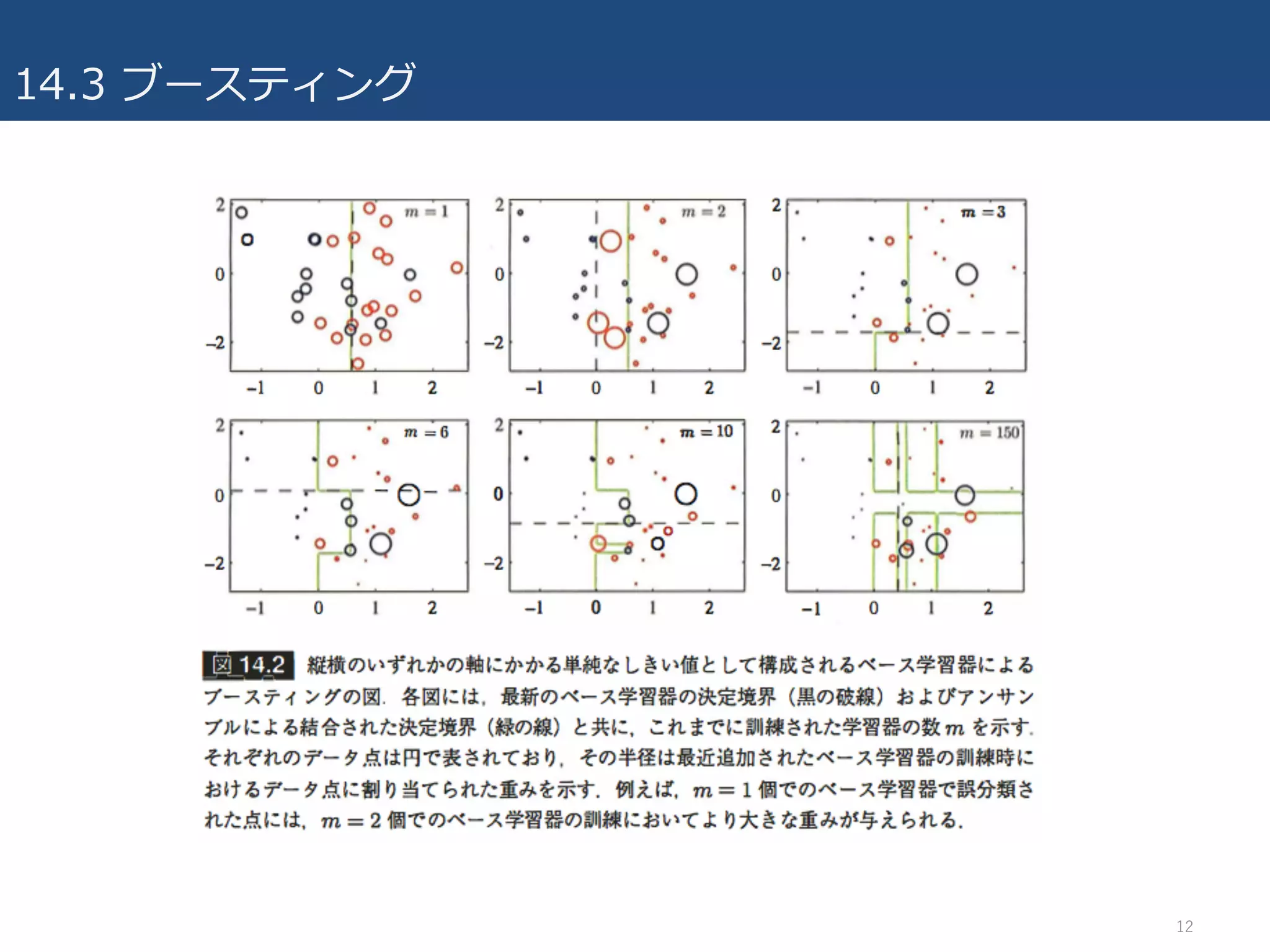
9. 14.3 ブースティング
• AdaBoost：最も広く利⽤されているブースティングアルゴリズム
– Adaptive Boosting
– ベース分類器を重み付訓練データによって逐次的に訓練
• 直前のベース学習器の分類結果に基いて次の重みを計算（その時点までのベース分類器で誤
分類されたデータ点により⼤きな重みを与える.）
• 例：ニクラス分類問題
– 初期重みは1/N
– 誤分類されたデータ点の重みは増加
» 直前で苦⼿だった事例を分類できるように
– 最終的にベース分類器毎に算出した重み係数を⽤いて
結合
– バギングとの違い：バギングでは独⽴した訓練データからモデルを学習
9

10. 14.3 ブースティング
• AdaBoostの正確な定式化（t={0,1}のニクラス分類想定）
10

11. 14.3 ブースティング
• AdaBoost意味解説
– 最初のベース分類器y1(x)では全てが等しい重み係数wn
(1)を⽤いて訓練するので、単⼀
の分類器を訓練する通常の⼿続きと同じ.
– (14.18)のように、続く反復計算では、誤分類したデータ点に対しては重み係数を変え
ない. → 逐次的に訓練される分類器では、それ以前の分類器誤分類されたデータ点が強
調される。
– 値εmは各ベース分類器の重み付けされたデータ集合に対する誤差率の尺度である。
• → 最終的に全体としての出⼒を計算する(14.19)では, (14.17)で定義する重み係数αmを⽤い
て、より正確な分類器に対する重みを⼤きくしている.
11

12. 14.3 ブースティング
12

13. 14.3.1 指数誤差の最⼩化
• 指数関数の逐次的最⼩化を考えると、ブースティングを単純に解釈できる
– 指数誤差関数 E
• fm(x)はベース分類器yl(x)の線形結合
• ⽬標値tn∈{-1,1}
– ⽬的：重み係数αlとベース学習器yl(x)のパラメータ両⽅についてEを最⼩化すること.
– ベース分類器y1(x)…ym-1(x)とそれらの係数α1…αm-1が固定されているとし、αmと
ym(x)に関してのみ最⼩化⾏う. ym(x)の寄与を分離し、誤差関数を以下のように変形.
• ここでαmとym(x)のみ最⼩化するので、係数wn
(m)=exp{-tnfm-1(xn)}は定数とみなせる.
13

14. 14.3.1 指数誤差の最⼩化
– ym(x)で正しく分類されるデータ点の集合をTmとし, 誤分類される点をMmとすると, 以
下のように誤差関数かける
– 第⼆項は定数であり、和の前の全体に対する定数係数は極⼩値計算に影響与えないので、
この14.23の最⼩化は、14.15を最⼩化するのと等価. 同様にαmに関する最⼩化を⾏う
と14.17が得られる.
• 14.22に基づき, 得られたαmとym(x)を含む以下の式でデータ点の重み更新
– 計算すると（省略. p379参照.）14.18得る.
• 最終的に, 全てのベース分類器の訓練終わると, 新しいデータ点は14.21で
定義される関数の符号を評価し分類できる. 14.19を得る.
• 式変形に関して詳しかった資料
14

15. 14.3.2 ブースティングのための誤差関数
• AdaBoostアルゴリズムで最⼩化される指数誤差関数は、これまで（13章ま
で）で⾒てきた指数関数とは異なる.
• この節では、指数誤差関数の性質について考える.
• AdaBoostで⽤いられる指数誤差の期待損失：
• 全ての可能な関数y(x)についての変分最⼩化を実⾏すると、次式得られる
（⇛演習14.7）
– 対数オッズの半分の値
– → AdaBoostは逐次的な最適化戦略という制約のもと、最良の対数オッズ⽐の近似を、
ベース学習器の線形結合による空間内で探索する.
15

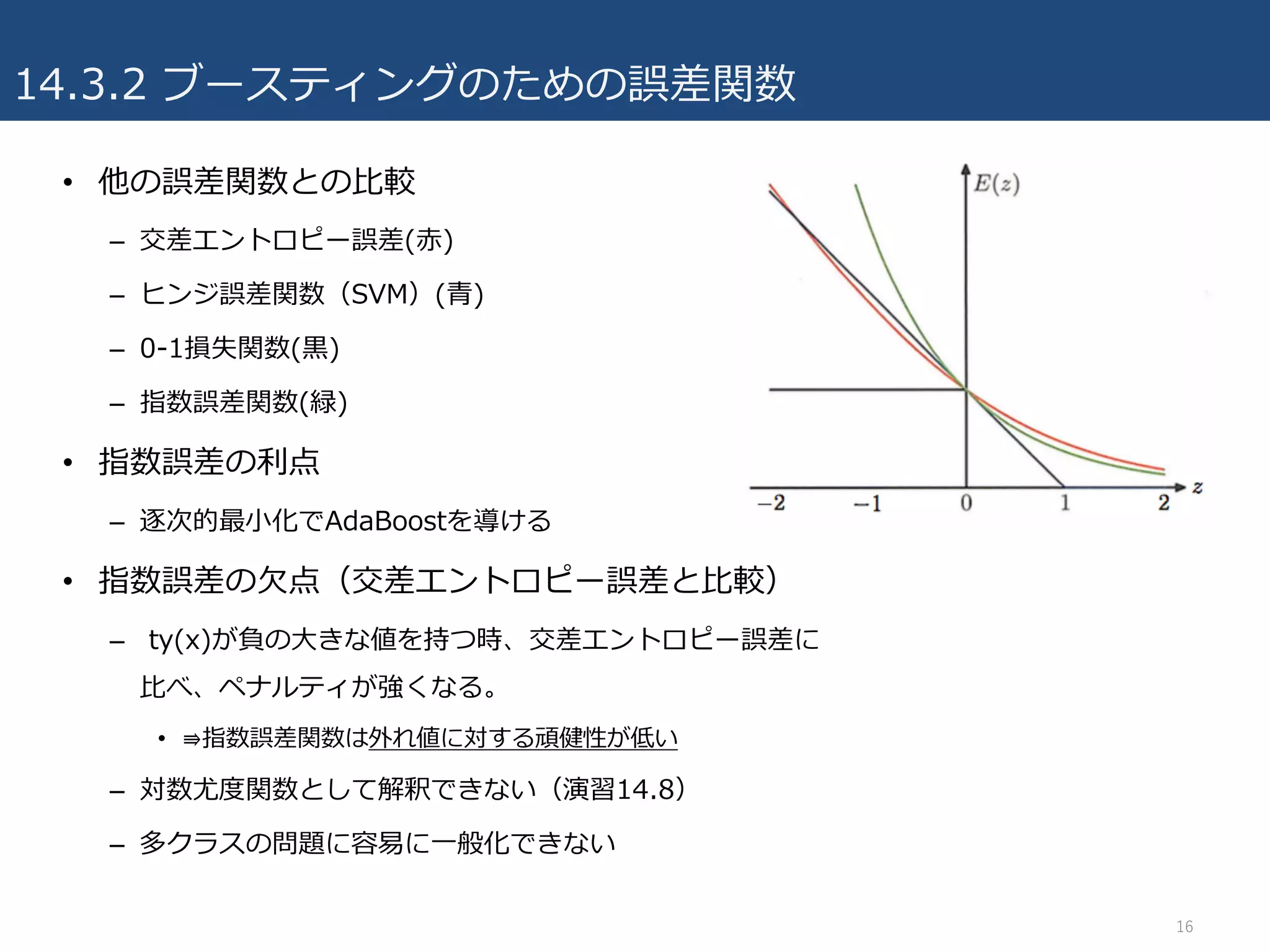
16. 14.3.2 ブースティングのための誤差関数
• 他の誤差関数との⽐較
– 交差エントロピー誤差(⾚)
– ヒンジ誤差関数（SVM）(⻘)
– 0-1損失関数(⿊)
– 指数誤差関数(緑)
• 指数誤差の利点
– 逐次的最⼩化でAdaBoostを導ける
• 指数誤差の⽋点（交差エントロピー誤差と⽐較）
– ty(x)が負の⼤きな値を持つ時、交差エントロピー誤差に
⽐べ、ペナルティが強くなる。
• ⇛指数誤差関数は外れ値に対する頑健性が低い
– 対数尤度関数として解釈できない（演習14.8）
– 多クラスの問題に容易に⼀般化できない
16

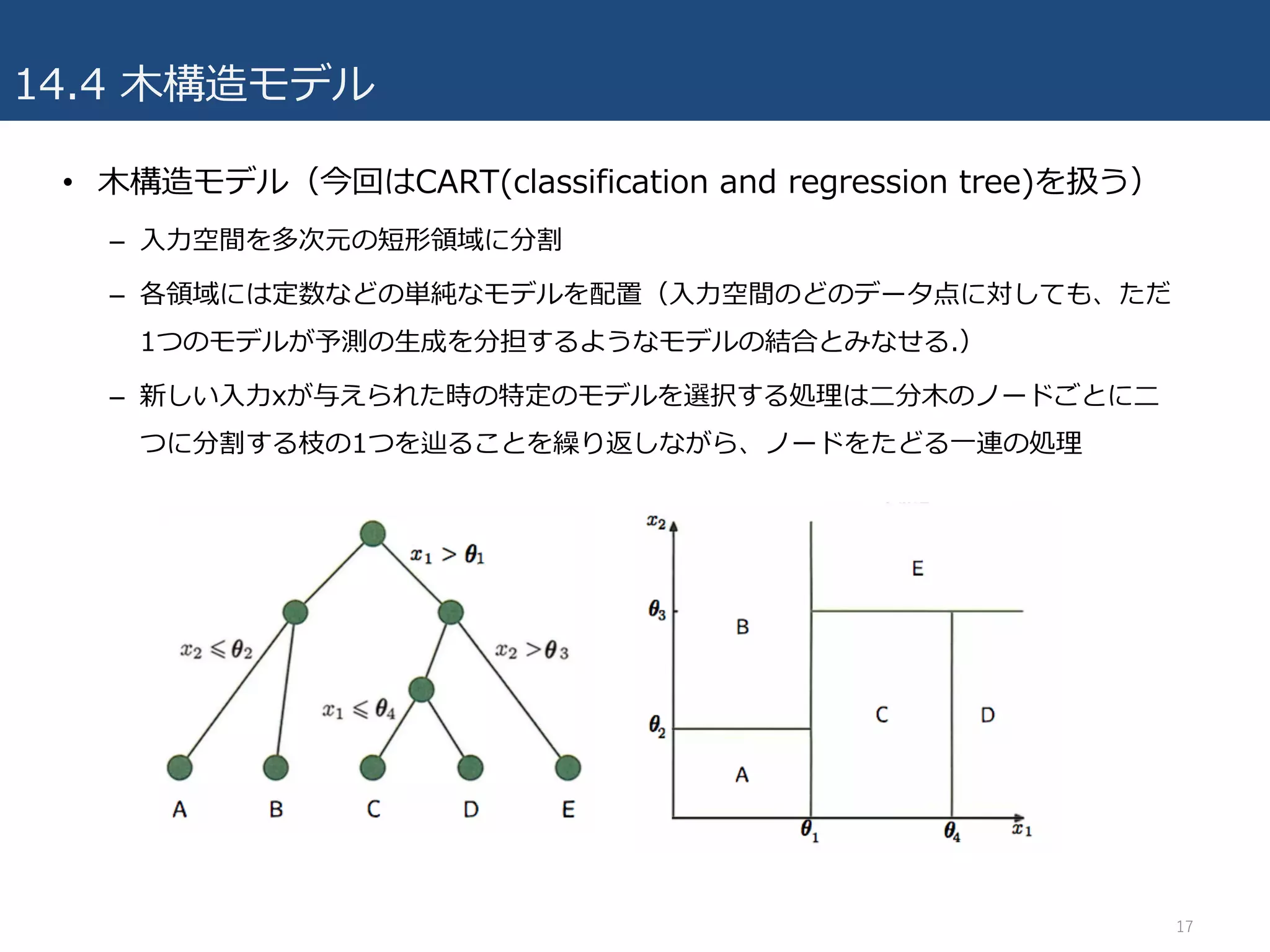
17. 14.4 ⽊構造モデル
• ⽊構造モデル（今回はCART(classification and regression tree)を扱う）
– ⼊⼒空間を多次元の短形領域に分割
– 各領域には定数などの単純なモデルを配置（⼊⼒空間のどのデータ点に対しても、ただ
1つのモデルが予測の⽣成を分担するようなモデルの結合とみなせる.）
– 新しい⼊⼒xが与えられた時の特定のモデルを選択する処理は⼆分⽊のノードごとに⼆
つに分割する枝の1つを辿ることを繰り返しながら、ノードをたどる⼀連の処理
17

18. 14.4 ⽊構造モデル
• D次元ベクトルx=(x1,…,xd)Tの⼊⼒変数から⼀次元の⽬標変数tを予測する
回帰問題を考える.
– 訓練データは, {t1,…,tN},{x1,…,xN}のセット. 既に⼊⼒空間の分割が与えられた上で、
⼆乗和誤差関数を最⼩化するなら、与えられたどの領域においても、予測変数の最適値
は、その領域の中にあるデータ点tnの平均値になる.(演習14.10)
18

19. 14.4 ⽊構造モデル
• 分割の構造の決め⽅
– 構造の組合せ（各分割における⼊⼒変数の選択やそでのしきい値設定含む）が膨⼤で計
算量的に難しい.
– → 単⼀のrootノードから貪欲最適化をする⽅法がよく使われる.
– 各ステップにおける処理（ノードの追加）、を繰り返す
• D個の⼊⼒変数から分割に⽤いる変数を選択
• しきい値を設定
– いつノードの追加を終わらせるか
• 「残差が⼀定以下になったら⽌める」⽅法はうまくいかない
– 誤差が全然減らないけど、そのまま分割を勧めていくと誤差が⼤きく減るケースが経験的に知られ
ている
• → 葉ノードのデータ点の数を基準(停⽌基準)に⽊を成⻑させ、最後に枝刈りする.
19

20. 14.4 ⽊構造モデル
• 枝刈りは、残差とモデルの複雑さに関する尺度のバランスに基いて⾏われる
• 枝刈りの⽅法
– 枝刈り前の⽊ T0
– 枝刈り後の⽊ T ⊂ T0
– 葉ノード γ = 1,…,|T|, 対応する領域Rγ（Nγ個のデータ点を持つ）
– 領域Rγに対する最適な予測：
– 対応する残差の寄与：
– 枝刈りの基準：
• γは, 交差確認法で選ばれる. 残差とモデルの複雑さのトレードオフ.
20

21. 14.4 ⽊構造モデル
• 分類問題の場合
– 誤差の尺度が変わる以外は同じ
• よく使われる⼆つの誤差の尺度
– １．交差エントロピー誤差関数
– ２．ジニ係数
– 領域Rγ内でクラスkに割り当てられるデータ点の割合pγk, k=1,…,K.
– どちらの尺度もpγk=0とpγk=1の時に値は0になり、pγk=0.5のときに最⼤値になる. →
特定の領域内でのデータ点が、⾼い⽐率で１つのクラスに割り当てられるようにした
い！
21

22. 14.4 ⽊構造モデル
• ⽊構造モデルの利点
– 学習が⾼速
– ⼈による可読性が⾼い
• ⽊構造モデルの⽋点
– 予測精度がそれほど良くない
– データ集合の細部に敏感（すぎる）
• 訓練データのわずかな変化で分割結果が⼤きく変わる
– 分割が特徴空間の軸に沿うので準最適になる（軸に対して45度な判別境界が最適である
場合、その最適な軸に平⾏でない分割に対して、多くの軸に平⾏な分割が必要になって
しまう。。）
– （回帰問題では、）滑らかな関数をモデル化するのが普通なのに、⽊モデルでは、予測
が分類境界ごとに定数予測で、不連続な予測値になってしまう。
22

23. 14.5 条件付混合モデル
• これまで
– 決定⽊は特徴空間の軸に沿ったハードな分割に制限される
• 本節
– 各分割において, １つの⼊⼒変数ではなく, 全ての⼊⼒変数を考慮した関数によるソフ
トな確率的な分割を⾏う（それにより↑の制限緩和できる）
• ただし, 決定⽊であった解釈可能性は消える
• 葉ノードのモデルを確率的に解釈すると, 完全に確率的な⽊構造モデル(階層的混合エキス
パートモデル. 詳細14.5.3)になる.
23

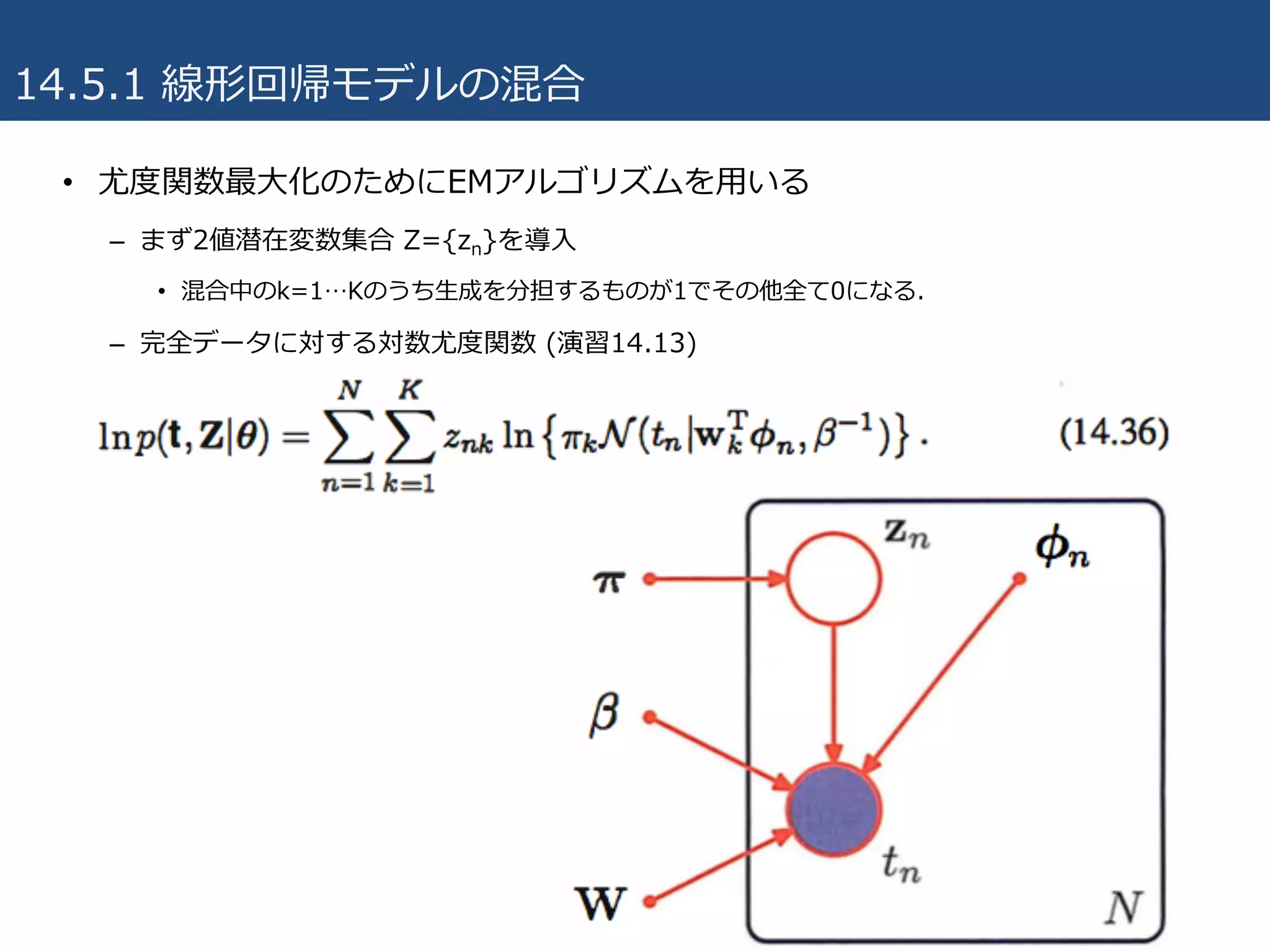
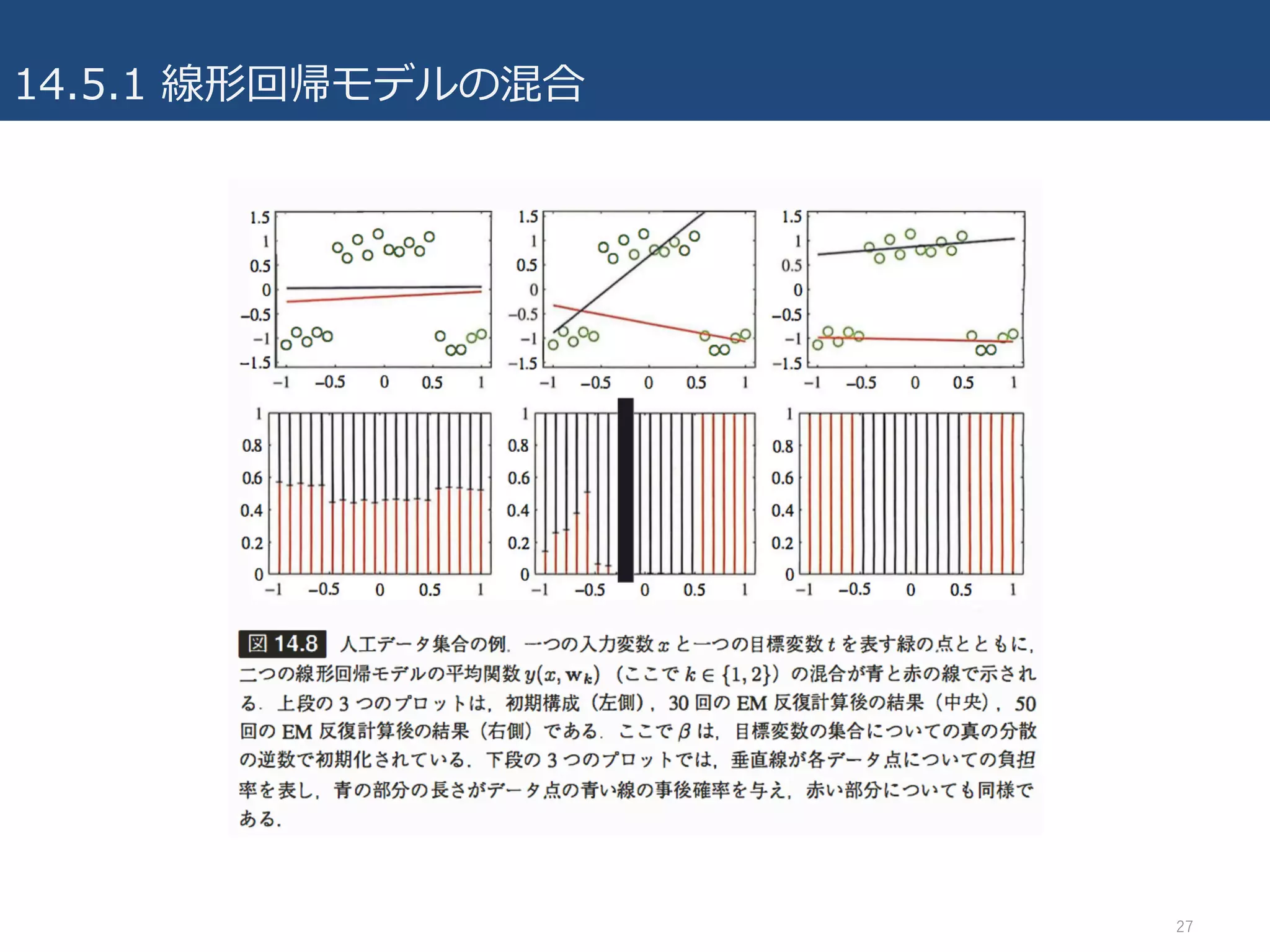
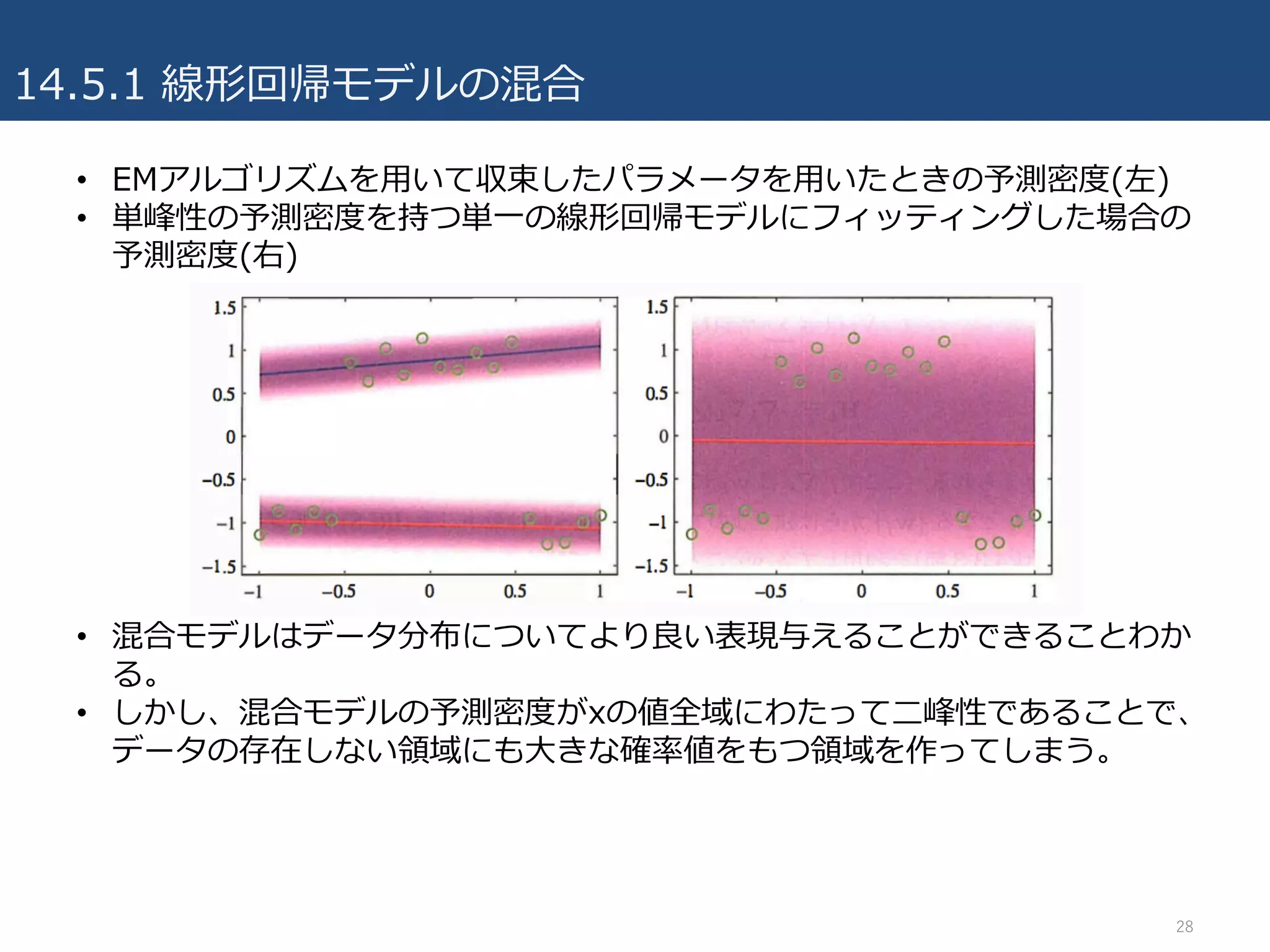
24. 14.5.1 線形回帰モデルの混合
• 線形回帰モデルを確率的に解釈することの利点の⼀つは、 より複雑な確率
モデルの基本的な構成要素として利⽤できる点。
• 9.2節で議論した混合ガウスモデルを、条件付ガウス分布に拡張することに
相当。
• それぞれが重みパラメータwkで⽀配されるK個の線形回帰モデルを考える.
– ⽬標変数tは1次元とする(複数出⼒への拡張は 演習14.12)
– 混合係数πk
– 混合分布は次のようになる.
• θはW={wk}, π={πk}, βをまとめて表したパラメータの集合
– 観測集合{φn, tn}が与えられた時の対数尤度関数
24

25. 14.5.1 線形回帰モデルの混合
• 尤度関数最⼤化のためにEMアルゴリズムを⽤いる
– まず2値潜在変数集合 Z={zn}を導⼊
• 混合中のk=1…Kのうち⽣成を分担するものが1でその他全て0になる.
– 完全データに対する対数尤度関数 (演習14.13)
25

26. 14.5.1 線形回帰モデルの混合
• (続き) EMアルゴリズム
– モデルパラメータとして最初に初期値θoldを選ぶことで開始
– Eステップ：↑のパラメータ値を⽤いて全てのデータ点nに対する各構成要素kの事後確
率すなわち負担率を求める.
– 負担率を⽤いて事後分布p(Z|t,θold)の下での完全データの対数尤度の期待値を計算す
る.
– Mステップ：γnk固定で、関数Q(θ, θold)をθに関して最⼤化. (θは, π, w, βまとめたパラ
メータ集合)
• 制約条件 のもと, ラグランジュ未定乗数法により,
• wkについて解ける(途中式省略):
– ロジスティック回帰の⽂脈での更新式(4.99)と同じ形
• βについても解ける:
26

27. 14.5.1 線形回帰モデルの混合
27

28. 14.5.1 線形回帰モデルの混合
28
• EMアルゴリズムを⽤いて収束したパラメータを⽤いたときの予測密度(左)
• 単峰性の予測密度を持つ単⼀の線形回帰モデルにフィッティングした場合の
予測密度(右)
• 混合モデルはデータ分布についてより良い表現与えることができることわか
る。
• しかし、混合モデルの予測密度がxの値全域にわたって⼆峰性であることで、
データの存在しない領域にも⼤きな確率値をもつ領域を作ってしまう。

29. 14.5.2 ロジスティックモデルの混合
• 混合ロジスティック回帰モデル
– ロジスティック回帰モデル(4.3節)の混合モデルver.
– K個のロジスティック回帰モデルによる⽬標変数の条件付き分布
• k番⽬の構成要素の出⼒:
– 尤度関数
29

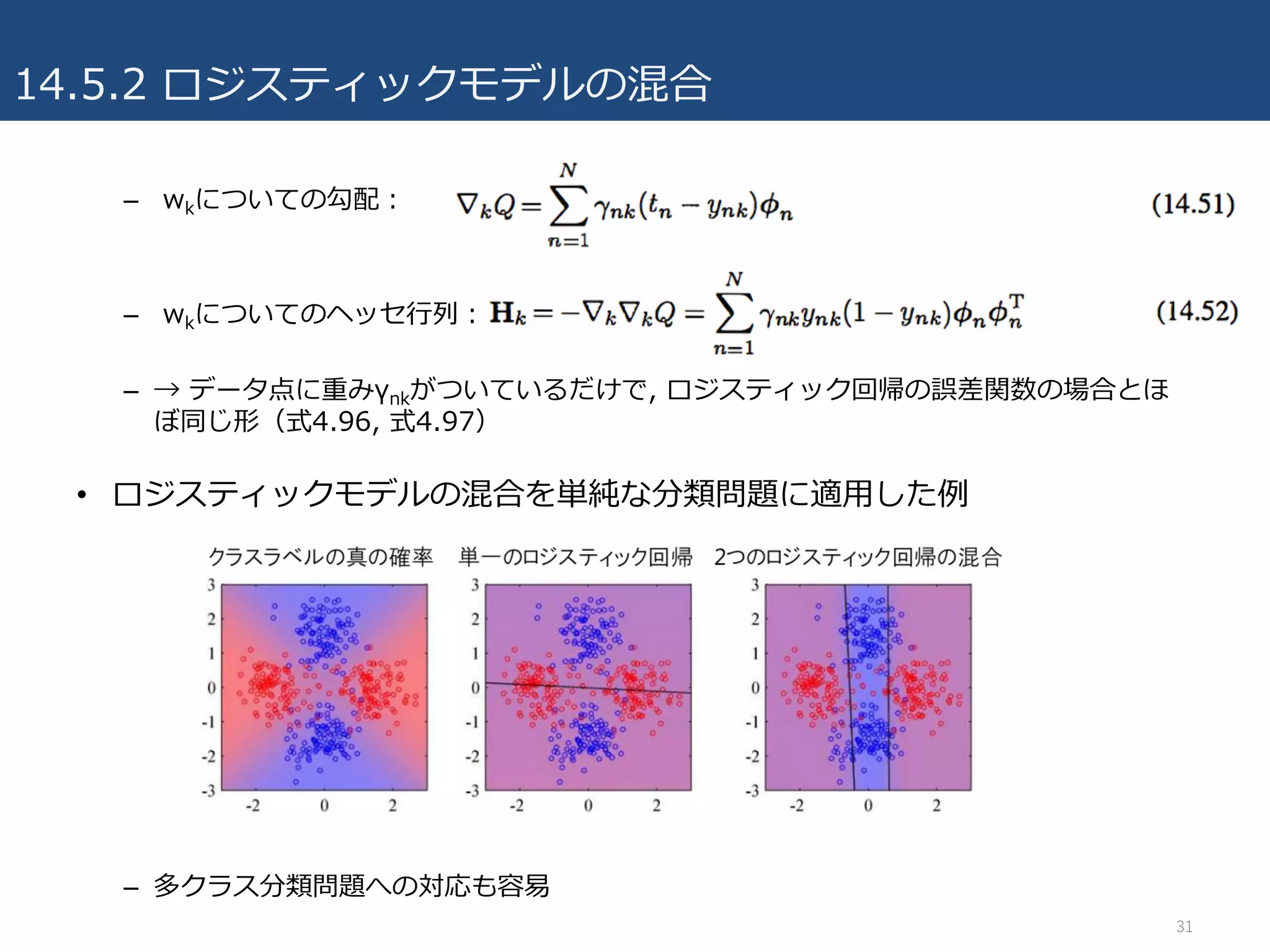
30. 14.5.2 ロジスティックモデルの混合
• 線形回帰モデルと同様, 2値の潜在変数znkを導⼊してEMアルゴリズムで尤度
関数最⼤化を⾏う.
– 完全データでの尤度関数
• Eステップ：負担率の計算.
• Mステップ：Q関数のパラメータに関する最⼤化.
– πkに関して最⼤化(同様に)
– wkに関して最⼤化 → 閉じた式にならないので反復計算する
• 反復重み付け最⼩⼆乗(IRLS)アルゴリズムなどを利⽤(4.3.3節)
30

31. 14.5.2 ロジスティックモデルの混合
– wkについての勾配：
– wkについてのヘッセ⾏列：
– → データ点に重みγnkがついているだけで, ロジスティック回帰の誤差関数の場合とほ
ぼ同じ形（式4.96, 式4.97）
• ロジスティックモデルの混合を単純な分類問題に適⽤した例
– 多クラス分類問題への対応も容易
31

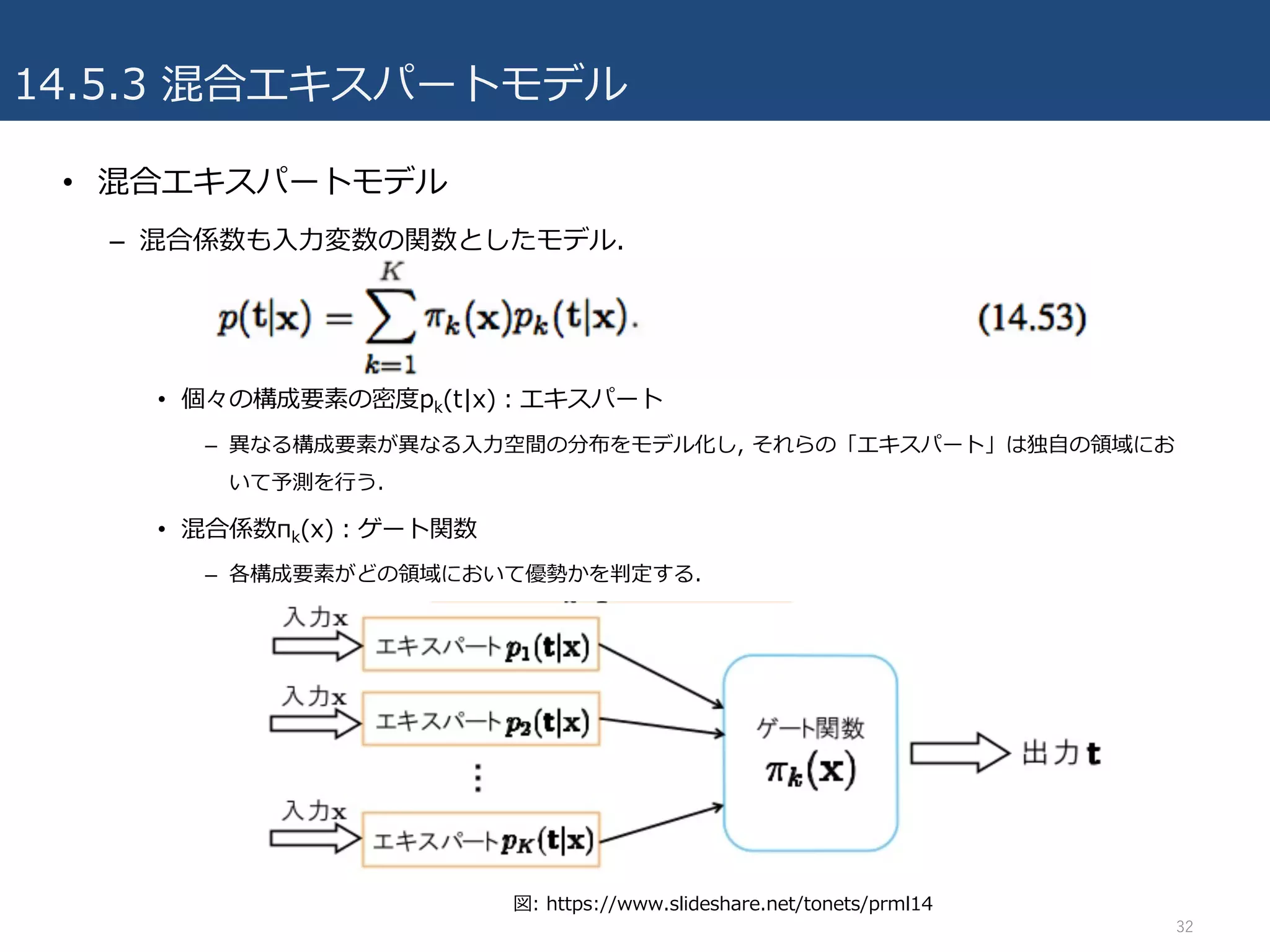
32. 14.5.3 混合エキスパートモデル
• 混合エキスパートモデル
– 混合係数も⼊⼒変数の関数としたモデル.
• 個々の構成要素の密度pk(t|x)：エキスパート
– 異なる構成要素が異なる⼊⼒空間の分布をモデル化し, それらの「エキスパート」は独⾃の領域にお
いて予測を⾏う.
• 混合係数πk(x)：ゲート関数
– 各構成要素がどの領域において優勢かを判定する.
32
図: https://www.slideshare.net/tonets/prml14

33. 14.5.3 混合エキスパートモデル
• ゲート関数の制約
– 確率値であるため.
– 例えば, 線形ソフトマックスモデルで表現できる.
– エキスパートも線形モデルなら, Mステップで最⼩⼆乗法を利⽤するEMアルゴリズムに
より, モデル全体を効率よくフィットできる.
33

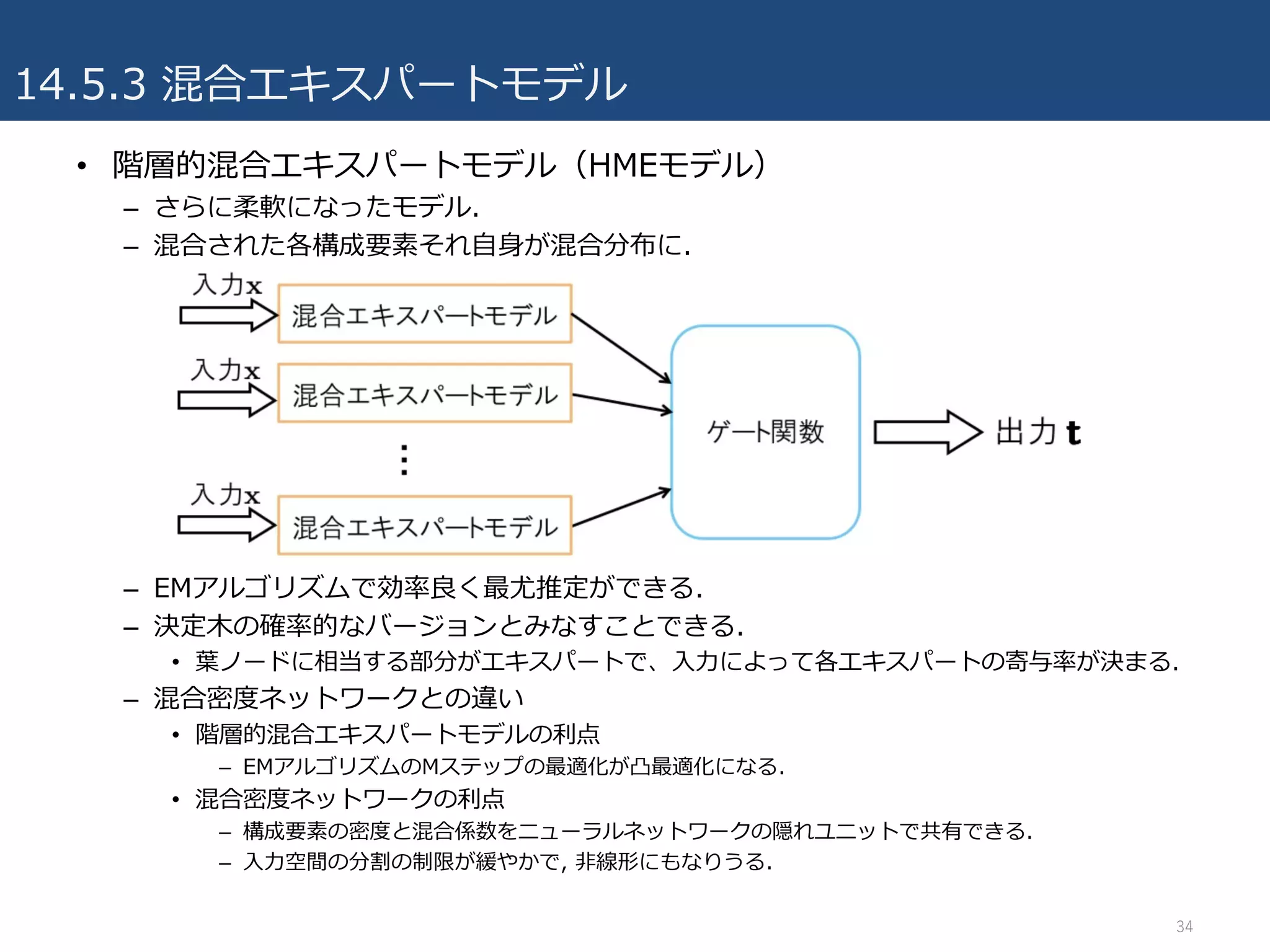
34. 14.5.3 混合エキスパートモデル
• 階層的混合エキスパートモデル（HMEモデル）
– さらに柔軟になったモデル.
– 混合された各構成要素それ⾃⾝が混合分布に.
– EMアルゴリズムで効率良く最尤推定ができる.
– 決定⽊の確率的なバージョンとみなすことできる.
• 葉ノードに相当する部分がエキスパートで、⼊⼒によって各エキスパートの寄与率が決まる.
– 混合密度ネットワークとの違い
• 階層的混合エキスパートモデルの利点
– EMアルゴリズムのMステップの最適化が凸最適化になる.
• 混合密度ネットワークの利点
– 構成要素の密度と混合係数をニューラルネットワークの隠れユニットで共有できる.
– ⼊⼒空間の分割の制限が緩やかで, ⾮線形にもなりうる.
34

35. 参考
• パターン認識と機械学習 下 (ベイズ理論による統計的予測)
– C.M. ビショップ (著), 元⽥ 浩 (監訳), 栗⽥ 多喜夫 (監訳), 樋⼝ 知之 (監訳), 松本 裕
治 (監訳), 村⽥ 昇 (監訳)
• PRML Chapter 14（Masahito Ohue, SlideShare）
– https://www.slideshare.net/tonets/prml14
• PRML 第14章（Akira Morizawa, SlideShare）
– https://www.slideshare.net/pecorarista/prml-14
• PRML 14章（ぱんいちすみもと, SlideShare）
– https://www.slideshare.net/ssuser9eb780/prml-14-75527511
• Prml14 5（正志 坪坂, SlideShare）
– https://www.slideshare.net/tsubosaka/prml14-5
35