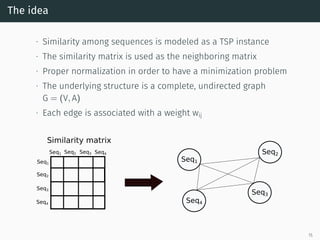
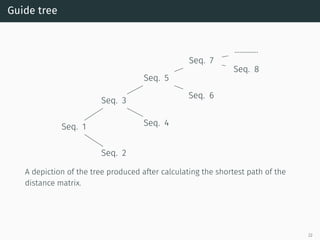
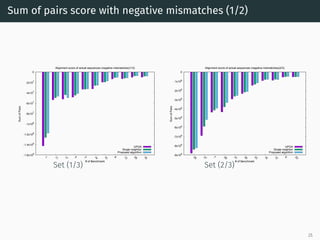
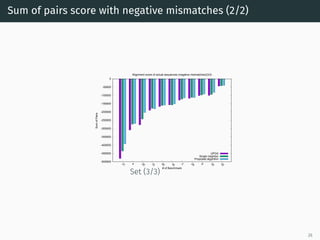
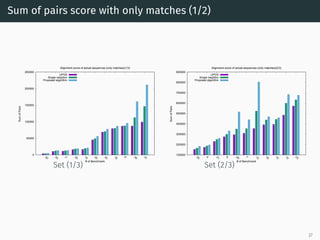
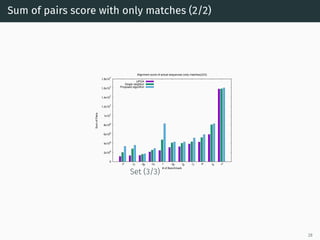
The document presents a quantum-inspired heuristic for solving the multiple sequence alignment problem in bioinformatics. It models the sequence similarity as a traveling salesman problem instance using a normalized similarity matrix. The method applies a quantum-inspired generalized variable neighborhood search metaheuristic to approximate the shortest Hamiltonian path and generate an initial alignment. Evaluation on real biological sequences shows it outperforms progressive methods, producing alignments with good sum-of-pairs scores, especially for large sequence sets.

1. A quantum-inspired optimization heuristic for
the multiple sequence alignment problem in
bio-computing
10th International Conference on Information, Intelligence, Systems and Ap-
plications (IISA 2019)
Patras, Greece
Konstantinos Giannakis, Christos Papalitsas, Georgia Theocharopoulou, Sofia
Fanarioti, and Theodore Andronikos
July 15-17, 2019
Dept. of Informatics, Ionian University, Greece
kgiann@ionio.gr

2. Acknowledgment
This research is funded in the context of the project “Investigating alternative computational
methods and their use in computational problems related to optimization and game theory,” (MIS
5007500) under the call for proposals “Supporting researchers with an emphasis on young
researchers” (EDULL34). The project is co-financed by Greece and the European Union (European
Social Fund - ESF) by the Operational Programme Human Resources Development, Education and
Lifelong Learning 2014-2020.
1

3. Project info
∙
∙ Natural and biomolecular computing
∙ Modeling with Membrane automata
∙ Unconventional Computational Methods
∙ Quantum Optimization Algorithms and Strategies
→http://di.ionio.gr/alcomopt/←
2

4. An overview
◎ Biological Sequences
◎ Alignment
∙ Single and multiple alignment (MSA)
◎ NP-hard for most cases
◎ Bio-inspired techniques
◎ Translate the MSA problem as a TSP instance
∙ Proposal of a quantum-inspired method
∙ To progressively solve this problem
∙ Evaluated through simulations against other aligning methods
∙ Provide a good initial alignment, especially for large sets of
sequences
3

5. Background

6. Introduction
∙ Biological sequences play an important role in various fields
✓ The multiple sequence alignment or MSA considers the problem
of aligning a set of sequences
∙ They usually represent proteins or nucleotides
∙ Pairwise alignment → 2 sequences
∙ Related to non-biological fields, e.g., in information-related
fields, natural language processing, finances, etc.
 NP-complete with SP-score and NP-hard for most metrics
∙ Global and local alignments
∙ Usually dynamic programming approaches
- Heuristic and/or probabilistic methods for larger instances
5

7. Motivaton
∙ Arranging sequences of DNA, RNA, or proteins in order to study
properties and relationships among themselves
∙ Useful in many fields → it can reveal interesting properties
about the sequences (e.g., phylogenetic trees)
∙ Sequences are usually large and multitudinous
∙ Need for good alignments within acceptable time frames, at
least for an initial solution
6

8. Pairwise and multiple alignment
∙ Examples: sequences S1 = ACTTAA and S2 = CAGTAC:
A C T - T A A -
- C A G T A - C
∙ If you add an extra sequence S3 = CGGACA:
A C T - T A A - -
- C A G T A - C -
- C G G - A - C A
7

9. Solutions and methods
∙ Progressive, iterative, motif-based, and hybrid methods
✓ Progressive: the most similar sequences are aligned first and
then the rest of them are aligned in a decreasing order
∙ Various scoring functions (e.g., sum-of-pairs metric, the
weighted sum-of-pairs, etc.)
∙ Quantum- and bio-inspired approaches1,2,3
∙ Trying to take advantage of the superiority of quantum
computing
1
A. Perdomo-Ortiz et al. “Finding low-energy conformations of lattice protein models by
quantum annealing”. In: Scientific reports 2 (2012), p. 571.
2
D-Wave Initiates Open Quantum Software Environment. D-Wave Systems.
3
L. Abdesslem et al. “Multiple sequence alignment by quantum genetic algorithm”. In: |
Proceedings 20th International Parallel & Distributed Processing Symposium. IEEE. 2006, p. 360.
8

10. Other approaches
∙ Needleman–Wunsch algorithm for global pairwise alignment
(dynamic programming; O(n2
) complexity)
∙ Smith–Waterman algorithm for local pairwise alignment
∙ Platforms: MUSCLE, Multalin, CLUSTALs (Omega)
∙ Multalin: a progressive approach based on the UPGMA,
∙ CLUSTAL W: a progressive approach based upon the
neighbor-joining (NJ) algorithm
∙ Both UPGMA and (NJ) require the construction of a complete
distance matrix of the sequences
9

11. Related literature and quantum computation
∙ Quantum computing4
∙ D-WAVE
∙ Neven’s law
∙ Quantum algorithms for pattern-matching5
and sequence
comparison problems6
∙ A quantum-inspired genetic algorithm for MSA7
∙ Combining TSP with MSA8,9
4
M. A. Nielsen and I. L. Chuang. Quantum Computation and Quantum Information. Cambridge
University Press, 2010.
5
A. Sarkar. “Quantum Algorithms: for pattern-matching in genomic sequences”. In: (2018).
6
L. C. Hollenberg. “Fast quantum search algorithms in protein sequence comparisons:
Quantum bioinformatics”. In: Physical Review E 62.5 (2000), p. 7532.
7
Hong-Wei Huo et al. “A quantum-inspired genetic algorithm based on probabilistic coding for
multiple sequence alignment”. In: Journal of bioinformatics and computational biology 8.01
(2010), pp. 59–75.
8
J.D. Banda-Tapia et al. “Optimizing multiple sequence alignments using traveling salesman
problem and order-based evolutionary algorithms”. In: Proceedings of CIBB 2 (2012).
9
C. Korostensky and G. Gonnet. “Using traveling salesman problem algorithms for evolutionary
tree construction”. In: Bioinformatics 16.7 (2000), pp. 619–627.
10

12. Main part

13. Notation
∙ Σ = {s1, s2, .., sm} a finite alphabet; a sequence is a string over Σ
∙ Two sequences S′
1 and S′
2 are alignments of two sequences S1
and S2 if S′
i can be obtained from Si by removing gaps
∙ This holds for more sequences, too
∙ m: the max length of sequences S′
1 and S′
2
∙ The total cost for this alignment can be expressed as
m∑
i=1
d(S′
1(i), S′
2(i))
∙ d is the chosen scoring function
∙ S′
j (i) is the ith character of sequence S′
j
12

14. Scoring functions
∙ A standard score scheme:
d(S′
1(i), S′
2(i)) =
{
1, if match
0, if mismatch
∙ An optimal alignment is the one with the maximum score
∙ The matrix of size n × m represents an alignment of the n
sequences
A C T - T A A - -
- C A G T A - C -
- C G G - A - C A
∙ Several scoring schemes
∙ The most widely used → sum of pairs
13

15. Sum of pairs
∙
(mn
2
)
total pairs
n−1∑
i=1
n∑
j=i+1
d(Si, Sj)
∙ Can “punish” mismatches, e.g., by giving -1 to any mismatch
∙ Examples: sequences S1 = ACTTAA and S2 = CAGTAC:
A C T - T A A -
- C A G T A - C
∙ The score for this alignment is 3
A C T - T A A - -
- C A G T A - C -
- C G G - A - C A
∙ The score for the above alignment is 9
14

16. The idea
∙ Similarity among sequences is modeled as a TSP instance
∙ The similarity matrix is used as the neighboring matrix
∙ Proper normalization in order to have a minimization problem
∙ The underlying structure is a complete, undirected graph
G = (V, A)
∙ Each edge is associated with a weight wij
15

17. The proposed method

18. Our approach
∙ We apply the qGVNS quantum-inspired metaheuristic10
∙ It consists of a VND local search, a diversification procedure,
and a neighborhood change step
∙ VNS and GVNS have bio-inspired origins
∙ Novelty: In qGVNS, a modified diversification phase successfully
resolves local minima traps by exploiting quantum computation
techniques
∙ A simulated quantum register generates a complex
n-dimensional unit vector during each shaking call
∙ The complex n-dimensional vector is fed as input and outputs a
real n-dimensional vector
∙ The i-th component of the real vector is equal to the modulus
squared of the i-th component of the complex vector
10
Christos Papalitsas et al. “Combinatorial GVNS (General Variable Neighborhood Search)
Optimization for Dynamic Garbage Collection”. In: Algorithms 11.4 (2018), p. 38.
17

19. The qGVNS routine
Data: an initial solution
Result: an optimized solution
1 Initialization of the feasibility distance matrix
2 begin
3 X ← Nearest Neighbor heuristic;
4 repeat
5 X′
← Quantum-Perturbation(X)
6 X′′
← pipeVND(X′
)
7 if X′′
is better than X′
then
8 X ← X′′
9 end
10 until optimal solution is found or time limit is met;
11 end
18

20. The proposed method
Data: a set of sequences
Result: a set of aligned sequences
1 Disti,j: The pairwise distance matrix of the sequences
2 begin
3 i ← the i-th sequence
4 j ← the j-th sequence
5 repeat
6 Disti,j ← Calculate pairwise distance of i-th and j-th
sequences
7 until all pairs are examined;
8 end
9 Sol ← Approximation of the shortest Hamiltonian of Dist ▷ Derived
using qGVNS of Algorithm 1
10 Score_matrix ▷ Choose a score matrix of your choice
11 Gap_penalty ▷ Choose the value of gap penalty
12 Align sequences following the Sol matrix as guide
19

21. In a nutshell
∙ Initial calculation of the distance matrix among the sequences
∙ This is a trivial part for most MSA algorithms
∙ The choices for a score matrix and a gap penalty do not affect
the main algorithm
✓ They can be separately chosen
∙ It enhances its applicability
20

22. Analysis
∙ Need for the calculation of pairwise distances of the sequences
∙ Exhaustive comparisons
∙ Calculation of the complete distance matrix
∙ For n sequences, this calculation requires O(m(n2
− n))
comparisons (m is the maximum length)
∙ The calculation of the shortest Hamiltonian path is a known
NP-hard problem
 It seems like the proposed algorithm simply hides the “hard”
computational part
✓ This is not true, though, since the GVNS-based heuristic only
approximates the solution in a specific time frame
∙ After the qGVNS, the actual alignment is straightforward through
a simple (binary) guide tree from the above resulting ordering
21

23. Guide tree
Seq. 1
Seq. 2
Seq. 3
Seq. 4
Seq. 5
Seq. 6
Seq. 7
Seq. 8
.............
A depiction of the tree produced after calculating the shortest path of the
distance matrix.
22

24. Results

25. Evaluation
∙ Benchmarked on 33 real sequences retrieved from NCBI
∙ Samples from different kinds of organisms were chosen
(archaea, invertebrates, plants, and plasmids)
∙ MatLab
∙ For the first set, each match is scored with 1, whereas any
mismatch is scored with -1
∙ For the second set, no negative score for mismatches
∙ Compared against UPGMA and single neighbor algorithm
24

26. Sum of pairs score with negative mismatches (1/2)
-1.6x108
-1.4x10
8
-1.2x108
-1x10
8
-8x107
-6x107
-4x107
-2x107
0
1
11
17
5
2
14
10
8
13
26
19
SumofPairs
# of Benchmark
Alignment score of actual sequences (negative mismatches)(1/3)
UPGA
Single neighbor
Proposed algorithm
Set (1/3)
-9x106
-8x106
-7x106
-6x106
-5x106
-4x10
6
-3x106
-2x10
6
-1x106
0
29
27
7
28
31
30
23
16
12
6
22
SumofPairs
# of Benchmark
Alignment score of actual sequences (negative mismatches)(2/3)
UPGA
Single neighbor
Proposed algorithm
Set (2/3)
25

27. Sum of pairs score with negative mismatches (2/2)
-500000
-450000
-400000
-350000
-300000
-250000
-200000
-150000
-100000
-50000
0
21
4
25
15
20
18
3
24
9
33
32
SumofPairs
# of Benchmark
Alignment score of actual sequences (negative mismatches)(3/3)
UPGA
Single neighbor
Proposed algorithm
Set (3/3)
26

28. Sum of pairs score with only matches (1/2)
0
50000
100000
150000
200000
250000
32
24
3
20
15
22
33
18
9
30
31
SumofPairs
# of Benchmark
Alignment score of actual sequences (only matches)(1/3)
UPGA
Single neighbor
Proposed algorithm
Set (1/3)
100000
200000
300000
400000
500000
600000
700000
800000
900000
25
4
21
6
29
7
13
16
12
10
23
SumofPairs
# of Benchmark
Alignment score of actual sequences (only matches)(2/3)
UPGA
Single neighbor
Proposed algorithm
Set (2/3)
27

29. Sum of pairs score with only matches (2/2)
0
2x106
4x106
6x10
6
8x106
1x10
7
1.2x107
1.4x10
7
1.6x107
1.8x107
5
17
28
27
1
26
19
11
8
14
2
SumofPairs
# of Benchmark
Alignment score of actual sequences (only matches)(3/3)
UPGA
Single neighbor
Proposed algorithm
Set (3/3)
28

30. Result overview
∙ Better suited for larger sequences
∙ All algorithms operate under the progressive alignment scheme
∙ They, too, use the full distance matrix
∙ All use the same method for pairwise alignment
✓ The proposed algorithm outperforms the other two
∙ Especially when larger sets of sequences are used
∙ No prior knowledge on the relation among the sequences was
assumed
29

31. Concluding

32. Conclusion
 Biology and bioinformatics are related to demanding problems
 MSA is an indicative example
 Many approaches and scoring methods
 We followed the progressive approach
 A quantum-inspired optimization heuristic
 Evaluated on actual sets of sequences from NCBI
 We provide alignments with good scores, especially when the
sets of sequences are large
 Useful for constructing an initial alignment
 If prior knowledge is available?
 Decrease cost upon the distance matrix
31

33. Key References I
L. Abdesslem et al. “Multiple sequence alignment by quantum genetic algorithm”. In: |
Proceedings 20th International Parallel & Distributed Processing Symposium. IEEE. 2006,
p. 360.
J.D. Banda-Tapia et al. “Optimizing multiple sequence alignments using traveling salesman
problem and order-based evolutionary algorithms”. In: Proceedings of CIBB 2 (2012).
D-Wave Initiates Open Quantum Software Environment. D-Wave Systems.
L. C. Hollenberg. “Fast quantum search algorithms in protein sequence comparisons:
Quantum bioinformatics”. In: Physical Review E 62.5 (2000), p. 7532.
Hong-Wei Huo et al. “A quantum-inspired genetic algorithm based on probabilistic coding
for multiple sequence alignment”. In: Journal of bioinformatics and computational biology
8.01 (2010), pp. 59–75.
C. Korostensky and G. Gonnet. “Using traveling salesman problem algorithms for
evolutionary tree construction”. In: Bioinformatics 16.7 (2000), pp. 619–627.
M. A. Nielsen and I. L. Chuang. Quantum Computation and Quantum Information.
Cambridge University Press, 2010.
32

34. Key References II
Christos Papalitsas et al. “Combinatorial GVNS (General Variable Neighborhood Search)
Optimization for Dynamic Garbage Collection”. In: Algorithms 11.4 (2018), p. 38.
A. Perdomo-Ortiz et al. “Finding low-energy conformations of lattice protein models by
quantum annealing”. In: Scientific reports 2 (2012), p. 571.
A. Sarkar. “Quantum Algorithms: for pattern-matching in genomic sequences”. In: (2018).
33

35.   
Thank you for your attention!
34

36. Any Questions?
35