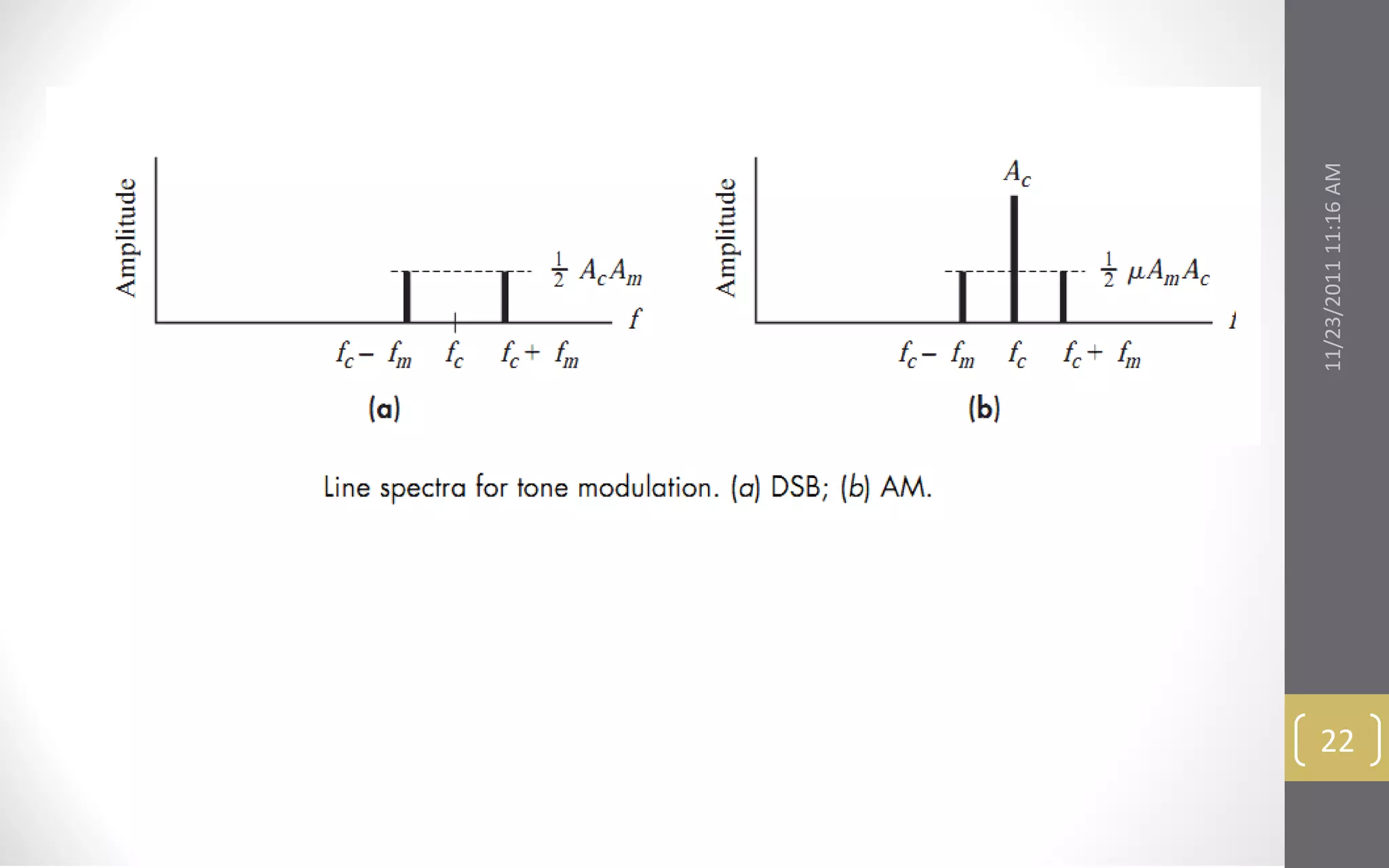
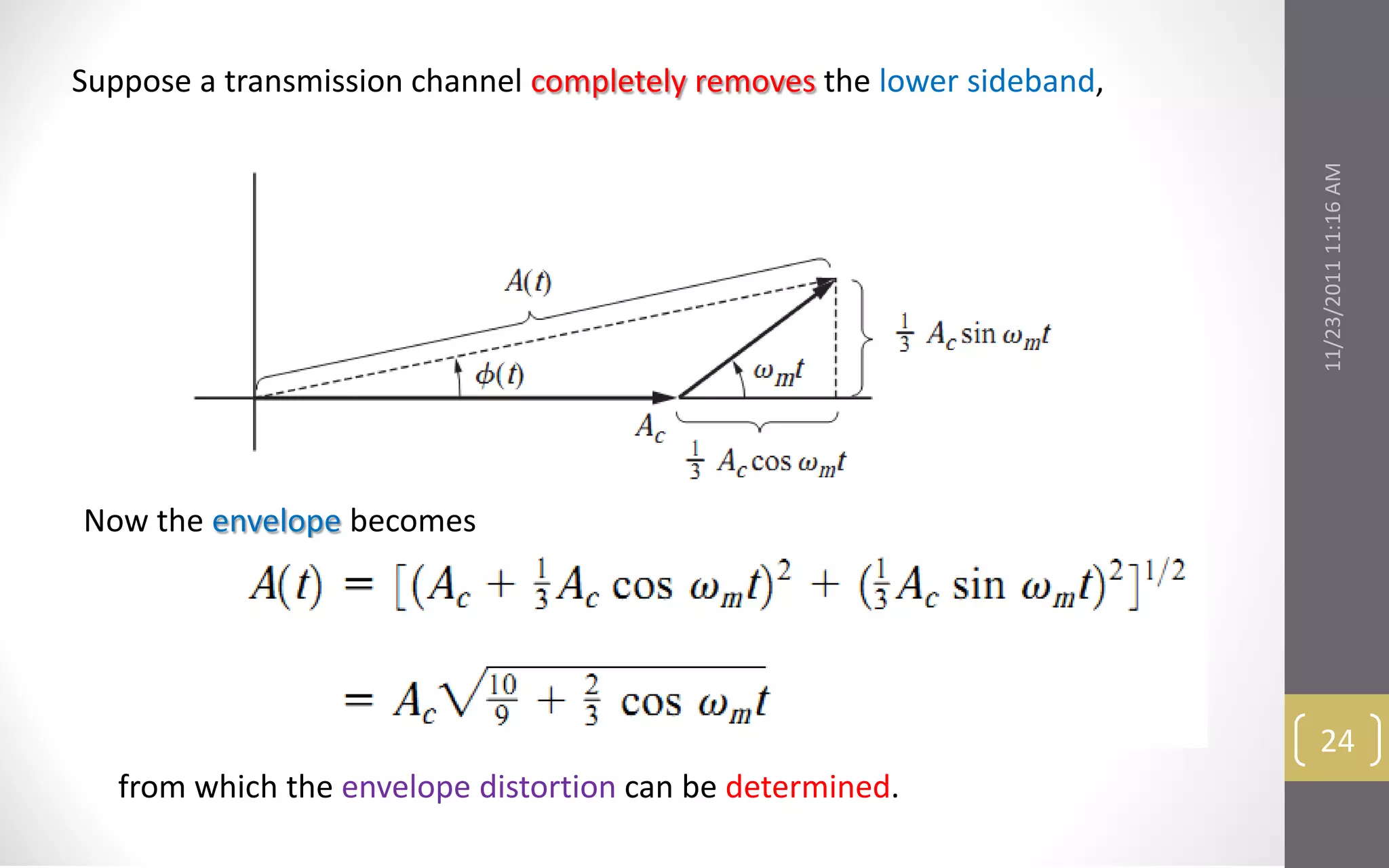
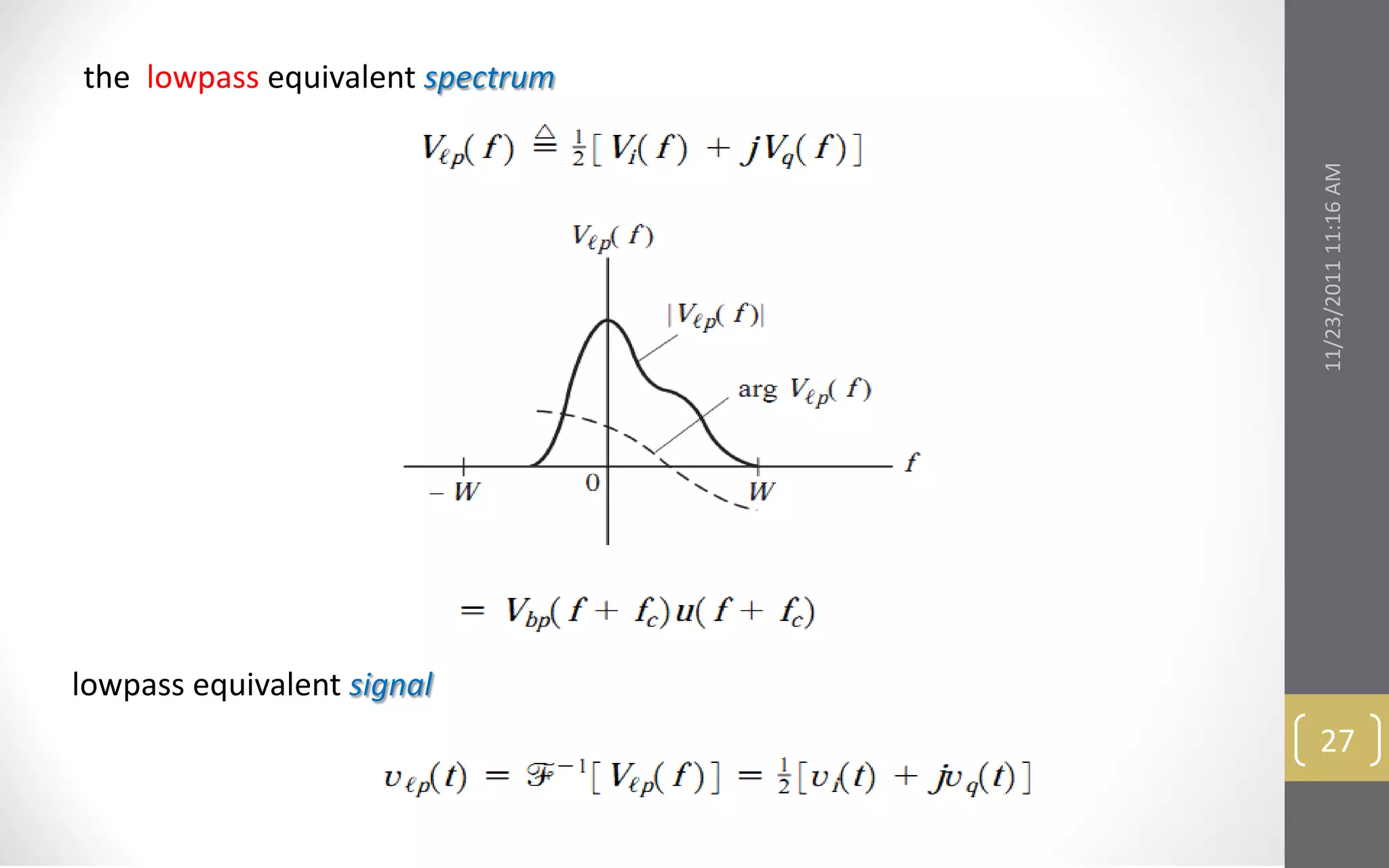
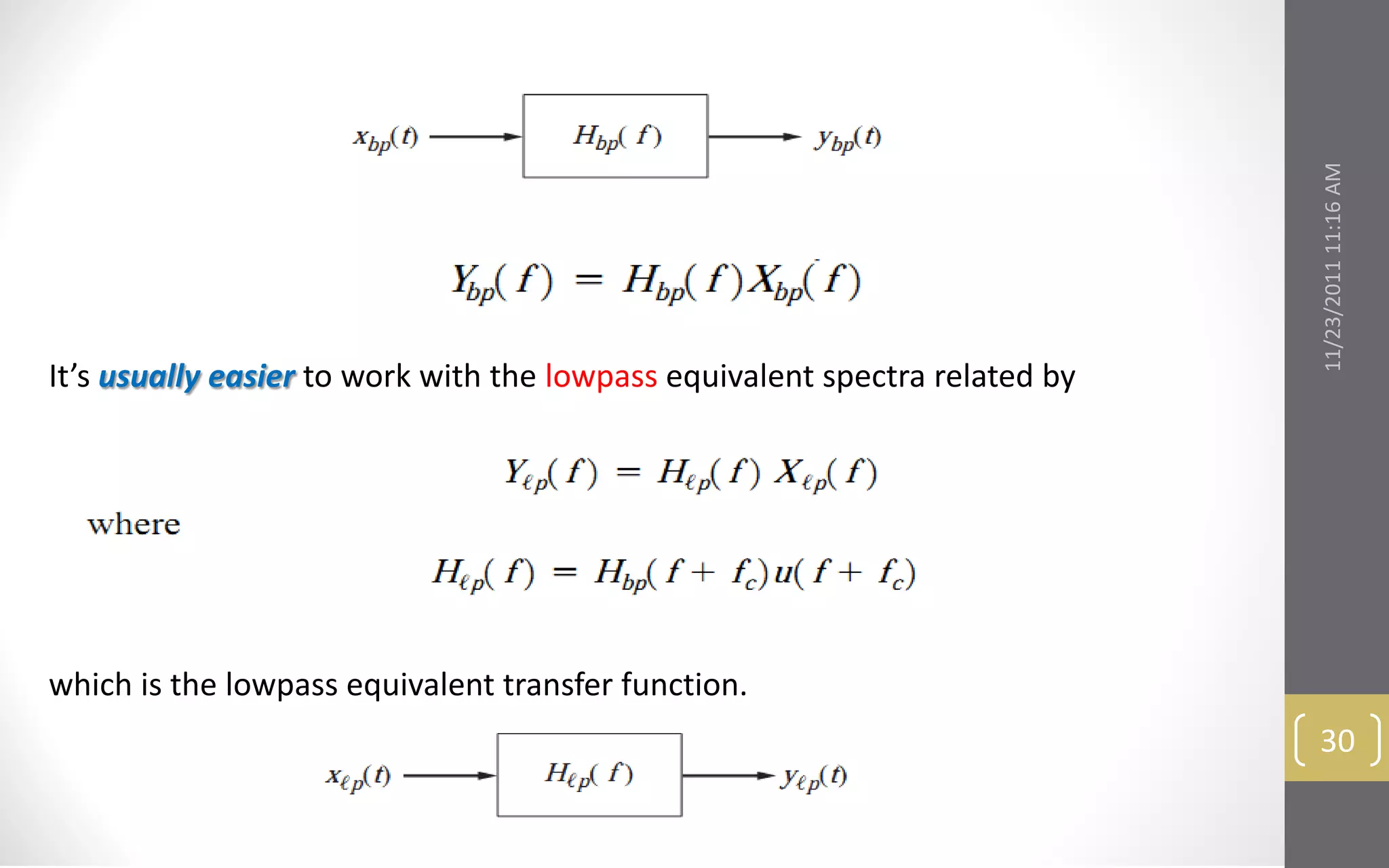
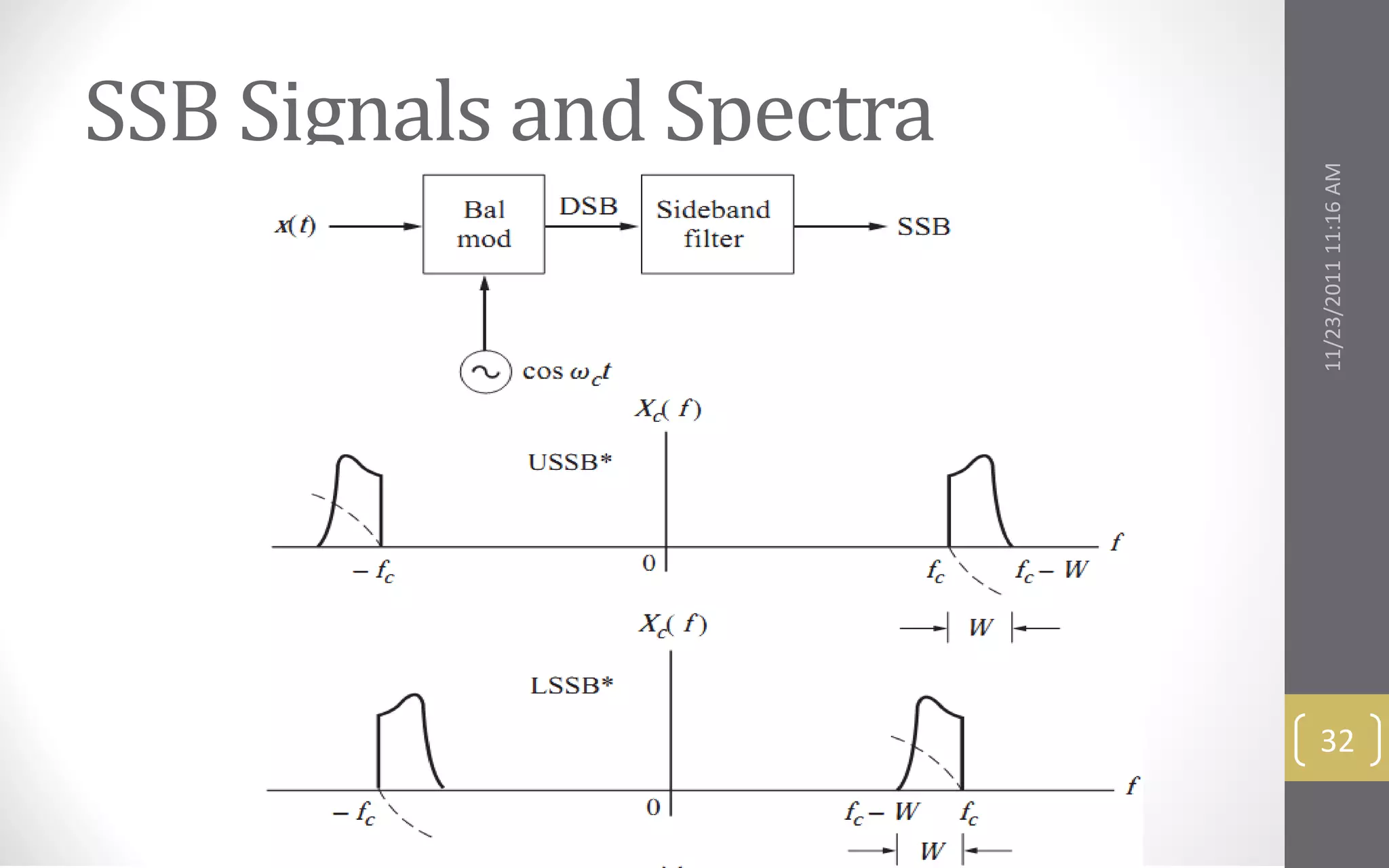
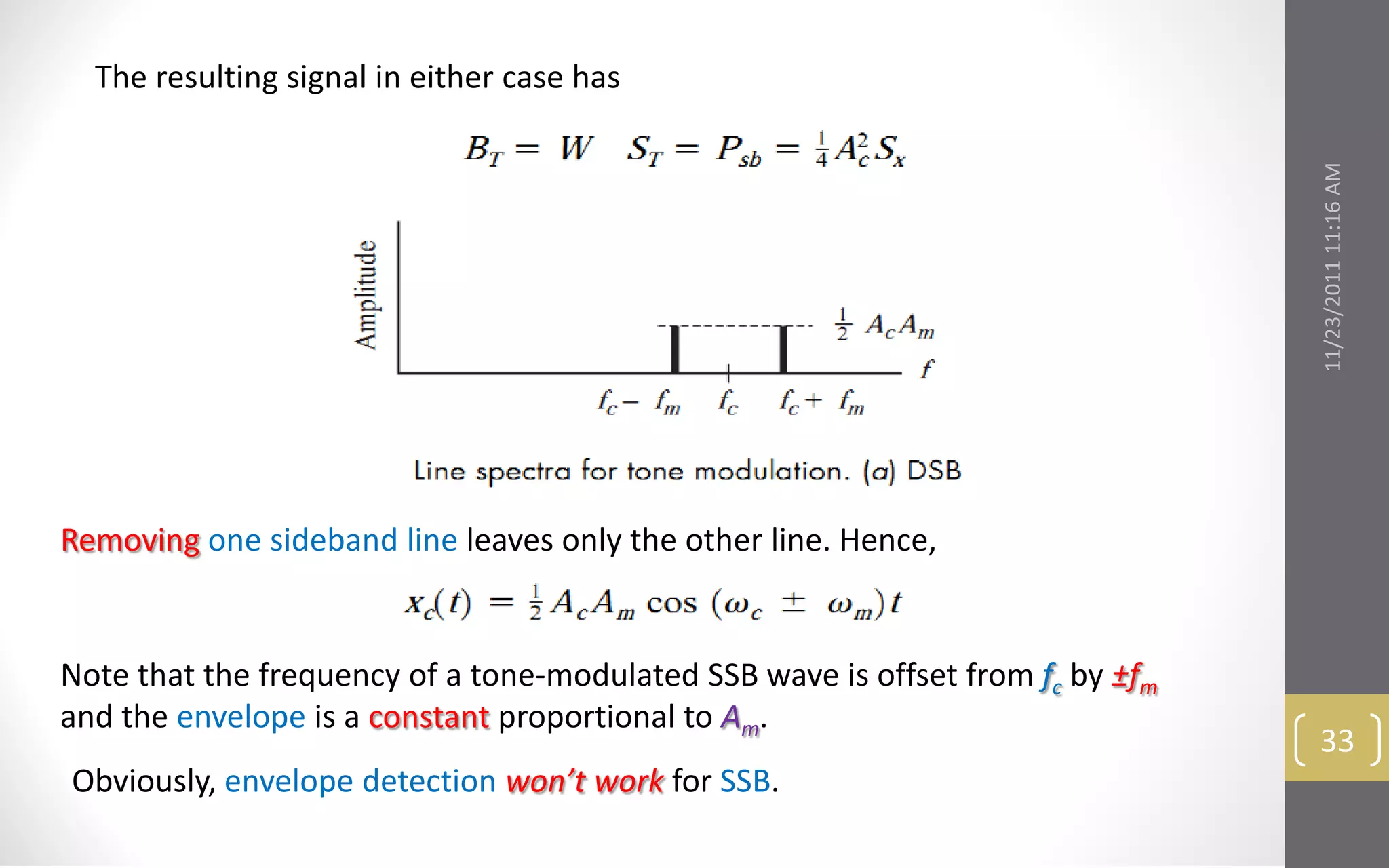
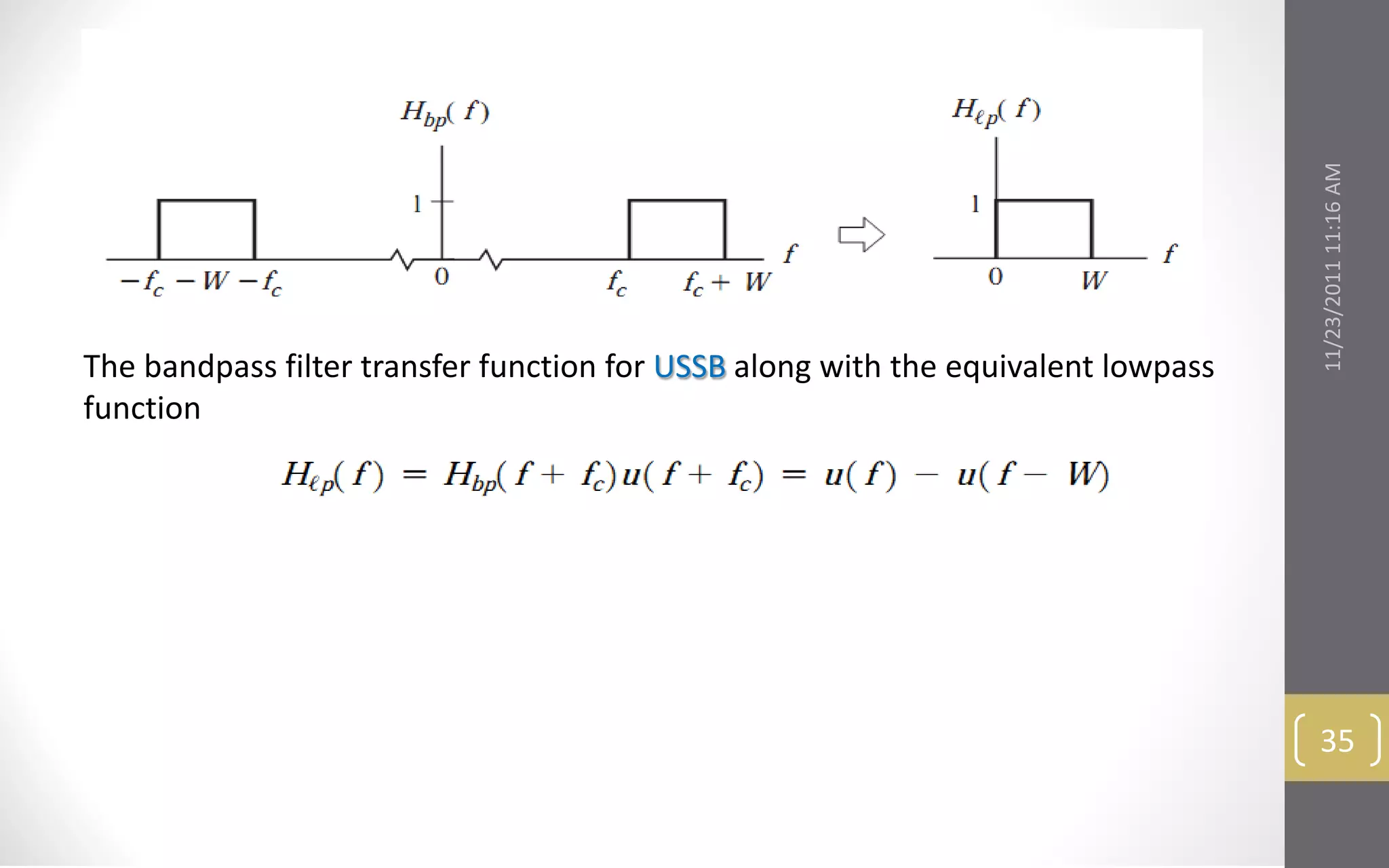
This document provides an overview and roadmap for the topics covered in the linear CW modulation course. The topics include: bandpass signals and systems, double sideband amplitude modulation, modulators and transmitters, suppressed sideband amplitude modulation, and frequency conversion and demodulation. It outlines the key concepts that will be discussed under each topic.

1. Linear CW Modulation

2. Roadmap
11/23/2011 11:16 AM
1. Bandpass Signals and Systems
2. Double-Sideband Amplitude Modulation
3. Modulators and Transmitters
4. Suppressed-Sideband Amplitude Modulation
5. Frequency Conversion and Demodulation
2

3. BANDPASS SIGNALS AND SYSTEMS
11/23/2011 11:16 AM
• Analog Message Conventions
• Bandpass Signals
• Bandpass Transmission
• Bandwidth
3

4. Analog Message Conventions
11/23/2011 11:16 AM
sinusoidal or tone modulation
4

5. Bandpass Signals
5
11/23/2011 11:16 AM

6. 11/23/2011 11:16 AM
envelope-and-phase description
where A(t) is the envelope and φ(t) is the phase, both functions of time
The envelope is defined as nonnegative, so that A(t) ≥ 0 . Negative “amplitudes,”
6
when they occur, are absorbed in the phase by adding ±180o .

7. 11/23/2011 11:16 AM
in-phase
component quadrature
component
7
quadrature-carrier description

8. DOUBLE-SIDEBAND AMPLITUDE
11/23/2011 11:16 AM
MODULATION
• AM Signals and Spectra
• DSB Signals and Spectra
• Tone Modulation and Phasor Analysis
8

9. AM Signals and Spectra
11/23/2011 11:16 AM
If Ac denotes the unmodulated carrier amplitude, modulation by x(t) produces the
AM signal
modulation
index
The signal’s envelope is
xc(t) has no time-varying phase, its in-phase and quadrature components are
9

10. 11/23/2011 11:16 AM
10

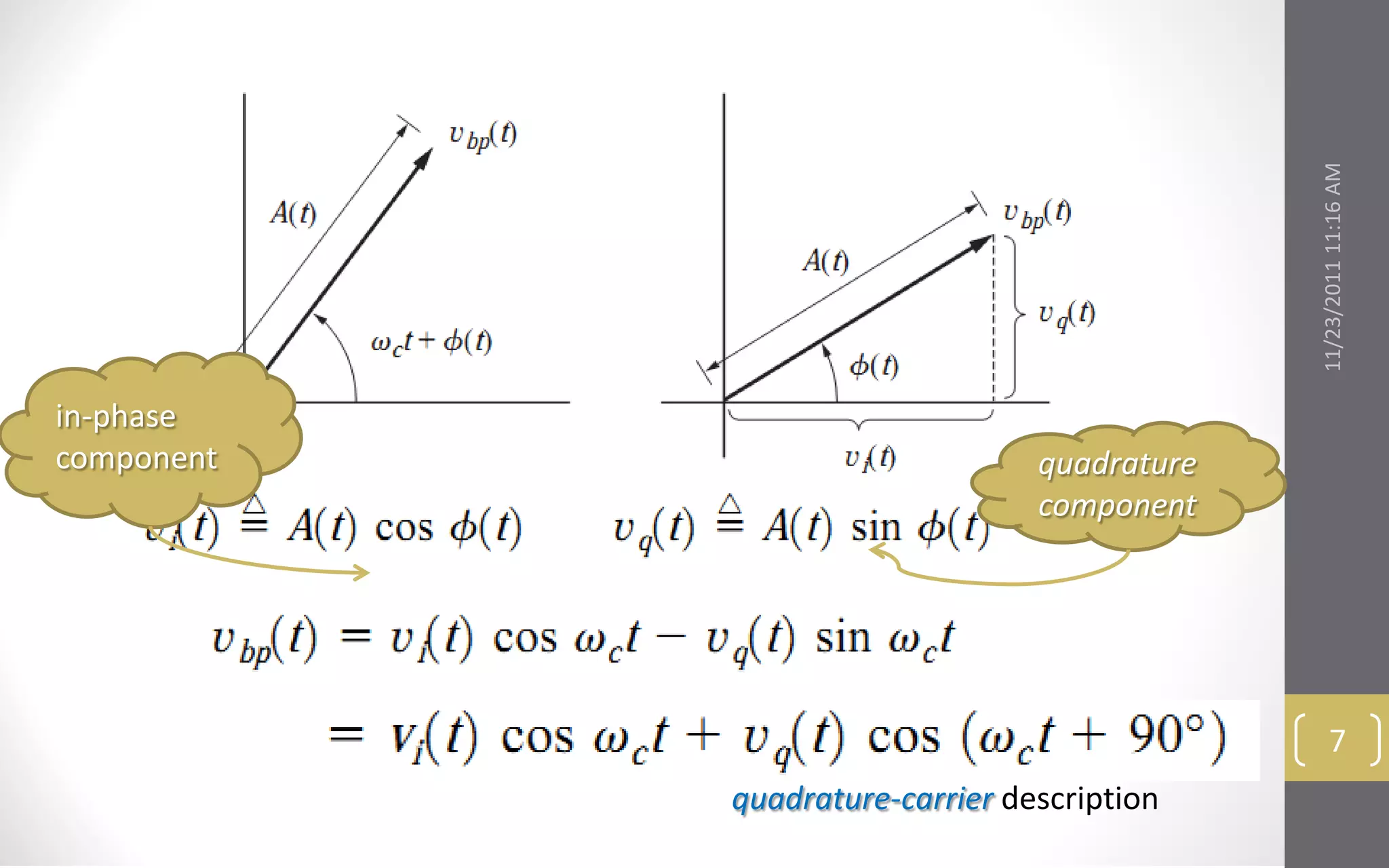
11. The envelope clearly reproduces the shape of if
11/23/2011 11:16 AM
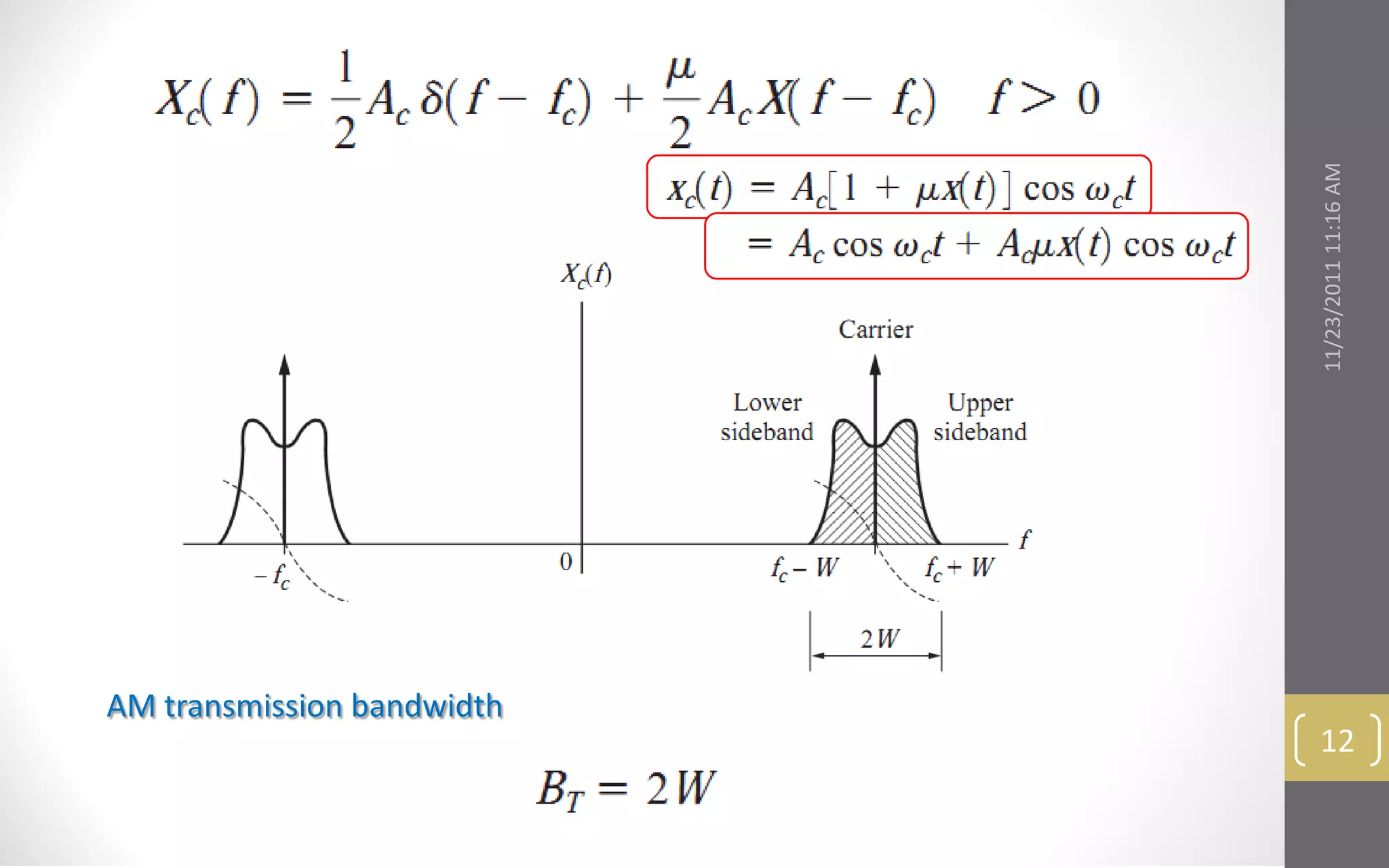
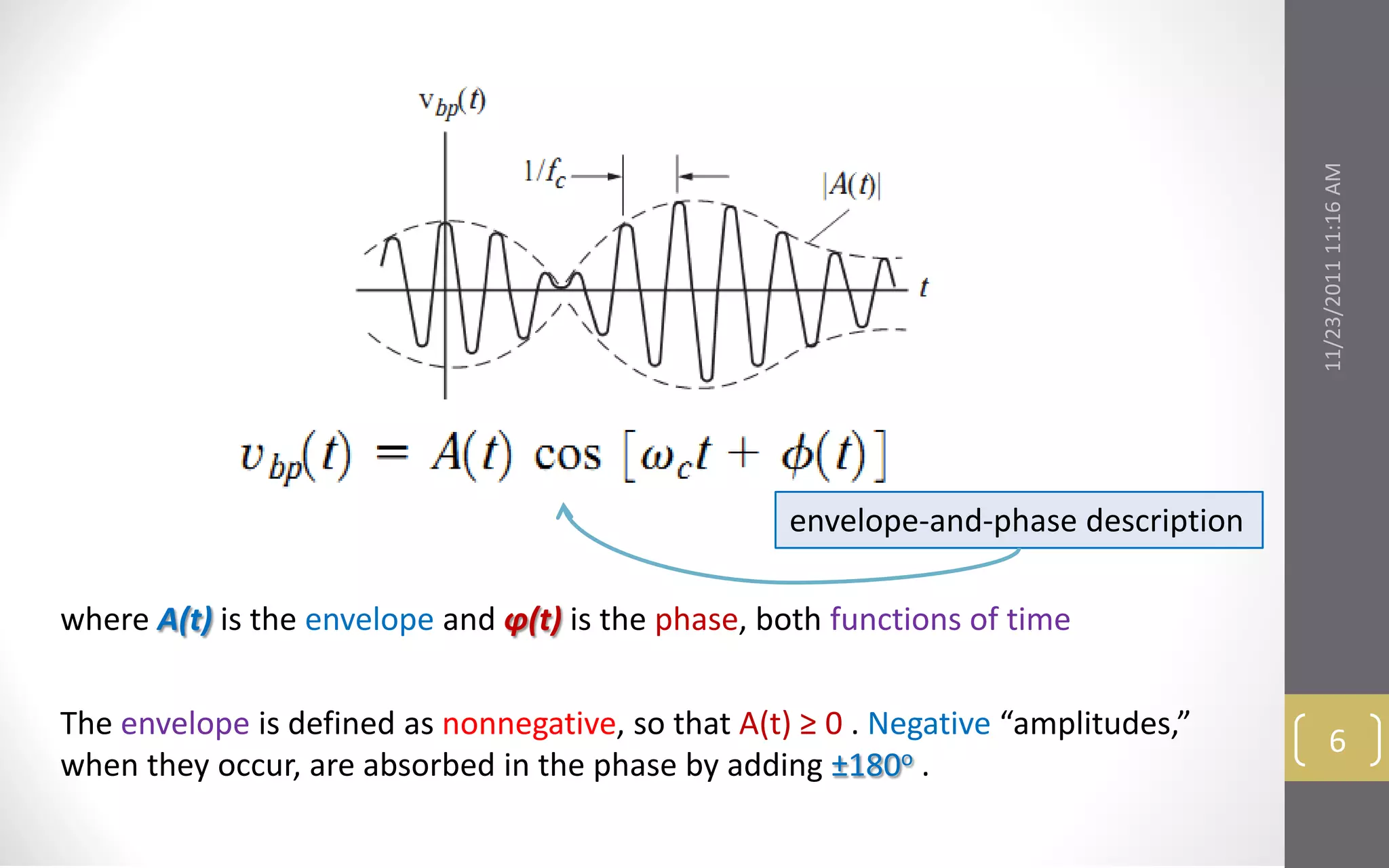
The condition fc >> W ensures that the carrier oscillates rapidly compared to the
time variation of x(t); otherwise, an envelope could not be visualized.
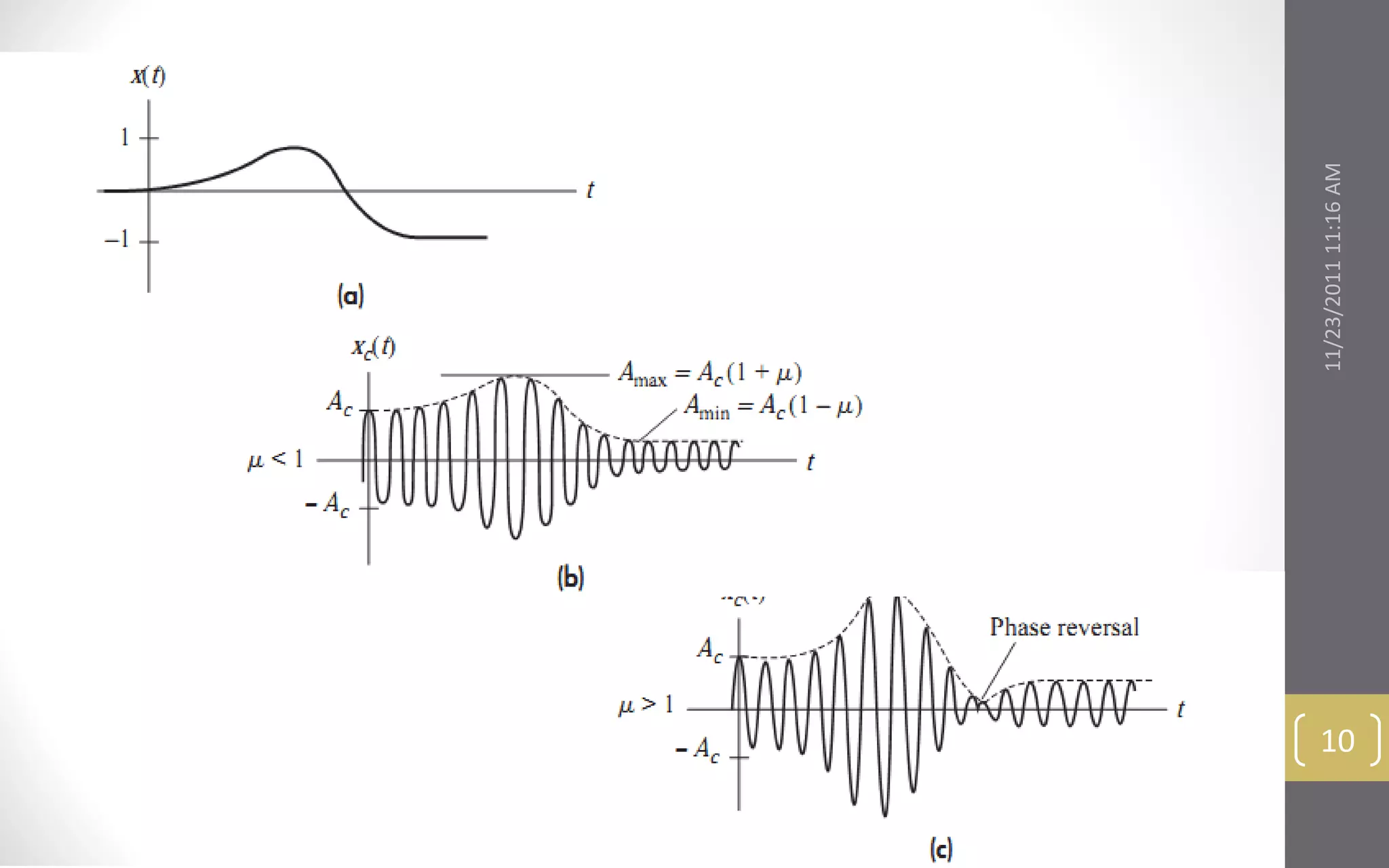
The condition μ ≤ 1 ensures that Ac[ 1 + μx(t) ] does not go negative.
With 100 percent modulation (μ = 1), the envelope varies between Amin = 0
and Amax = 2Ac .
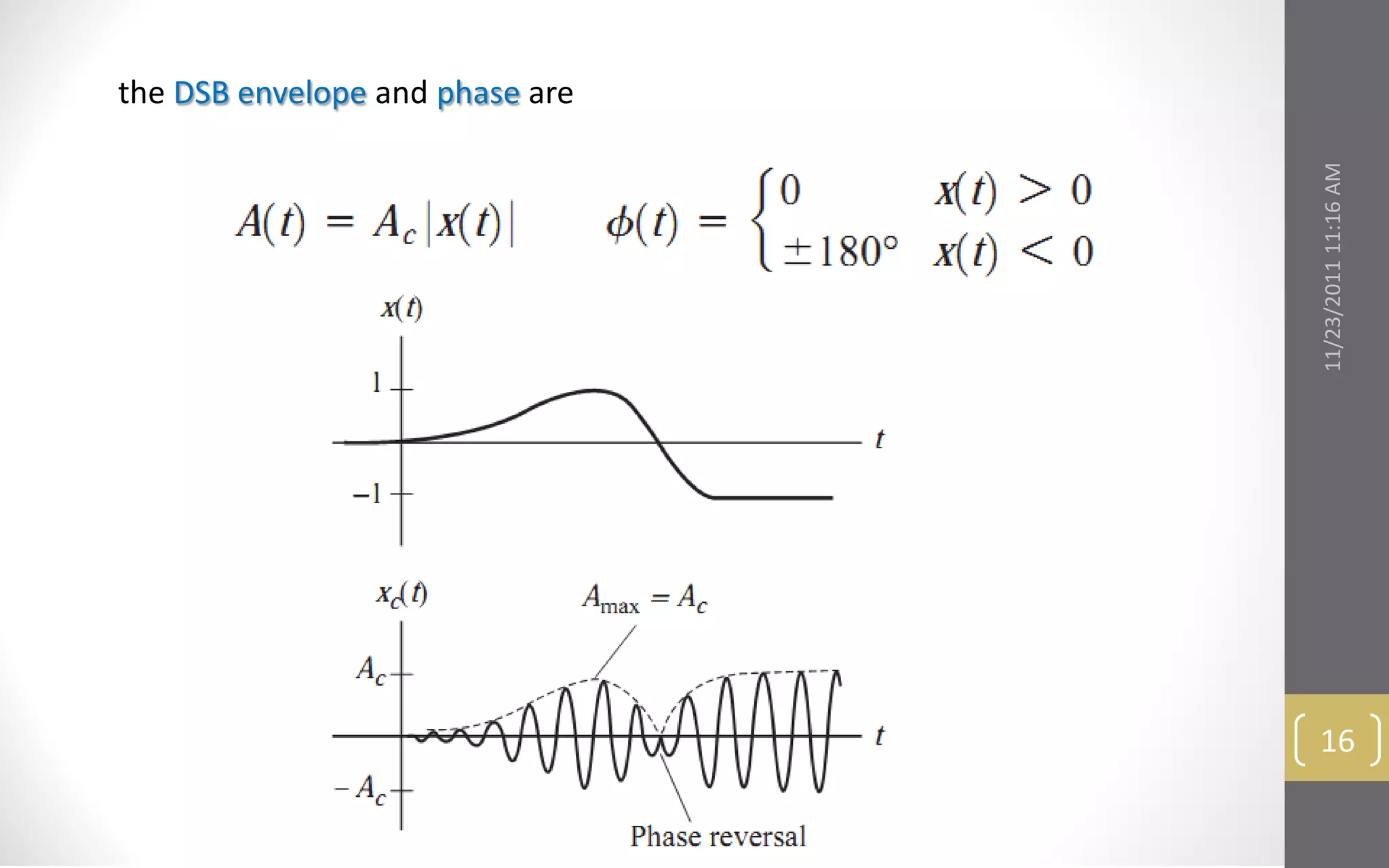
Overmodulation ( μ > 1), causes phase reversals and envelope distortion
11

12. 11/23/2011 11:16 AM
AM transmission bandwidth
12

13. Another important consideration is the average transmitted power
11/23/2011 11:16 AM
Upon expanding
averages to zero under the
condition fc >> W
13

14. The term Pc represents the unmodulated carrier power, since ST = Pc when μ = 0
11/23/2011 11:16 AM
the term Psb represents the power per sideband since, when μ ≠ 0, ST consists of
the power in the carrier plus two symmetric sidebands.
The modulation constraint
requires that
Consequently, at least 50 percent (and often close to 2/3) of the total transmitted
power resides in a carrier term that’s independent of and thus conveys no
message information.
14

15. DSB Signals and Spectra
11/23/2011 11:16 AM
The “wasted” carrier power in amplitude modulation can be eliminated by
setting and suppressing the unmodulated carrier-frequency component. The
resulting modulated wave becomes
which is called double-sideband–suppressed-carrier modulation—or DSB for
short. (The abbreviations DSB–SC and DSSC are also used.)
the DSB spectrum looks like an AM spectrum without the unmodulated carrier
impulses. The transmission bandwidth thus remains unchanged . 15

16. the DSB envelope and phase are
11/23/2011 11:16 AM
16

17. The envelope here takes the shape of |x(t)|, rather than x(t), and the modulated
wave undergoes a phase reversal whenever x(t) crosses zero.
11/23/2011 11:16 AM
Full recovery of the message requires knowledge of these phase reversals, and
could not be accomplished by an envelope detector.
Carrier suppression does put all of the average transmitted power into the
information-bearing sidebands.
Practical transmitters also impose a limit on the peak envelope power
We’ll take account of this peak-power limitation by examining the ratio
17

18. 11/23/2011 11:16 AM
DSB conserves power but requires
complicated demodulation circuitry,
whereas AM requires increased power
to permit simple envelope detection.
18

19. EXAMPLE Consider a radio transmitter rated for
11/23/2011 11:16 AM
Let the modulating signal be a tone with
If the modulation is DSB,
the maximum possible power per sideband equals the
lesser of the two values determined from
19

20. If the modulation is AM with μ = 1, then
11/23/2011 11:16 AM
To check on the average-power limitation,
Hence, the peak power limit again dominates and the maximum sideband
power is
Since transmission range is proportional to Psb , the AM path length would be 20
only 25 percent of the DSB path length with the same transmitter.

21. Tone Modulation and Phasor
Analysis
11/23/2011 11:16 AM
Setting
the tone-modulated DSB waveform
tone-modulated AM wave
21

22. 11/23/2011 11:16 AM
22

23. EXAMPLE: AM and Phasor Analysis
tone-modulated AM with
11/23/2011 11:16 AM
the phasor sum equals the envelope
23

24. Suppose a transmission channel completely removes the lower sideband,
11/23/2011 11:16 AM
Now the envelope becomes
24
from which the envelope distortion can be determined.

25. SUPPRESSED-SIDEBAND AMPLITUDE
11/23/2011 11:16 AM
MODULATION
• SSB Signals and Spectra
• SSB Generation
• VSB Signals and Spectra
25

26. 11/23/2011 11:16 AM
The in-phase and quadrature functions must be lowpass signals
26

27. the lowpass equivalent spectrum
11/23/2011 11:16 AM
lowpass equivalent signal
27

28. Rectangular-to-Polar conversion yields
11/23/2011 11:16 AM
The lowpass-to-bandpass transformation in the time domain.
The corresponding frequency-domain transformation is
28

29. Since we’ll deal only with real bandpass signals, we can keep the hermitian
symmetry, in mind and use the simpler expression
11/23/2011 11:16 AM
29

30. 11/23/2011 11:16 AM
It’s usually easier to work with the lowpass equivalent spectra related by
which is the lowpass equivalent transfer function.
30

31. In particular, after finding , you can take its inverse Fourier transform
11/23/2011 11:16 AM
The lowpass-to-bandpass transformation then yields the output signal
Or you can get the output quadrature components or envelope and phase
immediately from
31

32. SSB Signals and Spectra
11/23/2011 11:16 AM
32

33. The resulting signal in either case has
11/23/2011 11:16 AM
Removing one sideband line leaves only the other line. Hence,
Note that the frequency of a tone-modulated SSB wave is offset from fc by ±fm
and the envelope is a constant proportional to Am.
33
Obviously, envelope detection won’t work for SSB.

34. To analyze SSB with an arbitrary message x(t),
we’ll draw upon the fact that the sideband filter is a bandpass system with a
11/23/2011 11:16 AM
bandpass DSB input
and a bandpass SSB output
applying the equivalent lowpass method.
Since xbp(t) has no quadrature component, the lowpass equivalent input is simply
34

35. 11/23/2011 11:16 AM
The bandpass filter transfer function for USSB along with the equivalent lowpass
function
35

36. The corresponding transfer functions for LSSB are
11/23/2011 11:16 AM
Both lowpass transfer functions can be represented by
36

37. yields the lowpass equivalent spectrum for either USSB or LSSB, namely
11/23/2011 11:16 AM
Now recall that
Finally, we perform the lowpass-to-bandpass transformation
37

38. SSB Generation
11/23/2011 11:16 AM
38

39. VSB Signals and Spectra
11/23/2011 11:16 AM
39

40. Review Questions
11/23/2011 11:16 AM
40

41. Problems to Ponder
11/23/2011 11:16 AM
41

42. Review Questions
11/23/2011 11:16 AM
42

43. Problems to Ponder
11/23/2011 11:16 AM
43

44. MODULATORS AND TRANSMITTERS
11/23/2011 11:16 AM
• Product Modulators
• Square-Law and Balanced Modulators
• Switching Modulators
44

45. Product Modulators
11/23/2011 11:16 AM
45

46. Square-Law and Balanced
Modulators
11/23/2011 11:16 AM
46

47. Switching Modulators
11/23/2011 11:16 AM
47

48. Review Questions
11/23/2011 11:16 AM
48

49. Problems to Ponder
11/23/2011 11:16 AM
49

50. SUPPRESSED-SIDEBAND AMPLITUDE
11/23/2011 11:16 AM
MODULATION
• SSB Signals and Spectra
• SSB Generation
• VSB Signals and Spectra
50

51. SSB Signals and Spectra
11/23/2011 11:16 AM
51

52. SSB Generation
11/23/2011 11:16 AM
52

53. VSB Signals and Spectra
11/23/2011 11:16 AM
53

54. Review Questions
11/23/2011 11:16 AM
54

55. Problems to Ponder
11/23/2011 11:16 AM
55

56. FREQUENCY CONVERSION AND
11/23/2011 11:16 AM
DEMODULATION
• Frequency Conversion
• Synchronous Detection
• Envelope Detection
56

57. Frequency Conversion
11/23/2011 11:16 AM
57

58. Synchronous Detection
11/23/2011 11:16 AM
58

59. Envelope Detection
11/23/2011 11:16 AM
59

60. Review Questions
11/23/2011 11:16 AM
60

61. Problems to Ponder
11/23/2011 11:16 AM
61