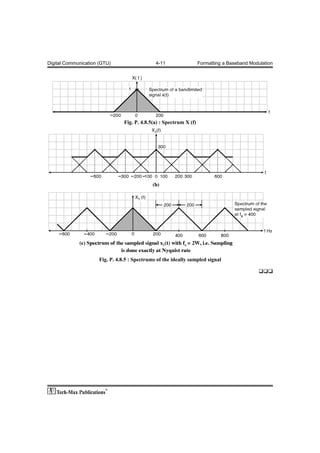
The document contains details about sampling a bandpass signal with varying center frequency fo from 5 kHz to 50 kHz at a sampling rate of 25 kHz. It analyzes the ranges of fo for which the sampling rate is adequate by calculating the variation in bandwidth (k) as fo changes. It concludes that the sampling rate of 25 kHz is adequate when fo is between 5-7.5 kHz, 15-20 kHz, 25-32.5 kHz, and 35-50 kHz.

1. Digital Communication (GTU) 4-1 Formatting a Baseband Modulation
Chapter 4 : Formatting a Baseband
Modulation
Section 4.6 :
Ex. 4.6.5 : A bandpass signal has a center frequency fo and extends from (fo – 5 kHz) to
(fo + 5kHz). This signal is sampled at a rate f s = 25 kHz. As the center frequency fo varies
from fo = 5 kHz to fo = 50 kHz, find the ranges of fo for which the sampling rate is
adequate. .Page No. 4-25.
Soln. : The bandpass signal is as shown in Fig. P. 4.6.5.
Fig. P. 4.6.5
We are going to use the general bandpass sampling theorem stated in Ex. 4.6.3.
From the data : f2 = fM = fo + 5 kHz
f1 = fo – 5 kHz
∴ Bandwidth B = f2 – f1 = 10 kHz.
Note that irrespective of the variation in “fo” the bandwidth B is going to remain constant.
However with changes in “fo” the highest frequency fM will change. This will force us to change the
values of “k” and hence the sampling rate “fs”.
In Table P. 4.6.5, we have covered the entire range of fo from 5 kHz to 50 kHz.
Table P. 4.6.5
Sr. Frequency Variation in fM Variation in k Variation in Comment
No. range of fo fM = (fo + 5 kHz) k = fM / B sampling frequency
fs = 2 fM / k
1. 5 to 7.5 kHz 10 to 12.5 kHz 1 to 1.25 i.e. 1 20 kHz to 25 kHz as fs ≤ 25 kHz
∴ Valid
2. 7.5 to 15 kHz 12.5 to 20 kHz 1.25 to 2 i.e. 1 25 kHz to 40 kHz fs > 25 kHz
∴ Invalid

2. Digital Communication (GTU) 4-2 Formatting a Baseband Modulation
Sr. Frequency Variation in fM Variation in k Variation in Comment
No. range of fo fM = (fo + 5 kHz) k = fM / B sampling frequency
fs = 2 fM / k
3. 15 to 20 kHz 20 to 25 kHz 2 to 2.5 i.e. 2 20 kHz to 25 kHz fs ≤ 25 kHz
∴ Valid
4. 20 to 25 kHz 25 to 30 kHz 2.5 to 3 i.e. 2 25 kHz to 30 kHz fs > 25 kHz
∴ Invalid
5. 25 to 32.5 kHz 30 to 37.5 kHz 3 to 3.75 i.e. 3 20 kHz to 25 kHz fs ≤ 25 kHz
∴ Valid
6. 32.5 to 35 kHz 37.5 to 40 kHz 3.75 to 4 i.e. 3 25 kHz to 26.66 kHz fs > 25 kHz
∴ Invalid
7. 35 to 45 kHz 40 to 50 kHz 4 to 5 i.e. 4 20 kHz to 25 kHz fs < 25 kHz
∴ Valid
8. 45 to 50 kHz 50 to 55 kHz 5 to 5.5 i.e. 5 20 kHz to 22 kHz fs < 25 kHz
∴ Valid
Conclusion :
From Table P. 4.6.5 it is evident that the sampling rate of 25 kHz is adequate for the following
frequency ranges of “fo” :
1. 5 to 7.5 kHz 2. 15 to 20 kHz
3. 25 to 32.5 kHz 4. 35 to 50 kHz.
Ex. 4.6.6 : The signals x1 (t) = 10 cos (100 πt) and x2 (t) = 10 cos (50 πt) are both sampled at times
tn = n / fs where n = 0, ± 1, ± 2, ... and the sampling frequency is 75 samples/sec. Show
that the two sequences of samples thus obtained are identical. What is this phenomenon
called ? .Page No. 4-25.
Soln. :
Let us prove that we get the identical sequences of samples by using the graphical method.
The signals x1 (t) and x2 (t) are cosine waves with equal peak amplitudes. Their frequencies are 50
Hz and 25 Hz respectively.
∴ x1 ( t ) : Has peak voltage = 10 V and f1 = 50 Hz
∴ x2 ( t ) : Has peak voltage = 10 V and f2 = 25 Hz
The sampling frequency fs = 75 Hz and sampling period Ts = 1/75 = 13.33 ms. Steps to be
followed to plot the sampled versions are as follows :
Step 1 : Draw the signals x1 ( t ), x2 ( t ) and the sampling function.
Step 2 : Encircle the sample values.
Step 3 : Draw the sampled signals x1 δ ( t ) and x2 δ ( t ).

3. Digital Communication (GTU) 4-3 Formatting a Baseband Modulation
All these waveforms are as shown in Fig. P. 4.6.6.
Fig. P. 4.6.6
Conclusion :
The sampling frequency of 75 Hz is lower than the Nyquist rate. Because to sample a 50 Hz
signal the sampling rate should atleast be 100 Hz. Therefore aliasing takes place. The identical sequence
in Fig. P. 4.6.6 are being obtained due to aliasing.
Section 4.7 :
Ex. 4.7.3 : A signal x (t) = cos 200 πt + 2 cos 320 πt is ideally sampled at fs = 300 Hz. If the sampled
signal is passed through an ideal low pass filter with a cutoff frequency of 250 Hz, what
frequency components will appear in the output? .Page No. 4-27.
Soln. : It has been given that x (t) = cos 200 πt + 2 cos 320 πt and fS = 300 Hz. The spectrum of the
ideally sampled signal is given by,
Xδ (f) = fs X (f – n fs) = 300 X (f – 300 n)
= 300 X (f) + 300 X (f ± 300) + 300 X (f ± 600) + … ...(1)
• The spectrum of x (t) is as shown in Fig. P. 4.7.3(a) which contains two frequency components
f1 = 100 Hz and f2 = 160 Hz.
• The second term in Equation (1) shows X (f) centered about ± fs = 300 Hz.

4. Digital Communication (GTU) 4-4 Formatting a Baseband Modulation
• The spectrum shifted towards right (see Fig. P. 4.7.3(b)) consists of four frequency components as
follows :
fs + f1 = 300 + 100 = 400 Hz
Fig. P. 4.7.3
Ex. 4.7.4 : Fig. P. 4.7.4(a) shows the spectrum of a low-pass signal g (t). The signal is sampled at
the rate of 1.5 Hz and then applied to a low-pass reconstruction filter with cut-off
frequency at 1 Hz.
1. Plot the spectrum of the sampled signal and specify distortion, if any.
2. If the low-pass reconstruction filter is to faithfully reproduce g (t) at its output, what
should be the minimum sampling frequency ? .Page No. 4-27.

5. Digital Communication (GTU) 4-5 Formatting a Baseband Modulation
Fig. P. 4.7.4(a)
Soln. : Given : Sampling frequency fs = 1.5 Hz
Cut-off frequency of a low pass filter fcut – off = 1 Hz.
1. Spectrum of the sampled signal :
The spectrum of sampled signal is given by,
Gδ (f) = fs G (f – nfs)
The spectrum of the sampled signal is as shown in Fig. P. 4.7.4(b).
As shown in Fig. P. 4.7.4(b) the spectrums overlap giving rise to a distortion called “Aliasing”.
2. If a low pass filter is to faithfully reproduce g (t) then the minimum sampling rate should be
fs (min) = 2 × 1 = 2 Hz ...Ans.
Fig. P. 4.7.4(b) : Spectrum of the sampled signal
Ex. 4.7.5 : A signal g(t) contains two frequencies 1000 Hz and 5000 Hz expressed as
g (t) = (cos 6280 t + cos 31400 t). It is sampled at 8000 samples/sec. Determine the
spectrum of sampled signal and plot the spectrum. Assume instantaneous sampling. This
sampled signal is passed through a LPF with constant unity gain from 0 to 2 kHz and

6. Digital Communication (GTU) 4-6 Formatting a Baseband Modulation
linearly decreasing gain from 2 kHz to 4 kHz with a zero gain at 4 kHz. Determine the
output and interpret the result. .Page No. 4-27.
Soln. :
Step 1 : Plot the spectrum of g (t) :
g (t) = cos 6280 t + cos 31400 t
∴ g (t) = cos (2 π × 1000 t) + cos (2 π × 5000 t) ...(1)
• To plot the spectrum of g (t), we need to obtain its fourier transform. The fourier transform of a
cosine wave is as,
cos (2 π fo t) δ (f – fo) + δ (f + fo) ...(2)
• Applying this to signal g (t) we get the spectrum of g (t) as :
G (f) = + ...(3)
• This spectrum is plotted in Fig. P. 4.7.5(a).
Fig. P. 4.7.5
Step 2 : Spectrum of instantaneously sampled signal :
• We know that the spectrum of ideally sampled signal is given by,

7. Digital Communication (GTU) 4-7 Formatting a Baseband Modulation
Gδ (f) = fs (f – n fs) ...(4)
But fs = 8000
∴ Gδ (f) = 8000 G (f – 9000 n)
• Expanding this expression we get,
Gδ (f) = 8000 G (f) + 8000 G (f – 8000) + 8000 G (f + 8000) + … ...(5)
• Equation (5) has the following terms :
1. First term : 8000 G (f) : Spectrum of g (t)
2. Second term : 8000 G (f – 8000) : Spectrum of g (t) shifted by 8000 Hz.
3. Third term : 8000 G (f + 8000) : Spectrum of g (t) shifted by 8000 Hz. There are infinite
number of such terms. The spectrum Gδ (f) is shown in Fig. P. 4.7.5(b).
Step 3 : Frequency response of filter :
The frequency response of the LPF is plotted in Fig. P. 4.7.5(c).
Output : The output is as shown in Fig. P. 4.7.5(d).
Section 4.8 :
Ex. 4.8.3 : The spectrum of a signal g (t) is shown in Fig. P. 4.8.3. This signal is sampled with a
periodic train of rectangular pulses of duration 50/3 milliseconds. Plot the spectrum of the
sampled signal for frequencies up to 50 Hz for the following two conditions :-
1. The sampling rate is equal to the Nyquist rate.
2. The sampling rate is equal to 10 samples per second. .Page No. 4-44.
Fig. P. 4.8.3

8. Digital Communication (GTU) 4-8 Formatting a Baseband Modulation
Soln. :
Spectrum when fs = Nyquist rate :
1. It has been given that the width of the sampling pulse is τ = = 16.66 ms. Therefore this is the
“natural sampling” of the signal. The spectrum of naturally sampled signal is given by,
S (f) = sinc (n fs τ) × (f – n fs) ...(1)
2. Here τ = 16.66 ms, fs = 20 Hz if fs = Nyquist rate.
The sinc function goes to 0 when (n fs τ) = ± 1, ± 2 …
That means when f = n fs = ± , ± ...
i.e. when f = ± , ± ...
i.e. when f = ± 61.23 Hz, ± 122.5 Hz....
The spectrum of the sampled signal at Nyquist rate is as shown in Fig. P. 4.8.3(a).
Fig. P. 4.8.3(a) : Spectrum for fs = Nyquist rate
Note that the amplitude is = τ A fs = 16.33 × 10– 3 × 20
= 0.3266 (Assuming A = 1)

9. Digital Communication (GTU) 4-9 Formatting a Baseband Modulation
Spectrum for fs = 10 Hz :
The shape of the spectrum remains same. But due to the reduced value of f s the spectrums
overlap as shown in Fig. P. 4.8.3(b).
Fig. P. 4.8.3(b) : Spectrum for fs = 10 Hz
Ex. 4.8.4 : A waveform g (t) = 20 + 20 sin (500 t + 30°), is to be sampled periodically and reproduced
from these sample values –
1. Find the maximum allowable time interval between sample values.
2. How many sample values need to be stored in order to reproduce 1 sec. of this
waveform if sampled according to the results in 1.
3. Determine and sketch the spectrum of the sampled signal when sampling frequency
fs = 750 Hz. .Page No. 4-44.
Soln. :
1. The input waveform is x (t) = 20 + 20 sin (500 t + 30°). The first term represents a dc shift
whereas the second term is a sinewave of frequency fm = 500/2 π = 79.58 Hz.
2. Therefore the minimum sampling rate is given by,
fs (min) = 2 fm = 2 × 79.58 = 159.16 Hz.
3. The maximum allowable time interval between the sample values is given by,
Ts (max) = =
∴ Ts (max) = 6.28 msec ...Ans.
4. The number of samples needed to be stored to produce 1 sec is given by,
Number of samples = 1 sec. / 6.28 msec. = 159.16 samples ...Ans.
Spectrum of the sampled signal :
Given : fs = 750 Hz
1. The spectrum of the input signal g (t) is as shown in Fig. P. 4.8.4(a). The maximum signal
frequency is W = 159.16 Hz. and the DC component at f = 0 has an amplitude of 20V.

10. Digital Communication (GTU) 4-10 Formatting a Baseband Modulation
Fig. P. 4.8.4(a) : Spectrum of input signal
2. The spectrum of the sampled signal is given by,
Gδ (f) = fs G (f – n fs)
It is as shown in Fig. P. 4.8.4(b)
Fig. P. 4.8.4(b) : Spectrum of the sampled signal
Ex. 4.8.5 : A low pass signal x (t) has a spectrum X (f) given by
X (f) =
1. Assume that x (t) is ideally sampled at f s = 300 Hz. Sketch the spectrum of the
sampled x (t) for | f | < 600.
2. Repeat part 1. with fs = 400 Hz. .Page No. 4-44.
Soln. :
From the given expression of X (f), its shape is as shown in Fig. P. 4.8.5(a). Note that at f = 0,
X (f) = 1 – 0 = 1 and at f = 200 X (f) = 1 – 1 = 0.
1. The spectrum of an ideally sampled signal with fs = 300 Hz is as shown in Fig. P. 4.8.5(b). Note
that the spectrum X (f) gets repeated at ± fs, ± 2 fs,… As fs is less than 2 fs i.e. Nyquist rate the
overlapping of spectrums takes place.
2. The spectrum of ideally sampled signal with fs = 400 Hz i.e. exact Nyquist rate is as shown in
Fig. P. 4.8.5(c). Note that the adjacent spectrums touch each other.

11. Digital Communication (GTU) 4-11 Formatting a Baseband Modulation
Fig. P. 4.8.5(a) : Spectrum X (f)
Fig. P. 4.8.5 : Spectrums of the ideally sampled signal
