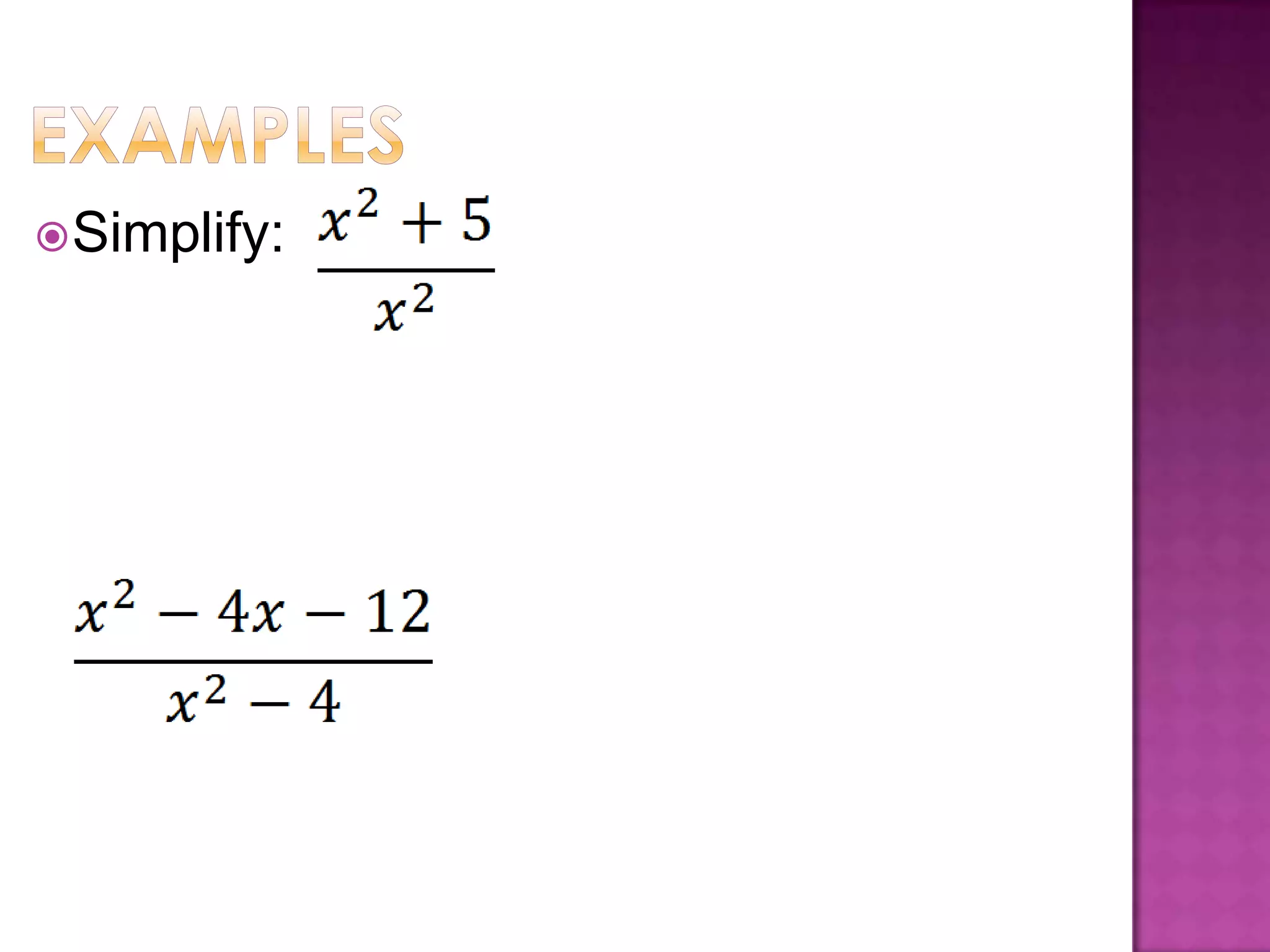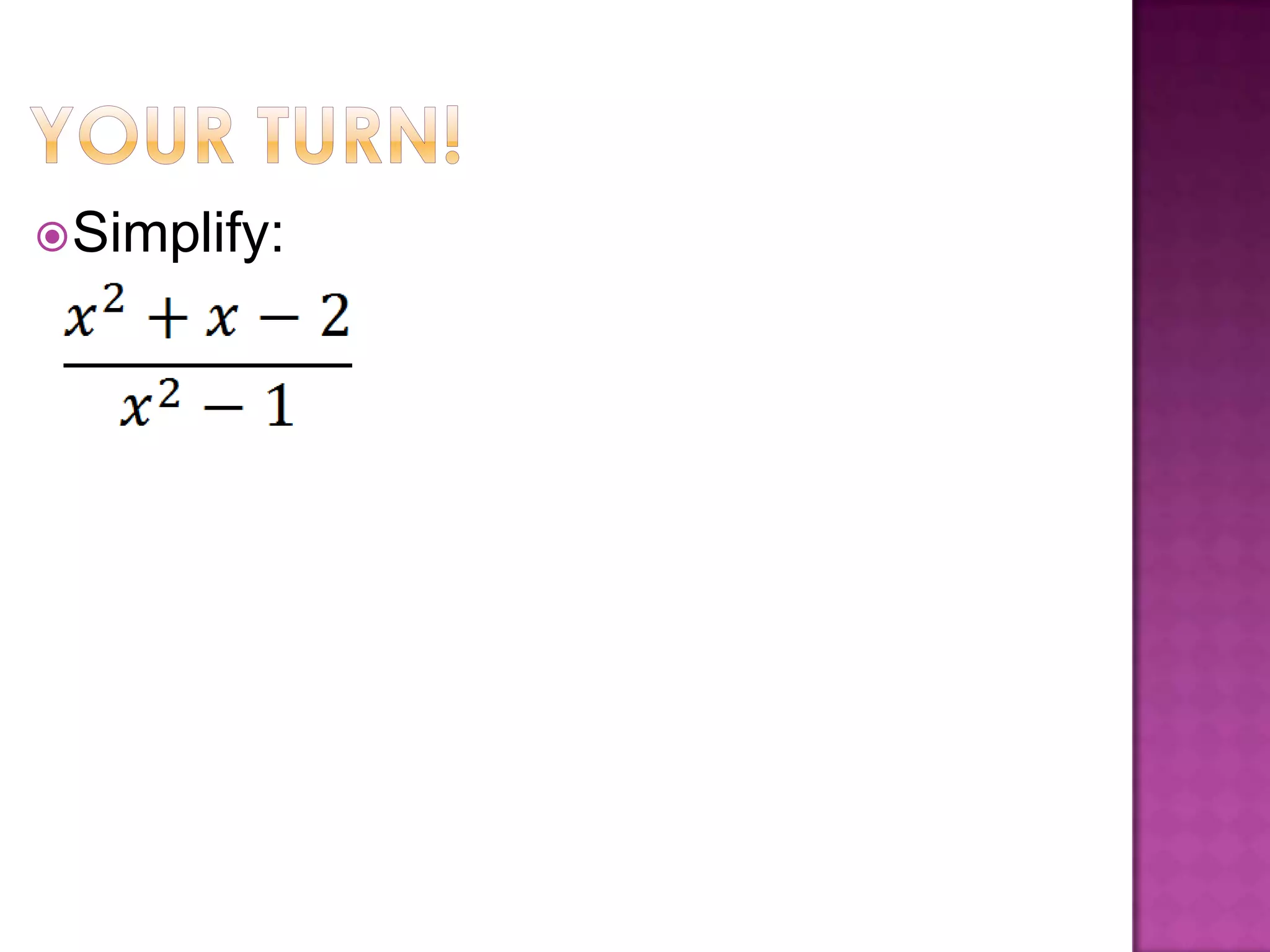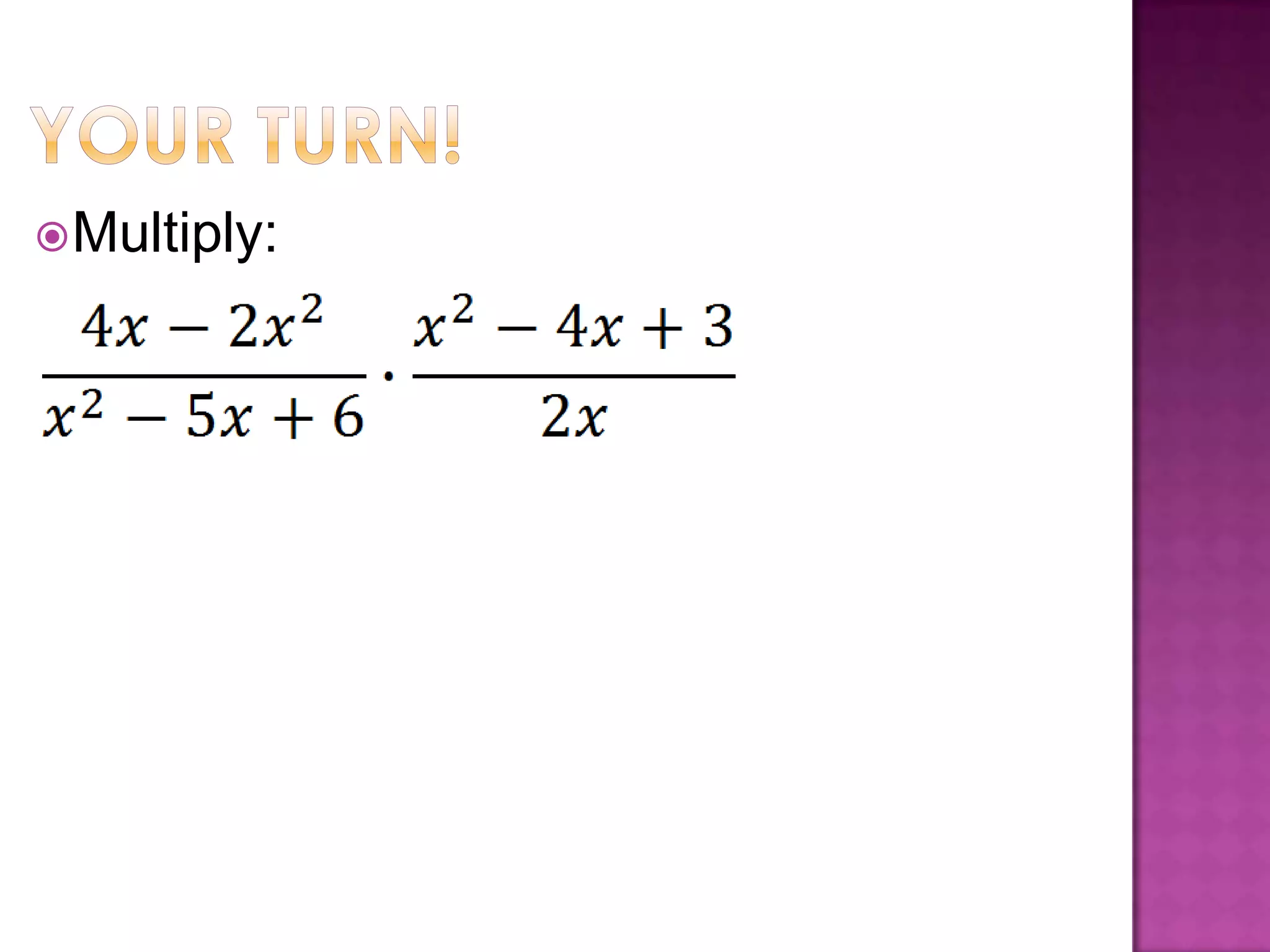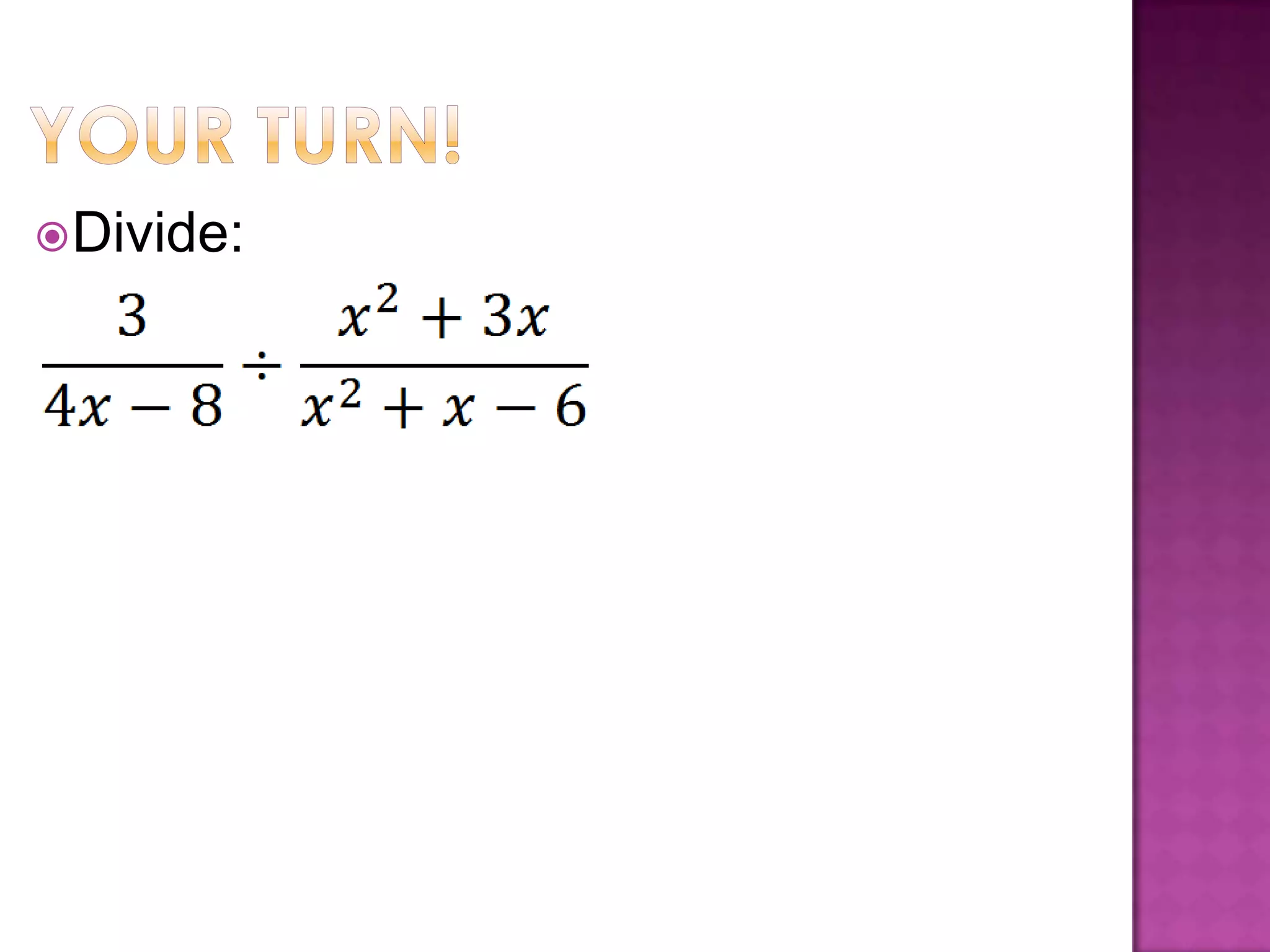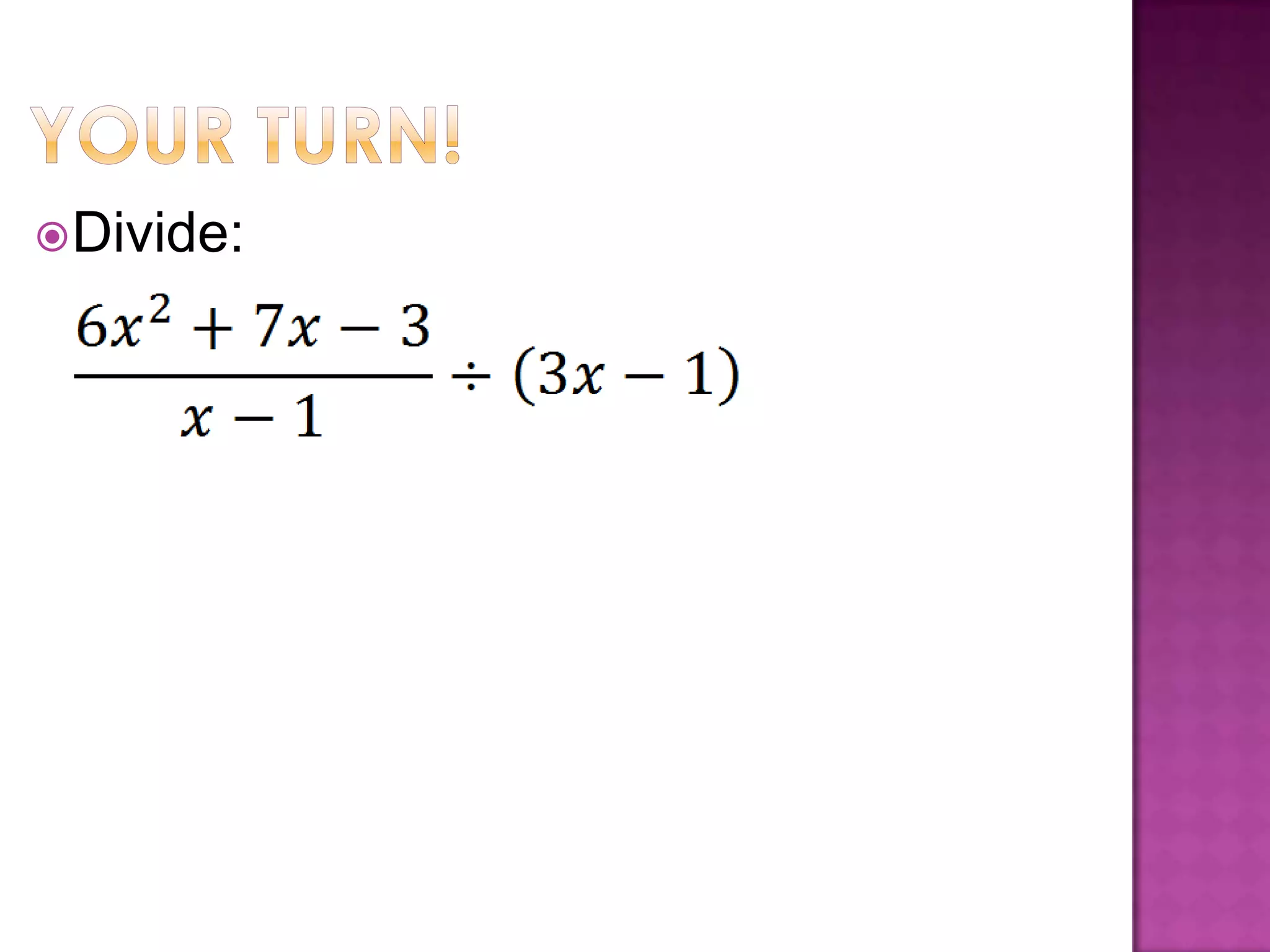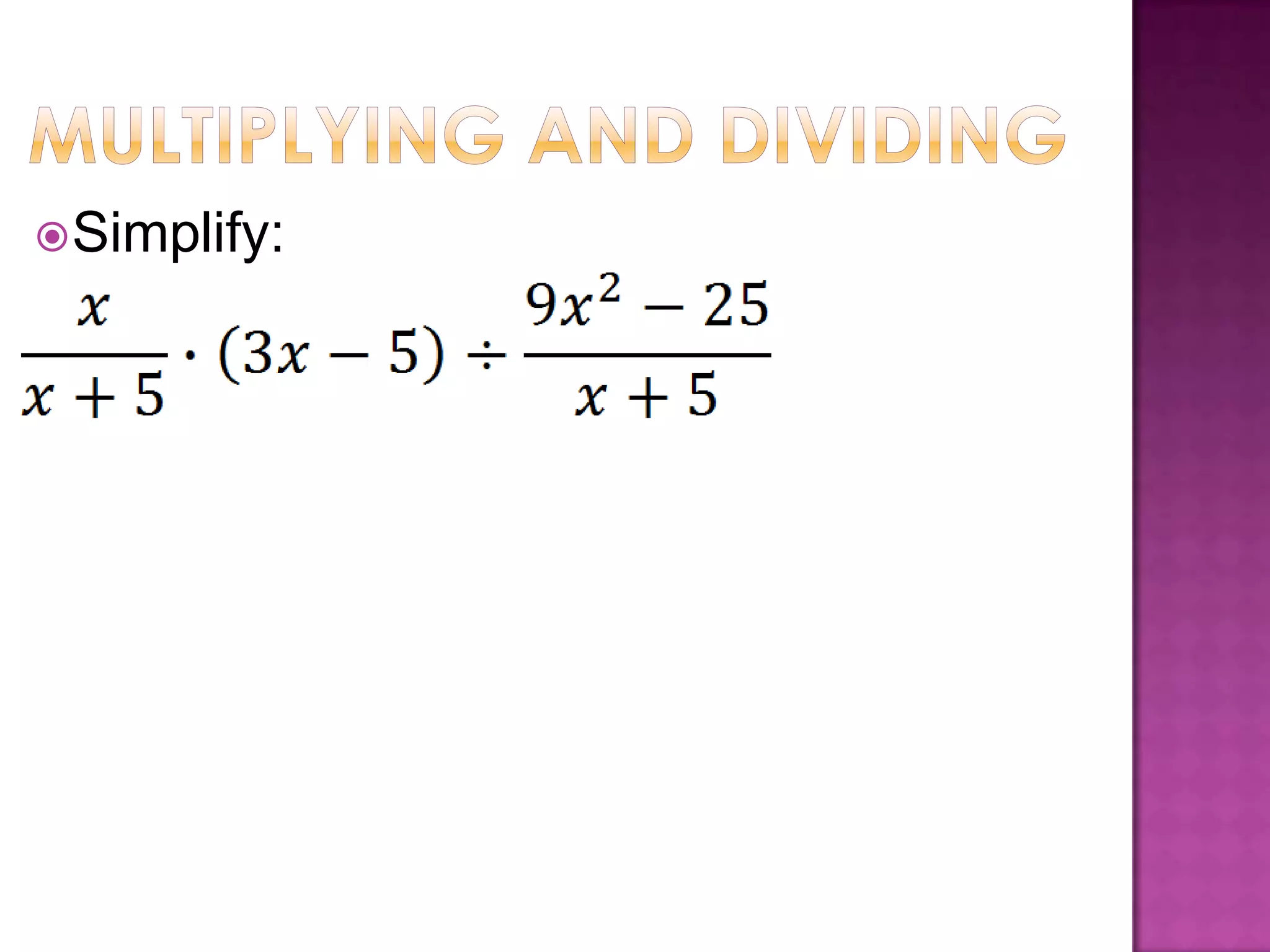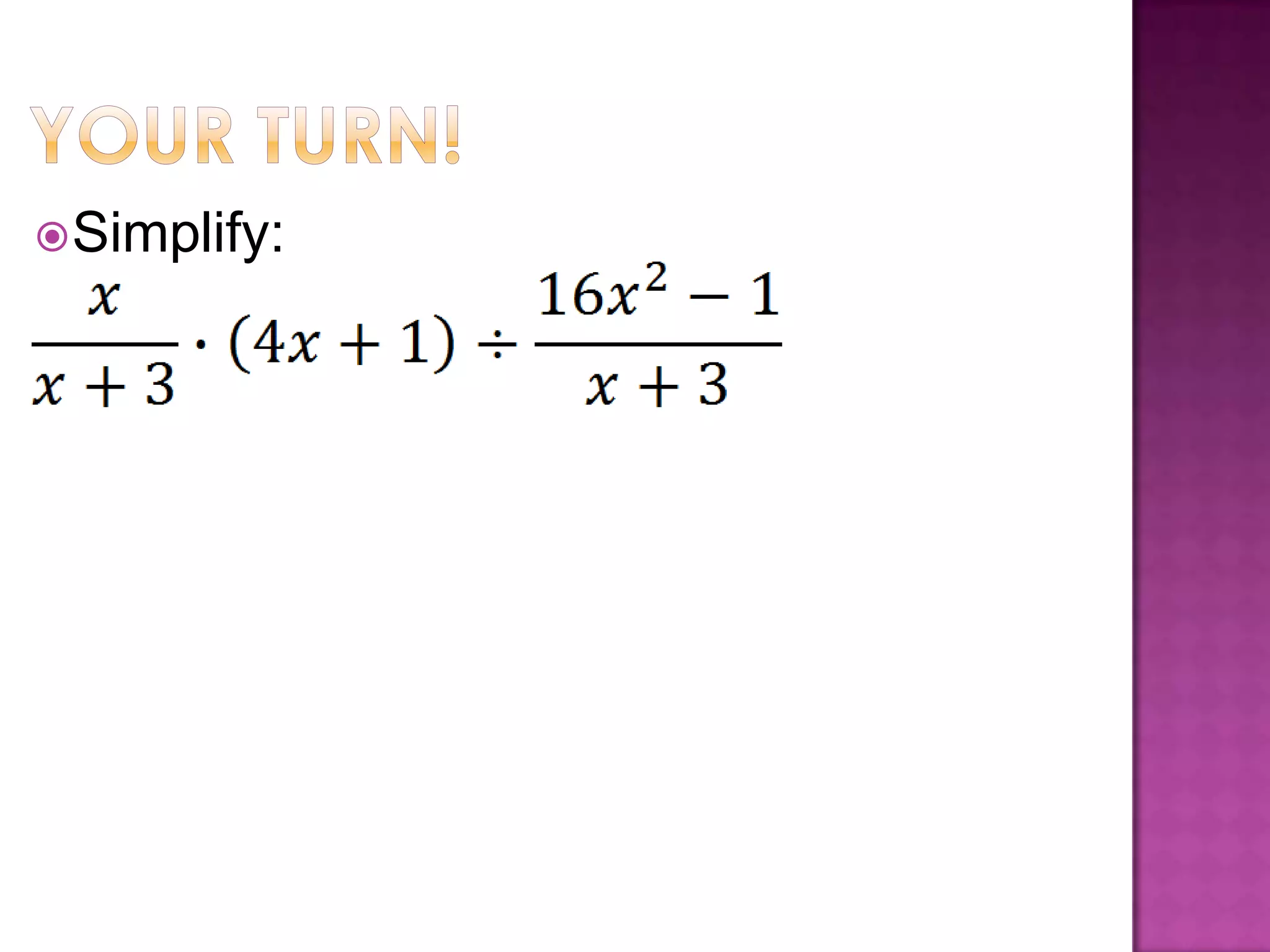Embed presentation
Downloaded 88 times


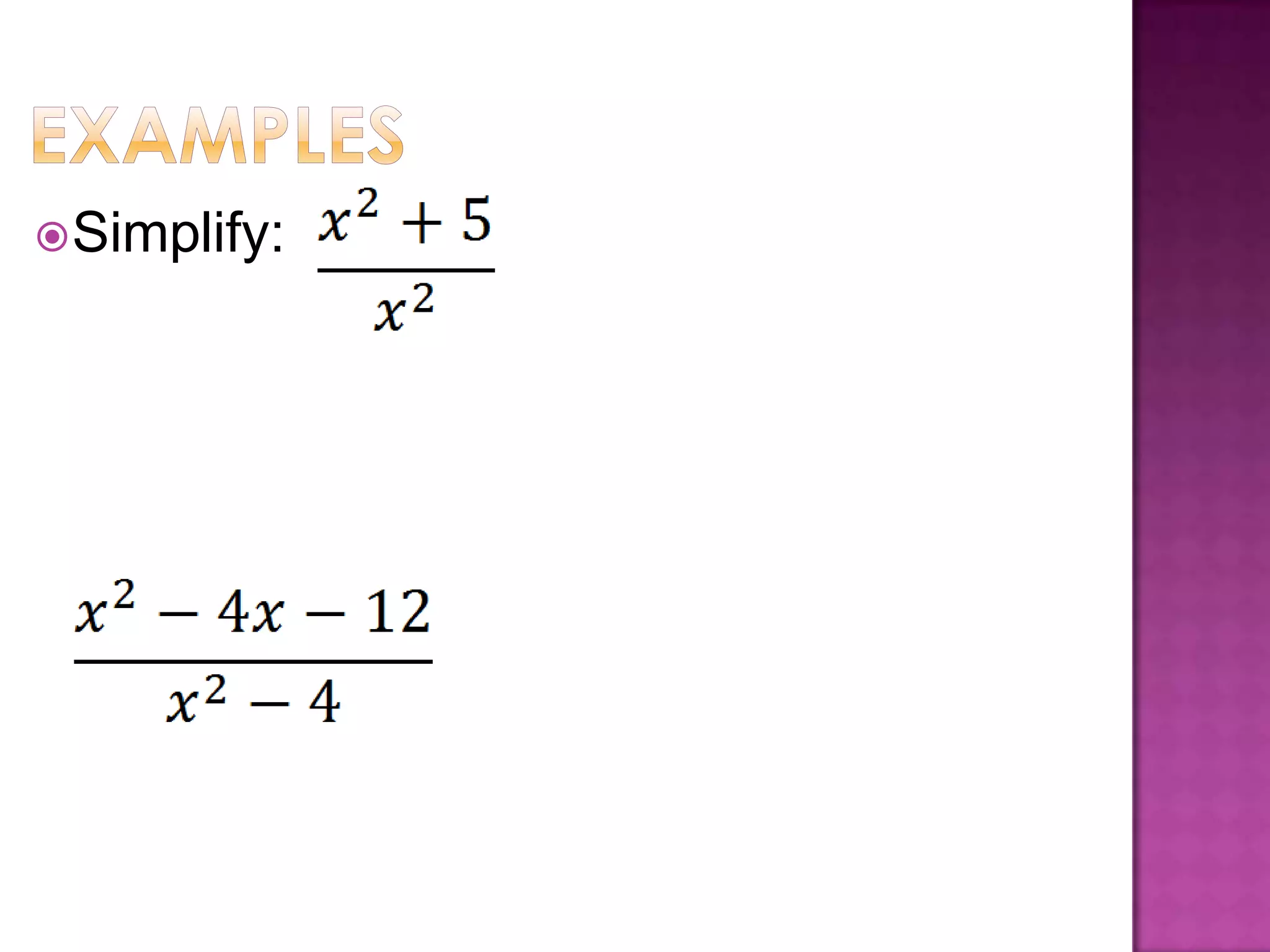
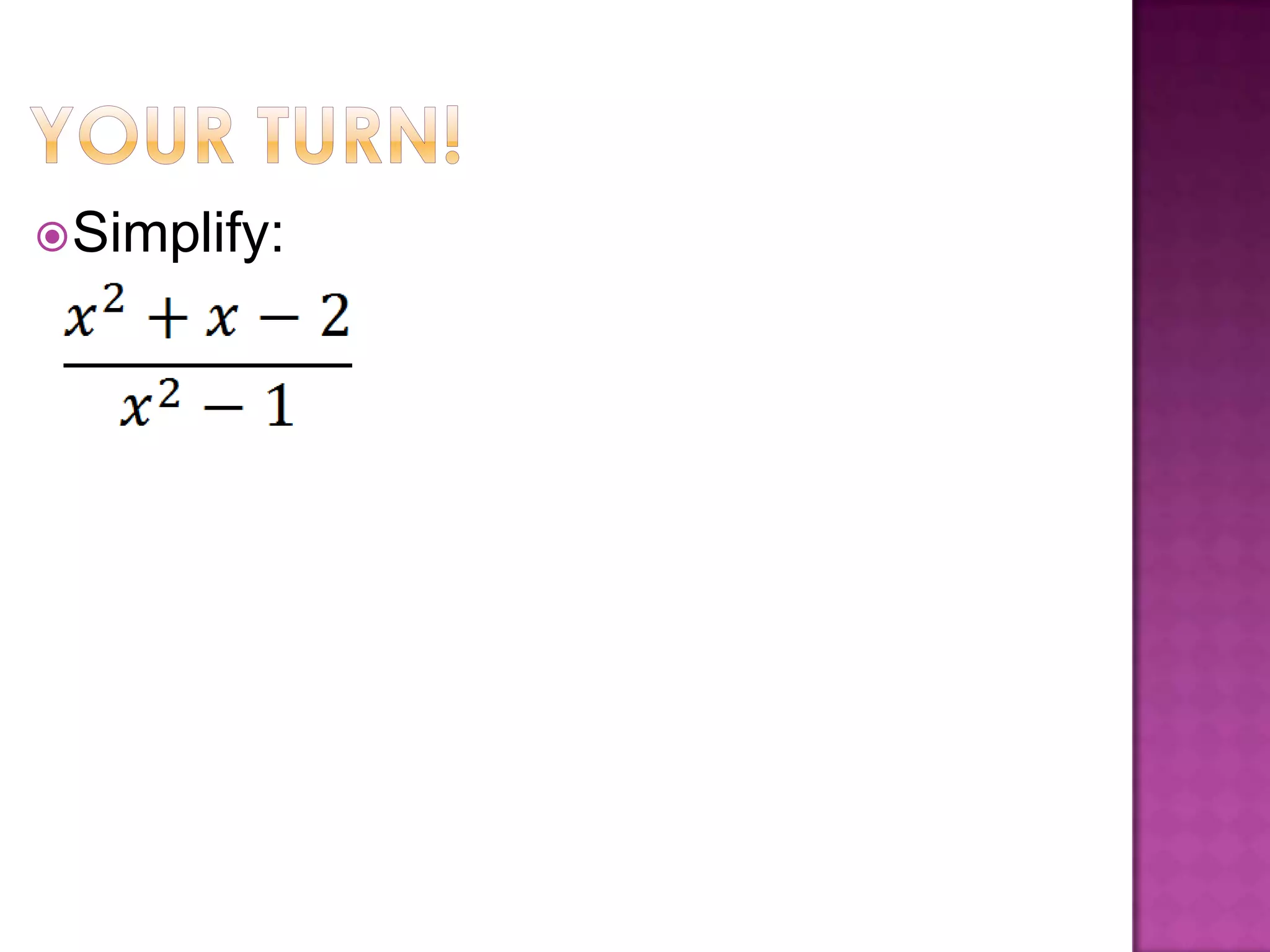



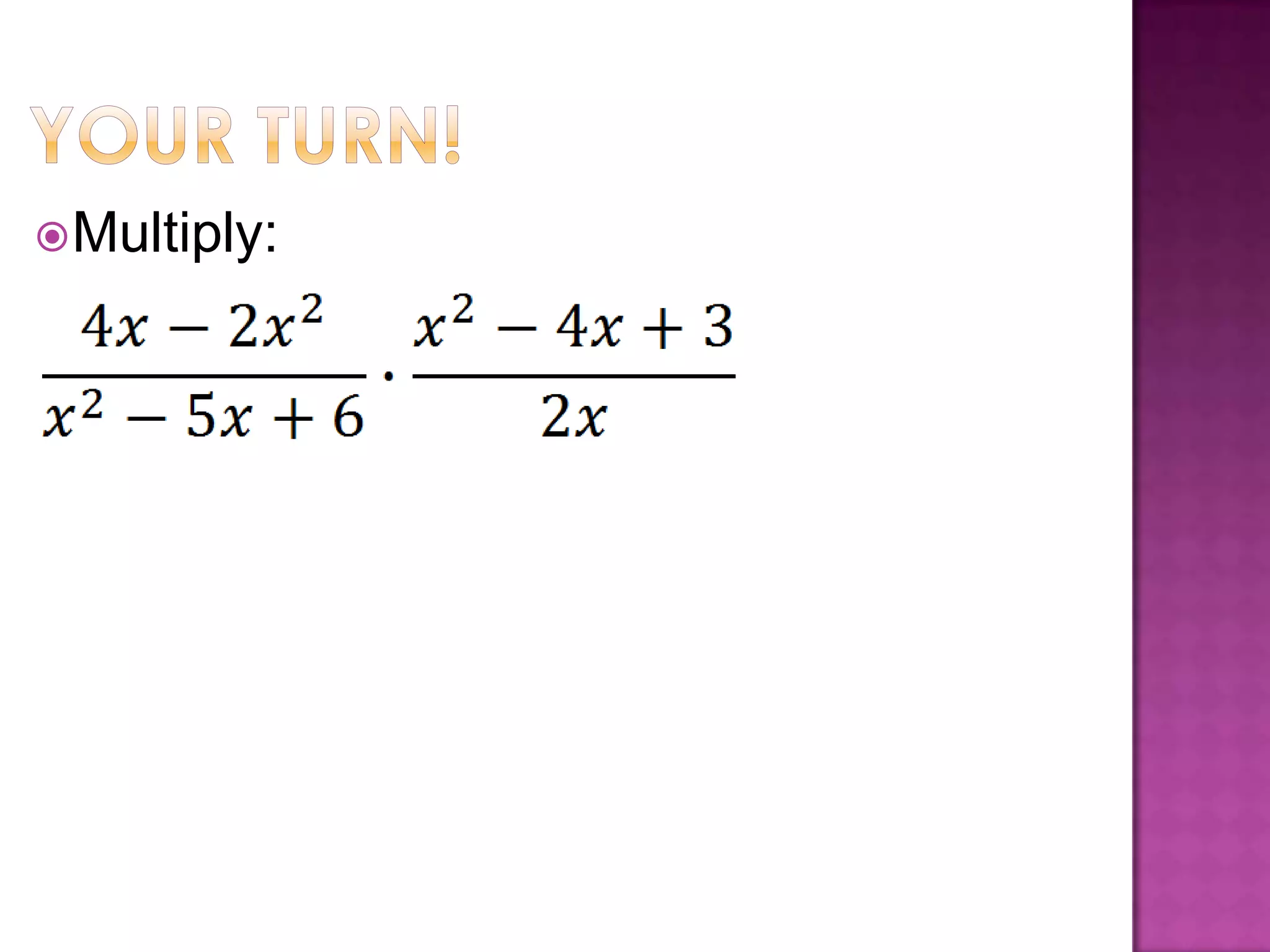



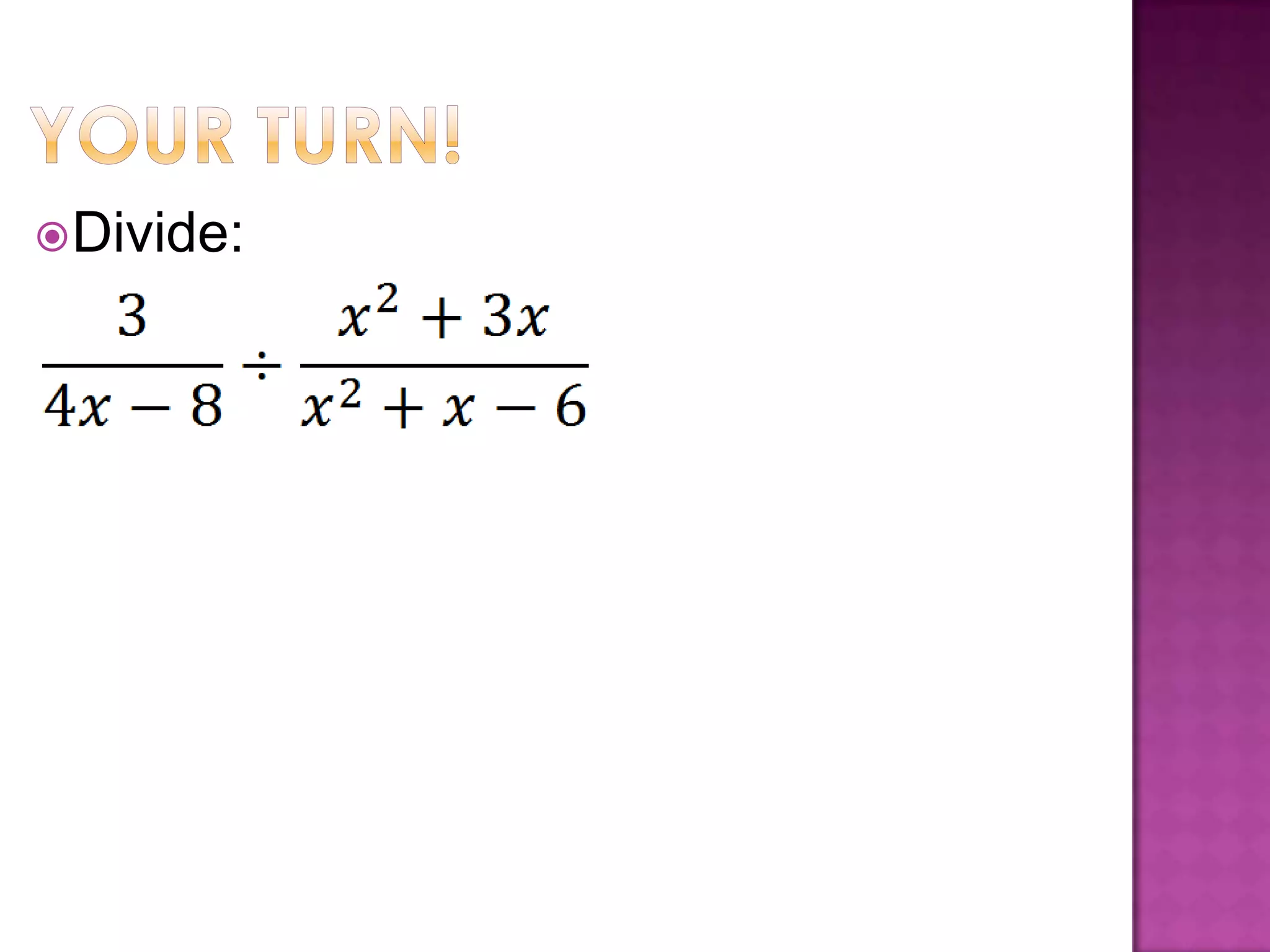

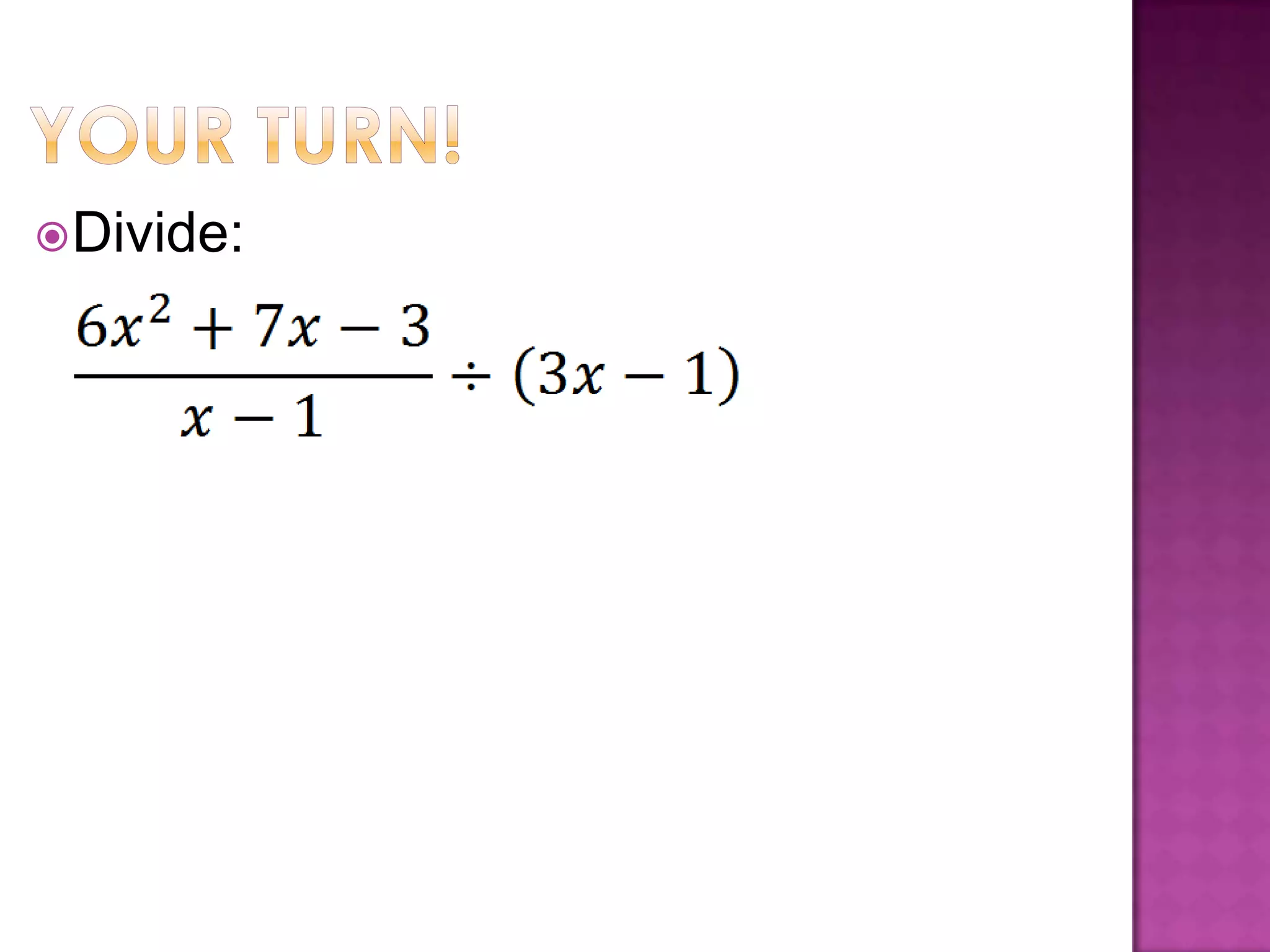
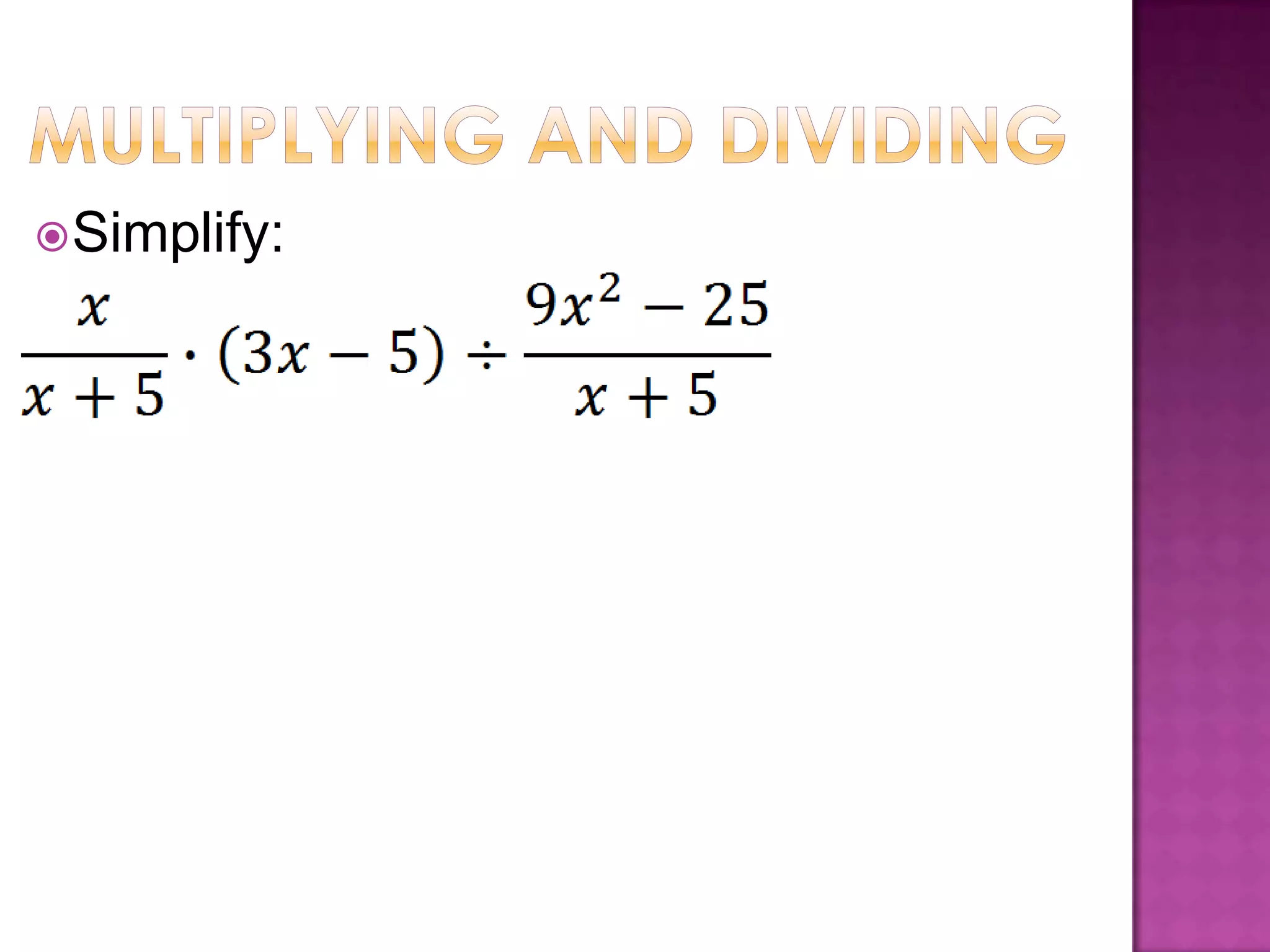
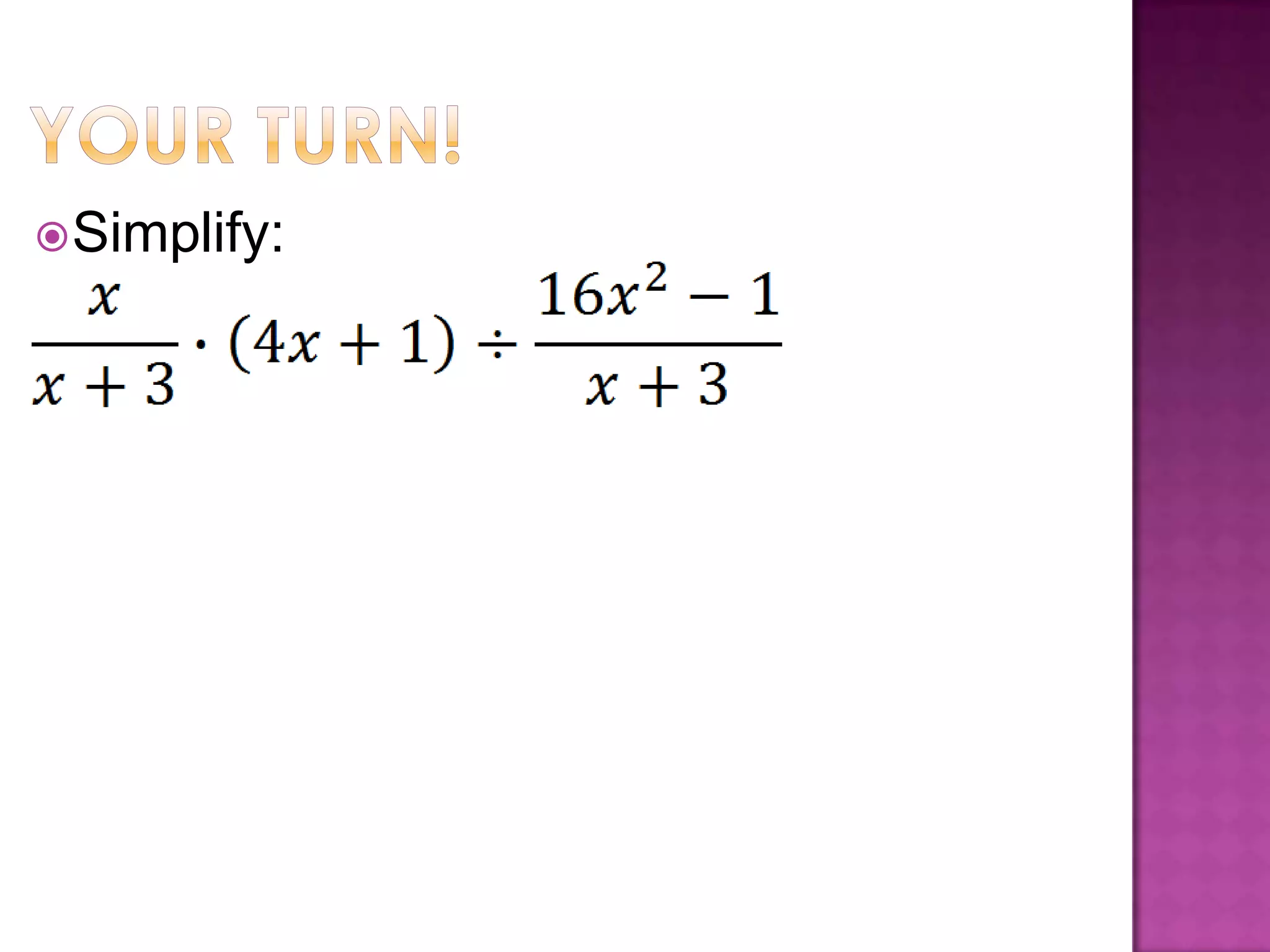
A rational expression is in simplified form when the numerator and denominator have no common factors other than 1. To simplify a rational expression, factor the numerator and denominator and cancel any common factors; this works the same as multiplying fractions by multiplying numerators and denominators and then simplifying. Examples are provided for multiplying and dividing rational expressions by factoring, multiplying or dividing numerators and denominators, and then simplifying.