This document provides examples of calculations related to rigid pavement design, including: 1) Calculating the spacing between contraction joints for plain and reinforced concrete slabs of varying thickness and reinforcement. 2) Computing the radius of relative stiffness for concrete slabs over subgrade, given slab properties and subgrade modulus. 3) Determining wheel load stresses, dowel bar sizing and spacing, equivalent resisting section radius, and contraction joint tensile stress. 4) Summarizing the process for designing a rigid pavement using Westergaard wheel load and wrapping stress equations at the slab edge.

1. • Example: Find the spacing between contraction joints for 3.8m slab width having thickness of 20 cm and
f=1.5, for the following cases:
• (1) Plain cement concrete (11) for reinforced cement concrete with 1cm dia bars at 32cm spacing.
• (i) For plain cement concrete slab:
• Assume unit weight of concrete (W)= 2400kg/m3 Allowable tensile stress in concrete = 0.8 Kg/cm2.
• Spacing between contraction joints= 2xSc x104/W. f = 2x0.8x104/2400x1.5 = 4.44m or 4.5m.
• (ii) For reinforced cement concrete slab:
• Spacing between contraction joints: Lc = 200x SsxAs / bhwf
• Here As = Area of steel in 3.8 m width of the slab in 32cm spacing = 3.14x 1x1 x 3.8 x 100/4 x32 = 9.32 cm2
• So, spacing of contraction joint = 200 x1750 x 9.32 / 3.8 x 20 x 2400 x 1.5 = 11.9 m
• (Here Ss= allowable tensile strength of the steel is assumed as 1750 kg/cm2), and over
• Example: Find radius of relative stiffness for a 20cm slab with E= 3x105 kg/cm2 and Poisson’s ratio =0.15, over
subgrade of modulus 5kg/cm3.
• E= 3x105 kg/cm2 , 𝜇 = 0.15, ℎ = 20𝑐𝑚 𝑎𝑛𝑑 𝑘 = 5kg/cm3.
• Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 3𝑥105
𝑥203
12𝑥5 ( 1−0.152)
= 79.98 cm.

2. • Example: Compute radius of relative stiffness for a 15cm slab with E= 2.1x105 kg/cm2 and
Poisson’s ratio =0.15, over subgrade of modulus (a) k= 3.5kg/cm2 (b) k= 7kg/cm2 .
• E= 2.1x105 kg/cm2 , 𝜇 = 0.15, ℎ = 15𝑐𝑚 𝑎𝑛𝑑 𝑘 = 3.5kg/cm2.
• Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 2.1𝑥105𝑥153
12𝑥3.5 ( 1−0.152
)
= 64.46 cm
• For k= 7.0 kg/ cm2.
• Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 2.1𝑥105𝑥153
12𝑥7.0 ( 1−0.152
)
= 54.2 cm.
• Example: Compute the equivalent radius of resisting section of 20cm thick slab, given
that the radius of contact area wheel load is 16cm.
• Slab thickness h= 20cm. Radius of wheel load distribution, a =16cm. So a/h= 16/20 = 0.80
< 1.724
• Therefore equivalent radius of the resisting section when ( a< 1.724 h)
• b = 1.6𝑎2 + ℎ2 - 0.675h = 1.6 𝑋 162 + 202 - (0.675x20) = 14.95cm.

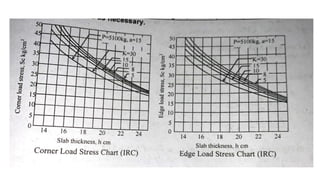
3. • Example: Using data given below determine:
• (a) Edge and Corner load stresses by Westergaard equation.
• Wheel load P= 5200kg, pavement thickness h= 18cm, Poisson ratio of concrete 𝜇 = 0.15,
radius of contact area ‘a’ = 15cm, Modulus of elasticity of concrete= E= 3.0x105 kg/cm2 ,
modulus of subgrade reaction k= 6.0 kg/cm2
• Solution: Radius of relative stiffness; l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 3.0𝑥105𝑥183
12𝑥6.0 ( 1−0.152
)
= 70.6 cm.
• Equivalent radius of resisting section is given by a/h = 15/18 = 0.833 <1.724
• Therefore equivalent radius of the resisting section= b = 1.6𝑎2 + ℎ2 - 0.675h =
1.6 𝑋 152 + 182 - (0.675x18) = 14cm.
• Edge load stress, σe =
0.572 𝑃
ℎ2 {4 log10 (l/b) +0.359 } =
0.572 𝑥 5200
182 {4 log10 (70.6/14) +0.359}
= 29.1 kg/ cm2
• Corner load Stress σc =
3𝑃
ℎ2 [ 1- (
𝑎√2
𝑙
) 0.6 =
3𝑥5200
182 [ 1- (
15√2
70.6
) 0.6 ] = 24.75 kg/ cm2

4. • Example: The spacing between the contraction joint of a CC pavement is 4.25m.
Determine the tensile stress developed in the CC pavement due to contraction if the
coefficient of friction between the bottom of the pavement and the supporting layer is
1.1 and unit weight of concrete 2400 kg/m3.
• Solution: Equating the total force( in Kg) developed in the cross section of the concrete
pavement due to movement half of the length of slab ( Lc/2) and the frictional
resistance due to the restraint at the interface in half of the slab length,
• Sf x h x b x 100 (kg) = b x ( Lc/2) x h/100 x w x f (kg) 𝑆𝑓 = W Lc f/ 2x104
• Where Sf = stress developed due to interface friction in cement concrete pavement
/unit area. W= unit weight of concrete =2400 kg/m3
• f= coefficient of friction at interface (maxm. value =1.5)
• Lc = Spacing between contraction joint = slab length (m), b = slab width (m).
• Given L = 4.25m. f =1.1, W = 2400 kg/m3
• Tensile stress developed in the pavement due to contraction Sf = W Lc f/ 2x104 =
• 2400 x 4.25 x 1.1/ 2 x 10 4 = 0.561 kg/cm2.

5. Example: Design size and spacing of dowel bars at an expansion joint of concrete pavement of thickness 20
cm. Given the radius of relative stiffness of 90 cm. design wheel load 4000 kg. Load capacity of the dowel
system is 40 percent of design wheel load. Joint width is 3.0 cm and the permissible stress in shear, bending
and bearing stress in dowel bars are 1000,1500 and 100 kg/cm2 respectively.
• Given, P = 4000 kg, l = 90 cm, h = 20 cm, δ = 3 cm, Fs = 1000 kg/cm2, Ff = 1500 kg/cm2 and Fb = 100 kg/cm2;
and assume d = 2.5 cm diameter.
• Step-1: length of the dowel bar Ld,
• Ld = 5×2.5 1500 𝐿𝑑 + 1.5 × 3 / {100 (Ld +8.8×3)} = 12.5× 15
𝐿𝑑+4.5
(𝐿𝑑 + 26.4)
/
• Solving for Ld by trial and error, it is =39.5cm Minimum length of the dowel bar is Ld + δ = 39.5 + 3.0 = 42.5
cm, So, provide 45cm long and2.5cm φ. Therefore Ld =45−3=42cm.
• Step 2: Find the load transfer capacity of single dowel bar
• Ps = 0.785 × 2.52 × 1000 = 4906.25 kg, Pf = 2×2.53×1500 / 42.0+8.8×3 = 685.307 kg, Pb = 100×2.5×42.02/ 12.5
(42.0+1.5×3) = 758.71 kg
• Therefore, the required load transfer capacity (refer equation)
• max {0.4×4000/ 4906.25, 0.4×4000/ 685.307, 0.4×4000/ 758.71} = max {0.326, 2.335, 2.10} = 2.335
• Step-3 : Find the required spacing: Effective distance of load transfer = 1.8 × l = 1.8 × 90 = 162 cm.
• Assuming 35 cm spacing, Actual capacity is 1+
162−35
162
+
162−70
162
+
162−105
162
+
162−140
162
= 2.83
• Assuming 40 cm spacing, Actual capacity is 1+
162−40
162
+
162−80
162
+
162−120
162
+
162−160
162
= 2.52
• So we should consider 2.52;2.335 as it is greater and more near to other value. Therefore provide 2.5 cm φ
mild steel dowel bars of length 45 cm @ 40 cm center to center.

6. • Example: Using data given below, calculate wheel load stresses at:- ( a) Interior (b) Edge ( c) Corner regions of a
cement concrete pavement using westargaard stress equation and also determine the probable location of crack is
likely to develop due to corner loading. Wheel load =5200Kg. E= 3.0x105 kg/cm2 , 𝜇 = 0.15, ℎ = 18𝑐𝑚 𝑎𝑛𝑑 𝑘 =
6.0kg/cm3 Radius of contact area= 15cm.
• Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 3𝑥105𝑥183
12𝑥6 ( 1−0.152
)
= 70.6 cm.
• Equivalent radius of the resisting section= b = 1.6𝑎2 + ℎ2 - 0.675h = 1.6 𝑋 152 + 182 - (0.675x18) = 14cm.
• ( a/h = 15/18 = 0.833 < 1.74)
• Interior load stress, σi =
0.316 𝑃
ℎ2 {4 log10 (l/b) +1.069 } =
0.316 𝑥 5200
182 {4 log10 (70.6/14) +1.069 }= 19.68kg/cm2 .
• Edge load stress, σe =
0.572 𝑃
ℎ2 {4 log10 (l/b) +0.359 } =
0.572 𝑥 5200
182 {4 log10 (70.6/14) +0.359} = 29.1 kg/ cm2
• Corner load Stress σc =
3𝑃
ℎ2 [ 1- (
𝑎√2
𝑙
) 0.6 =
3𝑥5200
182 [ 1- (
15√2
70.6
)] 0.6 = 24.75 kg/ cm2
• Location where corner load cracks develop: location where the crack is likely to develop due to corner loading,
the distance from the corner of the slab, x = 2.58 (a.l)1/2 = 2.58x( 15x 70.6) ½ = 83.96 cm = 84 cm.
• Example: Determine the wrapping streses at interior, edge and corner of 30cm thick cement concrete pavement
with transverse joint at 5m interval and longitudinal joints at 3.6 m interval. The modulus of subgrade reaction =
𝑘 = 6.9kg/cm3 and radius of loaded area is 15 cm. Assume maximum temperature differential during day to be 0.6
0C per cm slab thickness ( for wrapping stresses at interior and edge) and maximum temperature differential at 0.4
0C per cm slab thickness during night ( for wrapping stress at corner). Other data are E= 3.0x105 kg/cm2 , 𝜇 =
0.15, ∝ = 10𝑥10-6 per 0C.

7. • Given Slab thickness h= 30cm. Modulus of Elasticity E= 3.0x105 kg/cm2 , Poission’s ratio =𝜇 = 0.15,
Thermal coefficient of temperature ∝ = 10𝑥10-6 per 0C. a= 15 cm. Lx= 500 cm, Ly =360 cm.
• Temperature differential during day, t1 = 0.6x 30 = 180C
• Temperature differential during night, t2 = 0.4x 30 = 120C
• Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 3𝑥105𝑥303
12𝑥6.9 ( 1−0.152)
= 100 cm.
• Lx /l= 500/100 = 5 , Ly / l =360/100 =3.6 , Refer to Bradbury’s Chart for wrapping stress coefficients
corresponding to Lx /l = 5 , Cx =0.75, Ly /l = 3.6 , Cy =0.4,
• Wrapping stress at interior region of the slab, during day
Sti =
E ∝ t
2
[
Cx +𝜇 Cy
1−𝜇2 ] =
3𝑥 105𝑥 10 𝑥10
−
6
𝑥18
2
[ 0.75 + 0.15x 0.4/ (1- 0.152 )= 22.4 kg/cm2
Wrapping stress at edge region of the slab, during day
Ste =
Cx E ∝ t
2
[ as it is higher than
Cy E ∝ t
2
] =
0.75𝑥 3𝑥 105𝑥 10 𝑥10
−
6
𝑥18
2
= 20.25kg/cm2
Wrapping stress at corner region of the slab, during night,
Stc =
E ∝ t
3 ( 1−𝜇 )
( a/l) ½ =
3𝑥 105𝑥 10 𝑥10
−
6
𝑥12
3 ( 1−0.15)
( 15/ 100) 1/2 = 5.47 kg/cm2

8. • Example: Design a rigid pavement making use of wastergaard wheel load and wrapping stress equations at
the edge region of the slab. The design data are given below:
• Design wheel load P= 7500Kg, Contact pressure p= 7.5Kg/cm2, spacing between longitudinal joints= 3.75 m
, spacing between contraction joint= 4.2m. E= 3.0x105 kg/cm2 Poisson′
s ratio, 𝜇 = 0.15, Thermal
coefficient of cc 0C ∝ = 1𝑥10-5. Flexural strength of cc = 45 kg/cm2 modulus of basecourse = 𝑘 =
30kg/cm3, Maximum temperature differential at the location for pavement thickness value of 22,24,26
and 30cm are respectively14.8,15.6,16.2,16.8 0C, Desired factor of safety with respect to load stress and
wrapping stress at edge region is 1.1 to 1.2.
• Solution: P = 7500 kg, p = 7.5Kg/cm2, therefore radius ‘a’ = √
𝑃
𝑝𝜋
= √
7500
7.5𝑥𝜋
= 17.84 cm
• Trial 1, Assume pavement thickness h=25cm, Given K= 30kg/cm3, . E= 3.0x105 kg/cm2, 𝜇 = 0.15
• Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 3𝑥105𝑥253
12𝑥30 ( 1−0.152
)
= 60.41 cm,
• a/h = 17.84/25 = 0.7136< 1.724, Radius of the resisting section= b = 1.6𝑎2 + ℎ2 - 0.675h =
1.6 𝑋 (17.84)2 + 252 - (0.675x25) = 16.80 cm.
• Edge load stress, σe =
0.572 𝑃
ℎ2 [{4 log10 (l/b) +0.359 }] = 17.74 Kg/cm2
• For h= 25cm, temperature differential ( by interpolation) = (15.6+16.2) /2 = 15.9 0C
• Lx= 4.2m = 420cm Ly=375cm, So, wrapping stress for higher ratio = Lx/l = 420/60.41 = 6.96.

9. • From Bradbury wrapping stress coefficient chart Cx= 0.99, ∝ = 1𝑥10-5 0C
Wrapping stress at Edge region of the slab=
Cx E ∝ t
2
=
0.99𝑥 3𝑥 105𝑥10
−
5
𝑥15.9
2
= 23.61 kg/cm2
Total flexural stress Se + Ste = (17.74+ 23.61) = 41.35 kg/cm2 < 45 kg/cm2
Factor of Safety = 45/ 41.35 = 1.1. As the factor of safety obtained is within the desired factor of safety
between 1.1 to 1.2 so the adopted thickness for the rigid pavement 25 cm is Sufficient. Hence okay.
Example: The design thickness of a CC pavement is 26cm considering a design axle load ( 98th percentile load)
of 13000kg on single axle and M-40 concrete with characteristics compressive strength of 400 kg/cm2.The
relative stiffness is found to be 62.2 cm. If the elastic modulus of the dowel bar steel is 2x105Kg/cm2. Modulus
of dowel concrete interaction is 41500 kg/cm2 and joint width is 1.8cm, design the dowel bars for 40% load
transfer considering edge loading.
Solution: Radius of relative stiffness of pavement, l = 62.2 cm. Characteristics of compressive strength
(fck ) = 400 kg/cm2, Elastic modulus of the dowel bar steel is 2x105Kg/cm2 , Design load ( 98th percentile axle
load of single axle) =13000kg, Therefore design wheel load for dowel bar design P = 6500kg, Total load to be
sustained by the dowel bar group = 0.4P = 0.4x 6500 = 2600kg.
Let the maximum load sustained by the first dowel bar near edge =P1 kg.
Assume diameter of dowel bar = 3 cm and the spacing S= 25cm in the 1st Trail.
Substituting the relevant values , Moment of inertia of dowel bar = I = (𝜋b4/ 64)= 3.976 cm4

10. • Allowable bearing stress in concrete Fb = fck ( 10.16-b) / 9.525 = 400 (10.16-3) / 9.525 = 300.68 Kg/cm2 .
• Total load transferred by the dowel group for the assumed dowel diameter and spacing in terms of
maximum load carried:-
• Total load carried = P1 {1+(l-25)/l + (l-50)/l } = 1.794P1
• 1.794P1 = 2600 Kg, So, P1 = 1450Kg.
• Relative stiffness of dowel bars embedded in concrete = 𝛽 = (M b/4EI )0.25 = 0.25
• Check for maximum bearing stress between concrete and he dowel bar subs staining load, P1
• Sbm = M. P1 ( 2+ 𝛽 Z) / 4 𝛽3 Es I = 296.65 Kg/cm2. ( Joint Width Z=1.8cm)
• As the maximum bearing stress between concrete and dowel bar (296.65 Kg/cm2. ) < allowable bearing
strength in concrete (300.68 Kg/cm2 ) in the dowel bar design is safe and may be accepted .
• Rounded dowel bar of diameter 3 cm and spacing 25cm may be provided at expansion joints.

11. • Example: Design the dowel bars and their spacing from the following data:
• Wheel load=4000Kg, Modulus of subgrade reaction =6Kg/cm2, Modulus of Elasticity of concrete = 3x105
kg/cm2, Poisson’s ratio = 0.15, Slab thickness =20cm, Joint thickness= 18mm.
• Solution: Radius of relative stiffness = l = 4
{𝐸ℎ3/ 12K (1-𝜇2)} =
4 3𝑥105𝑥203
12𝑥6 ( 1−0.152
)
= 76.42 cm,
• Allowable bearing stress in concrete Fb = fck ( 10.16-b) / 9.525 = 400 (10.16-3.2) / 9.525 = 292 Kg/cm2
• ( The Grade of concrete assumed M40 Grade and Dia of Dowel bar ( assumed) = 3.2cm)
• Assumed spacing between dowel bars = 32 cm and First dowel bar is placed at a distance=15cm from
pavement edge. Assumed length of the dowel bar=50 cm.
• Dowel bars upto a distance of 1.0x radius of relative stiffness, from the point of load application are
effective in load transfer.
• No of dowel bars participating in the load transfer when wheel load is just over the dowel bar close to the
edge of the slab = 1+ (76.42/32) = 3 dowels
• Assuming that the load transfer by the first dowel is P1 and assuming that the load on the dowel bar at a
distance of l from the first dowel to be zero, the total load transferred by the dowel bar system =
• [ 1+ (76.42-32)/76.42 + ( 76.42-64)/76.42] . P1 = 1.75 P1
• Load carried by the outer dowel bar, P1 = 4000/1.75 = 2286 Kg.

12. • Check for bearing stress: Moment of Inertia of Dowel = I = (𝜋b4/ 64)= 5.147 cm4
• Relative stiffness of dowel bars embedded in concrete = 𝛽 = (Kb/4EI )0.25 =0.042
• Check for maximum bearing stress between concrete and he dowel bar subs staining load, P1
• Sbm = K P1 ( 2+ 𝛽 Z) / 4 𝛽3 Es I = 62.2 Kg/cm2. ( Joint Width Z=1.8cm) < 292 Kg/cm2
• Hence dowel bar spacing and diameter assumed are safe.

13. Example