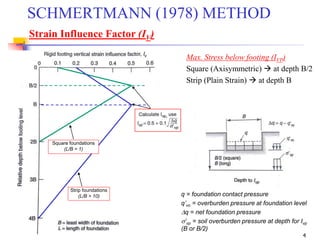
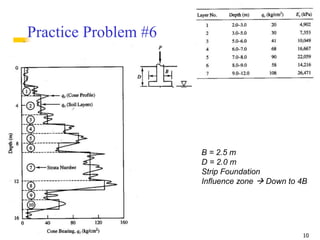
The document discusses the Schmertmann method for calculating vertical strain and settlement in sandy soils beneath foundations, detailing the equations and correction factors involved. Various examples, including practice problems and parameters like modulus of elasticity, are provided to illustrate the application of the method. References to foundational texts in geotechnical engineering are included for further reading.

1. 1
Geotechnical Engineering–II [CE-321]
BSc Civil Engineering – 5th Semester
by
Dr. Muhammad Irfan
Assistant Professor
Civil Engg. Dept. – UET Lahore
Email: mirfan1@msn.com
Lecture Handouts: https://groups.google.com/d/forum/geotech-ii_2015session
Lecture # 15
25-Oct-2017

2. 2
SCHMERTMANN (1978) METHOD
From elasticity theory;
𝜀 𝑣 =
∆𝑞
𝐸𝑠
𝐼𝑣
Where,
eV = vertical strain
Dq = net foundation contact pressure (kN/m2)
ES = Modulus of elasticity of sand (Young’s Modulus) (kN/m2)
IV = Strain influence factor for soil beneath foundation
Settlement
Where,
Dz = Thickness of compressible layer
Semi-empirical approach  theory + model studies for vertical
strain in sands below foundation as function of depth
Semi-empirical approach
𝑆 𝑒 = 𝜀 𝑣 ∙ ∆𝑧

3. 3
SCHMERTMANN (1978) METHOD
C1 = Correction factor to compensate for the effects of foundation depth
(or embedment)
C2 = Correction factor for creep and other time dependent deformations
𝑆 𝑒 =
∆𝑞
𝐸𝑠
𝐼𝑣 ∙ ∆𝑧𝑆 𝑒 = 𝜀 𝑣 ∙ ∆𝑧
Correction Factors
𝐶1 = 1 − 0.5
𝑞 𝑣𝑜
∆𝑞 𝐶2 = 1 + 0.2 log 10𝑡
Where,
qVO = soil overburden pressure at base of foundation (kN/m2)
t = Elapsed time (years)
𝑆 𝑒 =
∆𝑞
𝐸𝑠
𝐼𝑣 ∙ ∆𝑧 ∙ 𝐶1 𝐶2
?Next slide

4. 4
SCHMERTMANN (1978) METHOD
Strain Influence Factor (IV)
Square foundations
(L/B = 1)
Strip foundations
(L/B > 10)
Max. Stress below footing (IVP)
Square (Axisymmetric)  at depth B/2
Strip (Plain Strain)  at depth B
q = foundation contact pressure
q’vo = overburden pressure at foundation level
Dq = net foundation pressure
s’vp = soil overburden pressure at depth for Ivp
(B or B/2)

5. 5
Practice Problem #5
A square footing 3 m by 3 m is resting on a sand deposit shown
in the figure. Assuming the modulus of elasticity of the sand to
be equal to 2.5qc, determine the elastic settlement of foundation
5 years after construction using Schmertmann method.

6. 9
Practice Problem #6
The results of a CPT sounding
performed at a site are shown in
figure. The soils consist of young
normally consolidated sands with
interbedded silts. The groundwater
table is at a depth of 2.0 m below the
ground surface.
A 375 kN/m load is to be supported
on a 2.5 m x 30 m footing to be
founded at a depth of 2.0 m in this
soil. Use Schmertmann’s method to
compute the settlement of this footing
soon after construction and the
settlement 50 years after construction.
Use Es = 2.5 qc; g = 17 kN/m3 (above
WT), and g = 20 kN/m3 (below WT)

7. 10
Practice Problem #6
B = 2.5 m
D = 2.0 m
Strip Foundation
Influence zone  Down to 4B

8. 12
CONCLUDED
REFERENCE MATERIAL
Foundation Analysis and Design (5th Ed.)
Joseph E. Bowles
Chapter #5
Principles of Geotechnical Engineering (7th Ed.)
Braja M. Das
Chapter #11
Essentials of Soil Mechanics and Foundations (7th Ed.)
David F. McCarthy
Chapter #10
(Schmertmann Method)
(Timoshenko & Goodier Method)
(Modified Mayerhof Method)