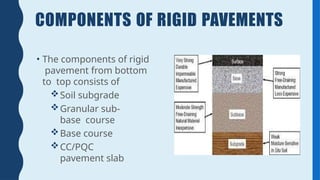
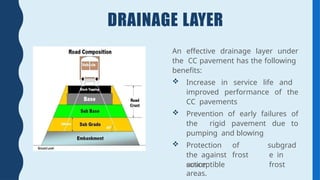
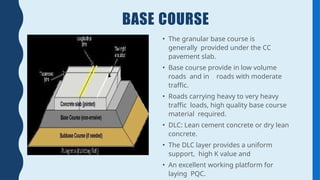
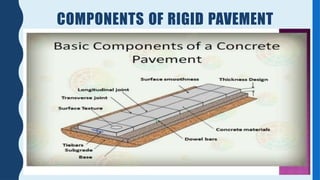
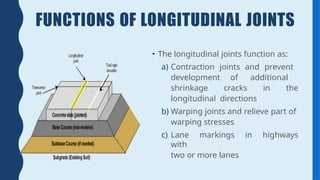
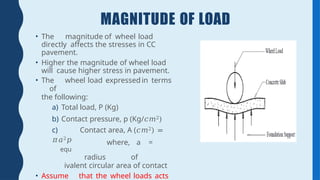
Rigid pavement analysis and design: Factors controlling rigid pavement design, types of stresses in rigid pavements, critical load positions, load stresses and temperature stresses in interior, corner and edge locations of jointed plain cement concrete pavement slabs, IRC 58-2015 method of rigid pavement design; Overlay Designs: Types of overlays on flexible and rigid pavements.

1. NNRG College of Engineering
DEPARTMENT OF CIVIL ENGINEERING
TRANSPORTATION
ENGINEERING
Unit-5
Presented by:
MOOD NARESH
ASST.PROF
nnrg

2. RIGID
PAVEMENTS

3. RIGID PAVEMENT
• The pavements which possess flexural
strength, are called as rigid pavements.
• The rigid pavements are generally made of
Portland cement concrete and some times
called as ‘CC Pavements’.
• The cement concrete used for rigid
pavements is called as ‘Pavement Quality
Concrete (PQC)’.
• The CC pavement slabs made of PQC
are
generally expected to sustain up to
45kg/𝑐𝑚2
of flexural stresses.
• The rigid or CC pavements are designed
and constructed for a design life of 30
years.

4. WHERE RIGID PAVEMENT NEEDED?
• Rigid pavements are usually
provided under the circumstances:
 Very heavy rainfall
 Poor soil conditions
 Poor drainage
 Extreme climatic conditions
 Combination of some of these
conditions which may lead to
development of cracks in
pavements.

5. STRUCTURE OF RIGID PAVEMENT

6. COMPONENTS OF RIGID PAVEMENTS
• The components of rigid
pavement from bottom
to top consists of
Soil subgrade
Granular sub-
base course
Base course
CC/PQC
pavement slab

7. SUBGRADE SOIL
• The subgrade soil of rigid pavements
consists of natural or selected soil from
identified locations fulfilling specified
requirements.
• Should contain require density and
other
engineering properties.
• Subgrade ultimately supports all layers of
rigid pavement and traffic loads.
• The compressive stresses transmitting
to
subgrade are very low.
• No need to consider allowable vertical
strains.

8. SUBGRADE
• The strength of soil subgrade is
generally
evaluated by adopting plate load test.
• Relatively using a large diameter plate.
• The load supporting capacity of the
subgrade is assessed in terms of
modulus of subgrade reaction, K.
• Modulus of subgrade reaction, K may be
defined as the pressure sustained per
unit deformation of subgrade at
specified deformation or penetration,
using specified plate size (75cm).
• But for highway pavements, plate of
30cm is used

9. GRANULAR SUB & DRAINAGE LAYER
• The granular sub-base course (GSB) serve
as drainage layer.
• To prevent early failures due to
excessive
moisture in the subgrade soil.
• Crushed stone aggregates are preferred
in the granular sub-base course, contains
high permeability.
• Coarse graded aggregates with low % of
fines (<5.0% finer than 0.075mm size) will
serve as a good drainage layer.

10. DRAINAGE LAYER
An effective drainage layer under
the CC pavement has the following
benefits:
 Increase in service life and
improved performance of the
CC pavements
 Prevention of early failures of
the rigid pavement due to
pumping and blowing
 Protection of
the against frost
action
subgrad
e in
frost
susceptible
areas.

11. BASE COURSE
• The granular base course is
generally provided under the CC
pavement slab.
• Base course provide in low volume
roads and in roads with moderate
traffic.
• Roads carrying heavy to very heavy
traffic loads, high quality base course
material required.
• DLC: Lean cement concrete or dry lean
concrete.
• The DLC layer provides a uniform
support, high K value and
• An excellent working platform for
laying PQC.

12. PQC PAVEMENT SLAB
• M-40 cement concrete mix with a
minimum flexural strength of 45 kg/𝑐𝑚2
is to be used.
• The CC pavement slab should withstand
the
flexural stresses caused by
1) Heavy traffic loads
2) Wrapping effects due to temperature
• High quality CC mix with high flexural
strength is used for the construction of
the PQC slab.
• Using steel reinforcement is not to
bear flexural/ tensile stresses
developed.

13. RIGID PAVEMENT
 Subgrade
 Sub-base
 Base
 Separation layer
 PQC pavement
 Joints in CC pavements
A separation layer
consisting of a
suitable
base course before laying PQC slab in order
to prevent bonding between two.

14. COMPONENTS OF RIGID PAVEMENT

15. JOINTS IN RIGID PAVEMENT
• Joints are important components in
CC pavements and they have
important functions to perform.
• Main purpose of joints is to
relieve part of the stresses
developed due to the temperature
variations in the slabs.
• The joints in CC pavements are:
a) Longitudinal joints
b) Transverse joints

16. LONGITUDINAL JOINTS
• In pavements of width of 4.5m, there is a
need to provide a longitudinal joint.
• The need of these longitudinal joints is
to prevent the shrinkage cracks,
happening during the initial period of
curing.
• However, as the lane of width is
generally 3.5m to 3.75m, longitudinal
joints provided between each traffic
lane.
Note:
Shrinkage cracks develop in slabs
whose width or length is more than 4.5
to 5m.

17. LONGITUDINAL JOINTS
• Tie bars are provided along
the longitudinal joints, in
order to prevent opening up
of the longitudinal joints in
due course.
• These tie bars of specified
diameter and length are
embedded at the specified
spacing, at the mid depth of the
pavement slab.

18. FUNCTIONS OF LONGITUDINAL JOINTS
• The longitudinal joints function as:
a) Contraction joints and prevent
development of additional
shrinkage cracks in the
longitudinal directions
b) Warping joints and relieve part of
warping stresses
c) Lane markings in highways
with
two or more lanes

19. TRANSVERSE JOINTS
• The transverse joints
are subdivided into
three categories, based
on their purpose:
a) Contraction joints
b) Expansion joints
c) Construction joints

20. CONTRACTION JOINTS
• Contraction joints are formed by cutting
grooves across the pavement slab at
regular intervals.
• Width of grooves – not less than 3mm
• Depth of grooves – 25 to 30% of
pavement
thickness
• Spacing of two contraction joints – 4 to 5m.
• The shrinkage cracks formed below the
each groove at the weekend section,
during the initial period of curing.
• Any how, shrinkage cracks formed at
regular intervals, to prevent those cracks,
contraction joints were provided.

21. CONTRACTION JOINTS
• Any how, shrinkage cracks
developed along these
predetermined sections only.
• In order to prevent widening of
these fine shrinkage cracks, steel
reinforcement may be provided
across the contraction joints.
• If no reinforcement provided across
the contraction joints, such a
pavement is – ‘pain jointed
concrete pavement’.
• Closely spaced contraction joints
help to relieve part of the warping
stresses developed.

22. EXPANSION JOINTS
• CC pavement slabs, during the summer
get expanded & during winter gets
contracted.
• To accommodate these variations in
length, expansion joints are provided in
transverse pavement at long intervals.
• The expansion joints are formed as
through joints across the full depth of
the slab with about 20mm gap
between the two slabs.
• The expansion joints provided after a
number of contraction joints

23. EXPANSION JOINTS
• The CC pavement slab is
separated across the expansion
joint, therefore there is no load
transfer across the expansion
joint.
• Week cross section of the CC
pavement.
• In order to strengthen these
sections and to provide load
transfer across the expansion
joint, suitable dowel bars are
designed and installed during
construction.

24. CONSTRUCTION JOINTS
• Construction joints formed due to gaps between
the
continuous construction works.
• During the construction of CC pavements when
the concreting work is stopped at the end of
the day, the concrete paving is suspended, a
construction joint is formed.
• Construction joints formed across the
pavement, about full depth.
• It is necessary to provide dowel bars across
these
joints for load transfer.
• It is better to make a construction joint as
expansion joint or contraction joint, if possible.

25. COMPONENTS OF RIGID PAVEMENT

26. FACTORS AFFECTING OF RIGID
PAVEMENT
• The factors which affect the design and performance of rigid pavement
or CC pavements are listed below:
a) Wheel load
b) Temperature variations at the location of the road
c) Types of joints and their spacing
d) Sub-grade and other supporting layers

27. FACTORS AFFECTING DESIGN
• The two major factors primarily to
be considered for the design of
rigid pavement are:
a) Heavy traffic loads
b) Temperature variation
between top and bottom of
the CC pavement slab
• The other factors which affect
the design and performance
of rigid pavements are,
a) Temperature stresses due to
expansion and contraction of
rigid pavement during
summer and winter
b) Volumetric changes in
subgrade due to changes in
moisture and temperature
c) Loss of subgrade support due
to some reasons at some
locations

28. WHEEL LOAD
• The performance of rigid pavement
and its service life depends on the
actual magnitude of the heaviest
wheel loads of vehicles and their
number of repetitions during the
design life.
• The wheel loads of highest magnitude
cause, flexural stresses in rigid
pavement.
• The important factors associated with
wheel loads are:
Location of the loading on the
CC
pavement
slab
a) Magnitude of load/
contact pressure of loaded area
b)
c) Repetitions of loads of
different
magnitudes during the design
life

29. MAGNITUDE OF LOAD
• The magnitude of wheel load
directly affects the stresses in CC
pavement.
• Higher the magnitude of wheel load
will cause higher stress in pavement.
• The wheel load expressed in terms
of
the following:
a) Total load, P (Kg)
b) Contact pressure, p (Kg/𝑐𝑚2)
c) Contact area, A (𝑐𝑚2) =
𝜋𝑎2𝑝
equ
where, a =
radius of
ivalent circular area of contact
• Assume that the wheel loads acts

30. LOCATION OF LOAD APPLICATION ON SLAB
• The load stresses on slab are vary depending upon the location on
which the wheel load acts.
• Following three locations are considered in the analysis and design of
CC pavements:
a) Interior load, ‘i’ applied at a location away from the edges of the slab
b) Corner load, ‘c’ applied at the corner region of the slab
c) Edge load, ‘e’ applied at the edge region of the slab
• The magnitude of stress due to a given wheel load applied at the corner
region is the highest in comparison to the stresses due to the same load
applied at the edge or interior region of a CC pavement.
• The load stress applied at the interior region of a CC pavement, away from
the edges is found to be the lowest in comparison to the stresses due to
same load applied at the edge and corner regions of the pavement.

31. REPETITIONS OF LOADS
• The repeated application of light loads do not cause any structural deterioration
to roads. Therefore it is essential to measure the loads of higher magnitude
which could cause significant stress levels in the rigid pavement.
• For design of rigid pavement, it is essential to
a) Estimate the actual magnitude of heavier groups of axle or wheel loads
b) Determine the flexural stresses developed due to these heavy loads
c) Estimate the number of repetitions of each load group to use the road
during the design life
• Repeated application of high magnitudes of stresses are, to cause failures
due to
fatigue in CC pavement structures.
• The plain CC specimens or slabs can withstand against number of repetitions of
load to cause stresses, if the magnitude of applied stress is less than 44% of its
flexural strength.

32. STRESS RATIO
• The ratio of flexural stresses due
to a load applied on a CC
pavement to its flexural strength
is called the ‘stress ratio’.
• From the fatigue studies on CC
pavements, number of
repetitions up to fatigue failure,
have been determined by using
various values stress ratio
between 0.45 to 0.90.
• While designing a CC pavement,
if stress ratio is less than 0.44,
there is no possibility of fatigue

33. STRESS RATIO
load would cause, lower
stress
ratios.
• Hence, there will be no structural
deterioration of the pavement due
to these loads.
• The design wheel load should
be
carefully decided taking into
account wheel load distribution
studies and the expected no. of
repetition of loads of different
magnitudes during the design life
IMPORTANCE OF DESIGN LOAD
• The repeated application of any • The
movement
of even a
small
loads of magnitude less than design number
excessively
ove
r
loade
d
vehicles with higher magnitude
of
loads than
the
develop
tensile
desig
n
crack
s
load,
can
at
some
locations of the CC
slab.
• It is suggested that, axle
load
studies should be conducted on
heavy vehicles in order to arrive
at the design axle load.
• It is necessary to estimate the
possible movement of over loaded
vehicles with loads exceeding the

34. AXLE LOAD DISTRIBUTION STUDIES
• Axle load or wheel load distribution studies are carried out on the
selected heavy vehicles, that actually moving on the existing roads.
• It is also desirable to note the wheel base or spacing between the
axles
of the heavy commercial vehicles (HCV).
• The objectives of the study are
a) To arrive at the design load
b) To assess the effect of repeated application of stresses due to
loads that are heavier than the selected design load which
cause stress ratios exceeding 0.44 and the number of
repetitions of such heavier loads expected during the design
life.
• These data are necessary at the design stage for the fatigue

35. DETERMINATION OF DESIGN LOAD
• First of all complete the measurement of axle/ wheel loads on
the selected samples of heavy vehicles (with single, tandem and
multiple axles) at the identified locations.
• Axle load distribution table is prepared, by groping the
loads at convenient load intervals or ranges.
• The average of each load group is taken as the magnitude of the
applied load and the expected no. of repetitions of the vehicles of
each range during the design life is estimated.
• The total number of axle loads of each interval noted during
project preparation studies are noted as the initial traffic.

36. CONTD.,
• Considering the different vehicle classes, their growth rate,
construction period and design life of the CC pavement, the total
number of repetition of loads of each group load during design life
of the CC pavement are estimated.
• Based on the above data, the cumulative frequency distribution
table or diagram (representing load values and the total number of
repetitions during design life) is prepared.
• From this table or diagram, 98th percentile load (which will be
exceeded by only by 2.0%) may be taken as the ‘Design load’.
• It is also desirable to consider a ‘load safety factor’ of about
1.2 to
account for the possibility of further over loading of the heavy
vehicles.

37. DAILY VARIATION IN TEMPERATURE
• The daily variation in atmospheric
temperature causes difference in
temperature between the top and
bottom of the CC pavement slab.
This results in warping of slab and
development of flexural stresses.

38. TEMPERATURE DURING DAY
• The temperature difference between
the top and bottom of the CC
pavement results in differential
expansion the slab causing it to
warp or bend.
• The temperature difference during
day
is given by:
𝑡0C = (𝑡1 −
𝑡2)0C
where,
𝑡1= maximum temperature at top of
the pavement during day
𝑡2 = the temperature at the bottom
of
the pavement during night

39. TEMPERATURE DURING NIGHT
• At late night top of the slab
becomes colder resulting in
warping of the slab.
• The temperature difference during
day is given by:
𝑡0C = (𝑡1 − 𝑡2)0C
where,
𝑡1= minimum temperature at top of
the pavement during night
𝑡2 = the corresponding temperature at
the bottom of the pavement during
night

40. NO WARPING CONDITION
• During the two short
durations with in 24 hours,
the temperatures at top and
bottom of the slabs are equal,
no warping will takes place.
• This stage of the CC
pavement is called as ‘no
warping condition’ of the
pavement.

41. STRESSES IN RIGID PAVEMENT
• Different types of stresses developed in CC pavements. The major types of
stresses in CC pavements consists of:
a) Wheel load stresses caused by heavy wheel loads
b) Warping stresses caused by temperature differential between
the top and bottom of the pavement.
• It is possible to determine the stresses developed due to wheel loads, warping
and contraction of CC slab and it not possible estimate the magnitude of stresses
as result of volumetric changes in subgrade.

42. WHEEL LOAD STRESSES
• Westergaard gave theoretical formulae to determine the stresses
caused due to wheel load applying on the rigid pavements.
• For this he carried out the following assumptions on rigid pavements:
a) Cement concrete slab is homogeneous
b) It is thin plastic plate
c) The subgrade reaction being vertical and proportional to the
deflection
• Westergaard’s equations for stresses due to wheel load applied at the
three
critical locations of interior, edge and corner as given below:

43. CONTD.,
• Load stress, Si due to interior
loading,
S =
0.316
P
h2
1
0
b
4log (l/ ) +
1.069
i
• Load stress, Se due to edge
loading,
Se =
0.572
P
h2
1
0
b
4log (l/ ) +
0.359
• Load stress, Sc due to corner
loading,
3
𝑃
𝑎
2𝑙
0.
6
Here
,
Sc = ℎ2
1 −
h = slab thickness, cm
P = Wheel load, kg
a = radius of wheel load distribution,
cm l = radius of relative stiffness, cm
b = radius of resisting section

44. CONTD.,
• Maximum stress produced by a wheel at corner does not exist around the load,
but it occurs at some distance X along the diagonal. This distance X from the
corner is given by the relation
X = 2.58 𝑎𝑙
Here,
corne
r
X = distance from apex of slab corner to section of maximum stress
along the bisector or diagonal, cm
a = radius of wheel load distribution,
cm l = radius of relative stiffness,
cm

45. CONTD.,
Radius of relative stiffness:
• Westergaard defined, ‘radius of relative stiffness’, l which is expressed by the
equation,
l
=
𝐸ℎ
3
12𝐾
1−µ2
1/
4
Here,
l = radius of relative stiffness, cm
h = slab thickness, cm
E = modulus of elasticity of cement concrete,
kg/cm2
µ = Poisson’s ratio for concrete = 0.15
K = modulus of subgrade reaction, kg/cm3

46. CONTD.,
Equivalent radius of resisting section:
• According to Westergaard, the equivalent radius of resisting section is
approximated, in terms of radius of load distribution and slab thickness,
b = 1.6a2 + h2 −0.675h
Here,
b = equivalent radius of resisting section, cm when ‘a’ is less than
1.724h a = radius of wheel load distribution, cm
h = slab thickness, cm
When ‘a’ is greater than 1.724h, b =
a

47. TEMPERATURE STRESSES
• Two types of stresses are produced due to temperature variations in
concrete pavements:
a) Warping stresses due to temperature differential between
the top and bottom of the pavement as a result of daily
variation in temperature at the location and
b) Frictional stresses due to over all increase or decrease in
temperature of the pavement slab as a result of seasonal
variation in temperature at the location

48. WARPING STRESSES
• Warping stress at interior, 𝑆𝑡(𝑖) is given
by,
(𝒊
)
𝑺𝒕 = 𝑬𝒆𝒕
𝑪𝒙+µ𝑪𝒚
𝟐
𝟏−µ𝟐
• Warping stresses at the edge, 𝑆𝑡(𝑒) is given
by,
(𝒆
)
𝑺𝒕 = �
�
𝑪
𝑬𝒆𝒕 o
r
�
�
𝑪
𝑬𝒆𝒕
𝟐
𝟐
(whichever is
higher)
• Warping stresses at corner, 𝑆𝑡(𝑐) is given
by,
(𝒄
)
𝑺𝒕 =
𝑬𝒆𝒕
𝒂
𝟑(𝟏−µ) 𝒍

49. CONTD.,
Here,
E = modulus of elasticity of concrete
e = thermal coefficient of concrete per degree centigradeType
equation here.
t = temperature differential between the top and bottom of the slab
µ = Poisson’s ratio of cement concrete
𝐶𝑥 = coefficient in direction X which depends on the
ratio,
𝐿
𝑥𝑙
𝐶𝑦 = coefficient in direction Y which depends on the
ratio,
𝐿
𝑦
𝑙

50. FRICTIONAL STRESSES
𝑆𝑓 =
𝑊𝐿𝑐𝑓 /
2 × 104
Here,
𝑠𝑓 = stress developed due to inter-face friction in cement concrete
pavement per
uni
t
area, kg/cm2
W = unit weight of concrete (about 2400 kg/cm3)
f = coefficient of friction at the interface (maximum value is about
1.5)
Lc = spacing between the contraction joint = slab length, m
B = slab width

51. DESIGN OF RIGID PAVEMENT
• The design wheel load is first decided on relevant axle load studies and analysis.
• Based on the locality where the pavement is to be constructed, the
temperature differentials for pavement thicknesses are estimated.
• The supporting layers of the rigid pavement such as subgrade, sub-base
layer and base course layers are decided and the subgrade modulus is
either determined or estimated.
• The spacing between the longitudinal joints, Lc to provided, during the initial
period of curing.
• A trial thickness of pavement is first assumed, the load and warping stress values
at pavement edge are determined using the appropriate stress equations. If
total value of stress exceed the permissible limit, the trial is repeated assuming a
higher pavement thickness.
• The factor of safety of the trial thickness of the pavement is worked out by
taking the ratio of flexural strength to flexural stresses.

52. CONTD.,
• Design life should be estimated.
• If the stress ratios exceeding 0.44 due to the higher loading are
noted and then fatigue analysis is carried out based on the number
of repetitions during the design life.
• If the assumed thickness is failed, the next trail is made after
suitably revising the thickness.
• The total of the edge load stress due to the heaviest load and the
edge warping stress on summer mid day is calculated, if the total
thickness is less than flexural strength of CC (45 kg/cm2), the design
is accepted; otherwise the thickness is further revised until the
highest possible total stress value does not exceed the flexural
strength.