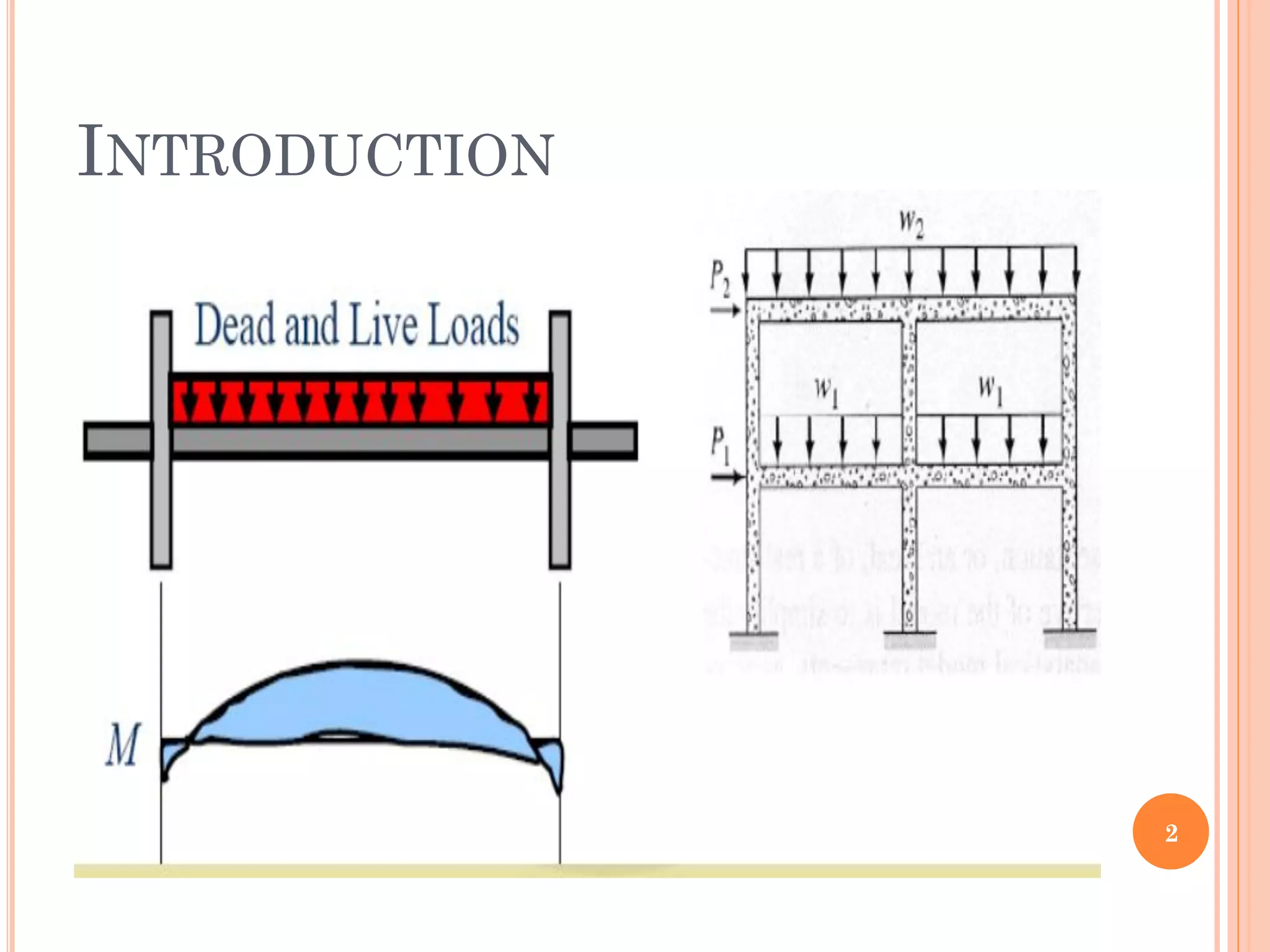
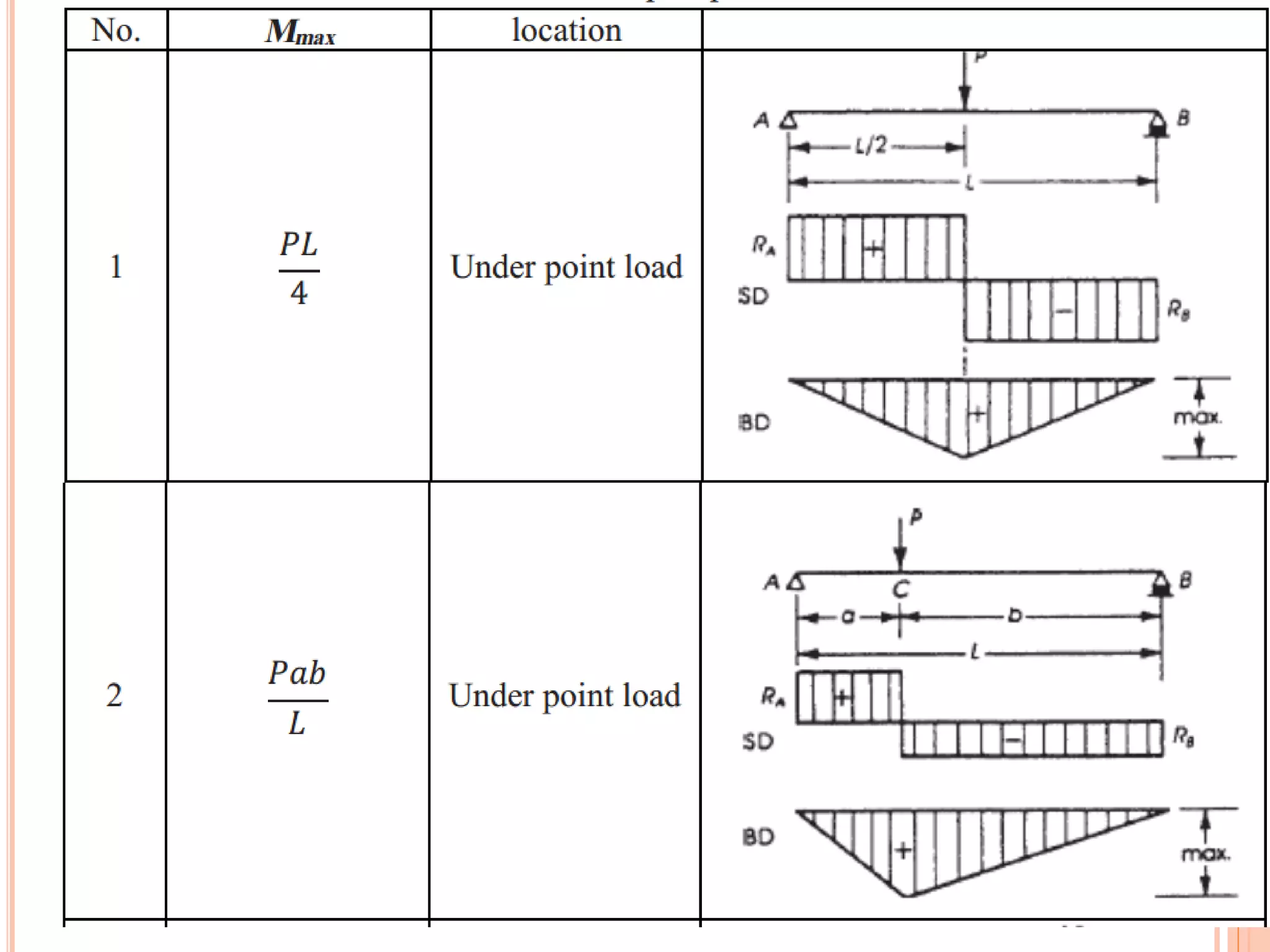
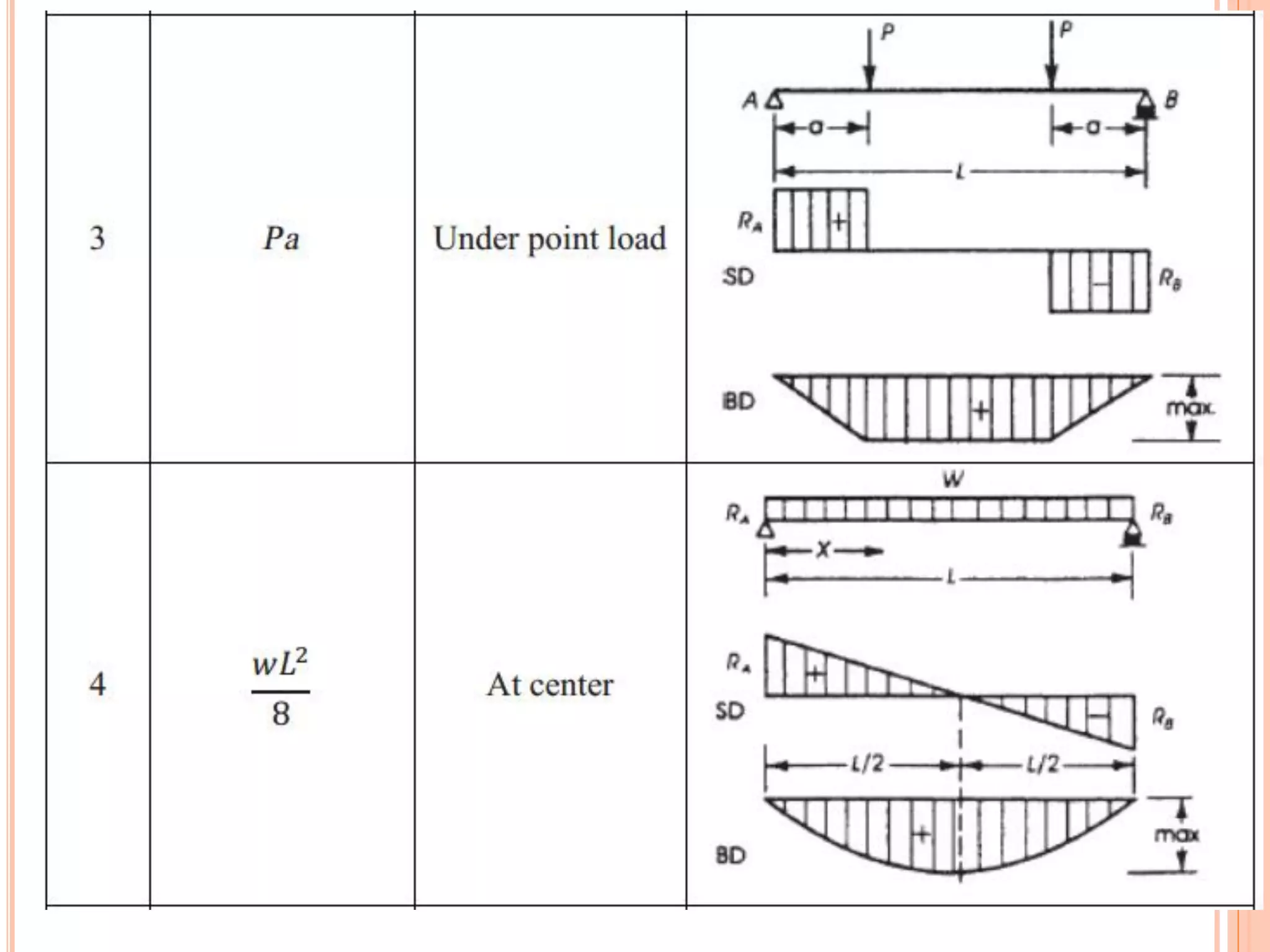
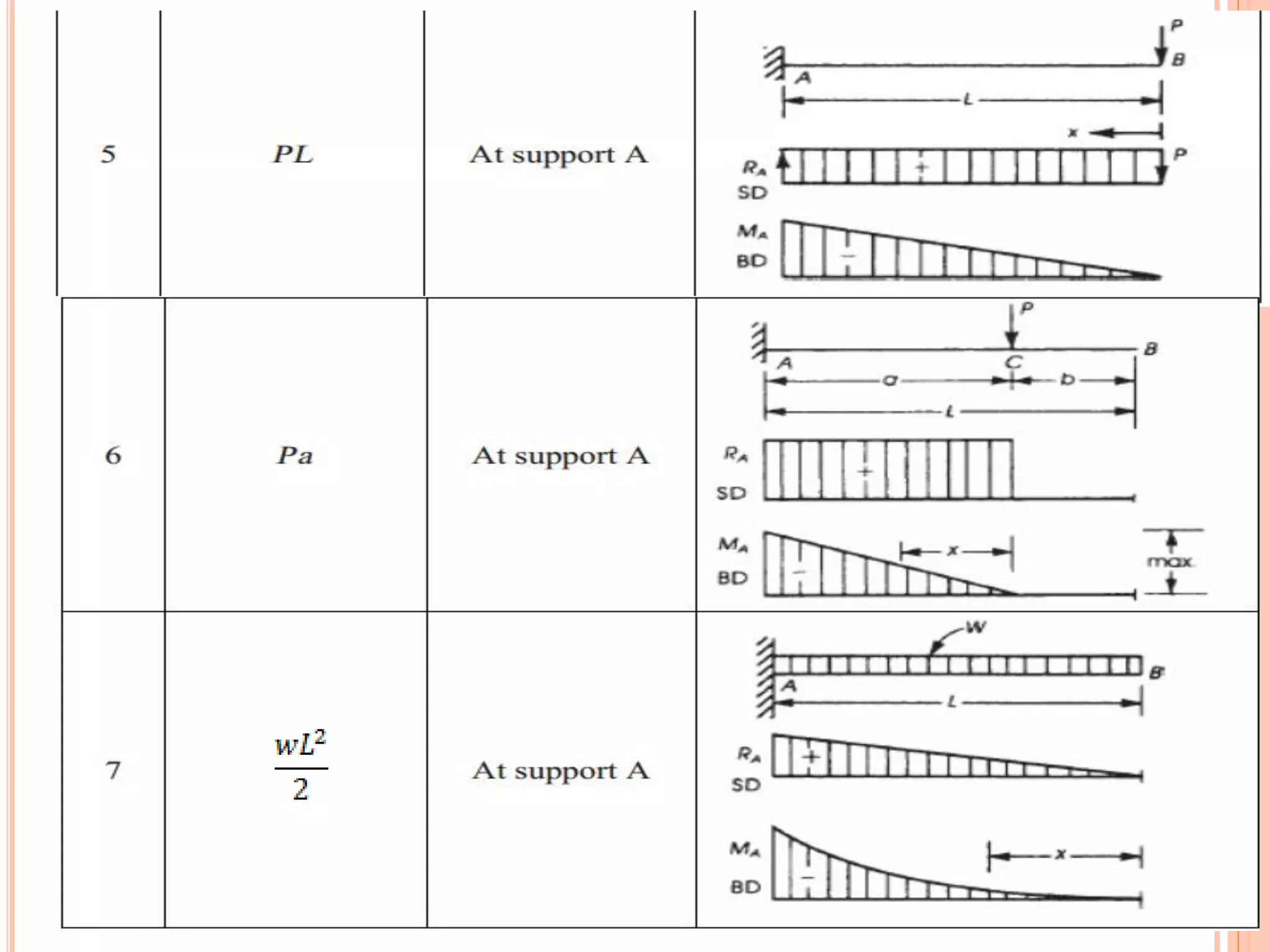
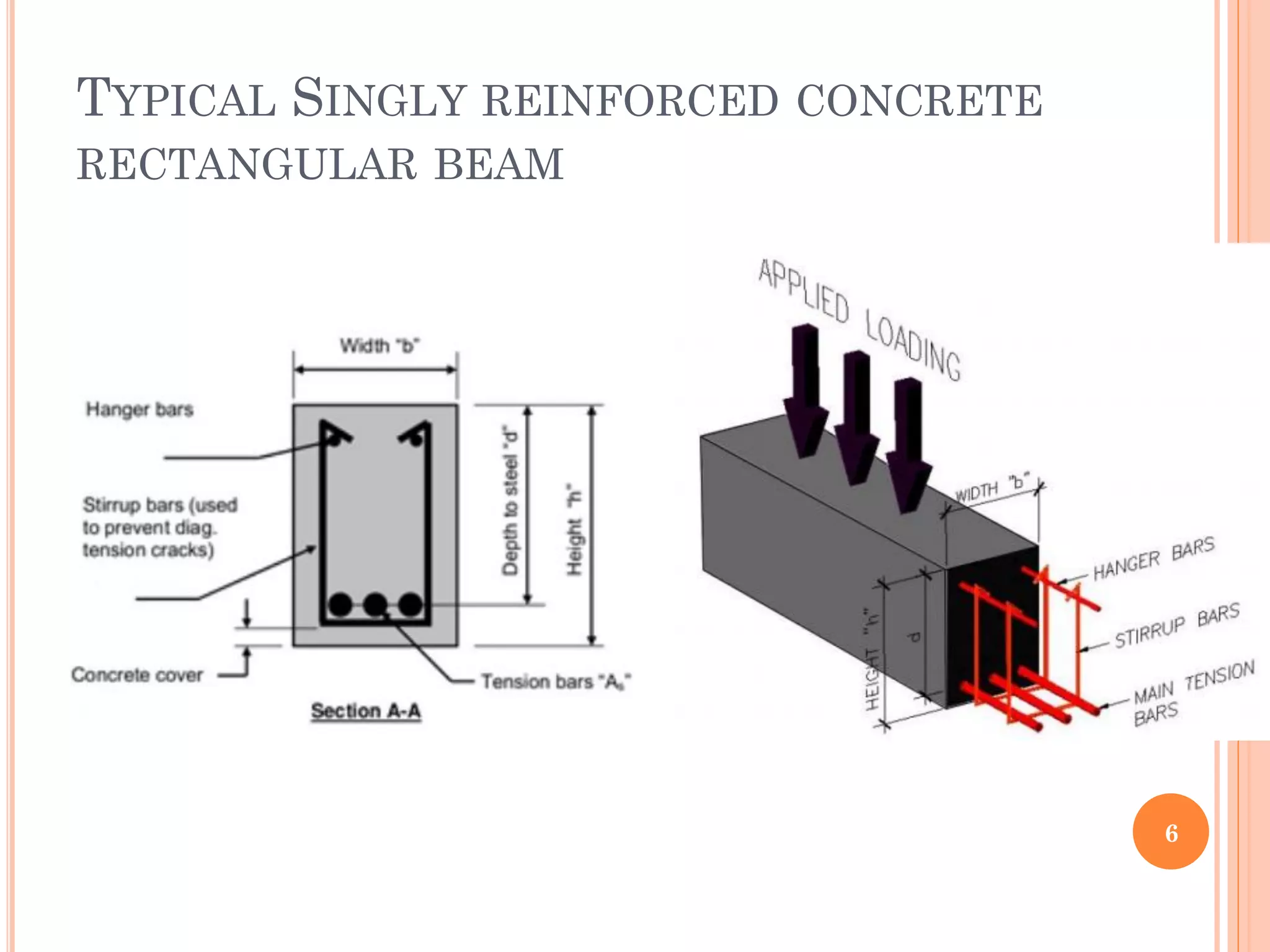
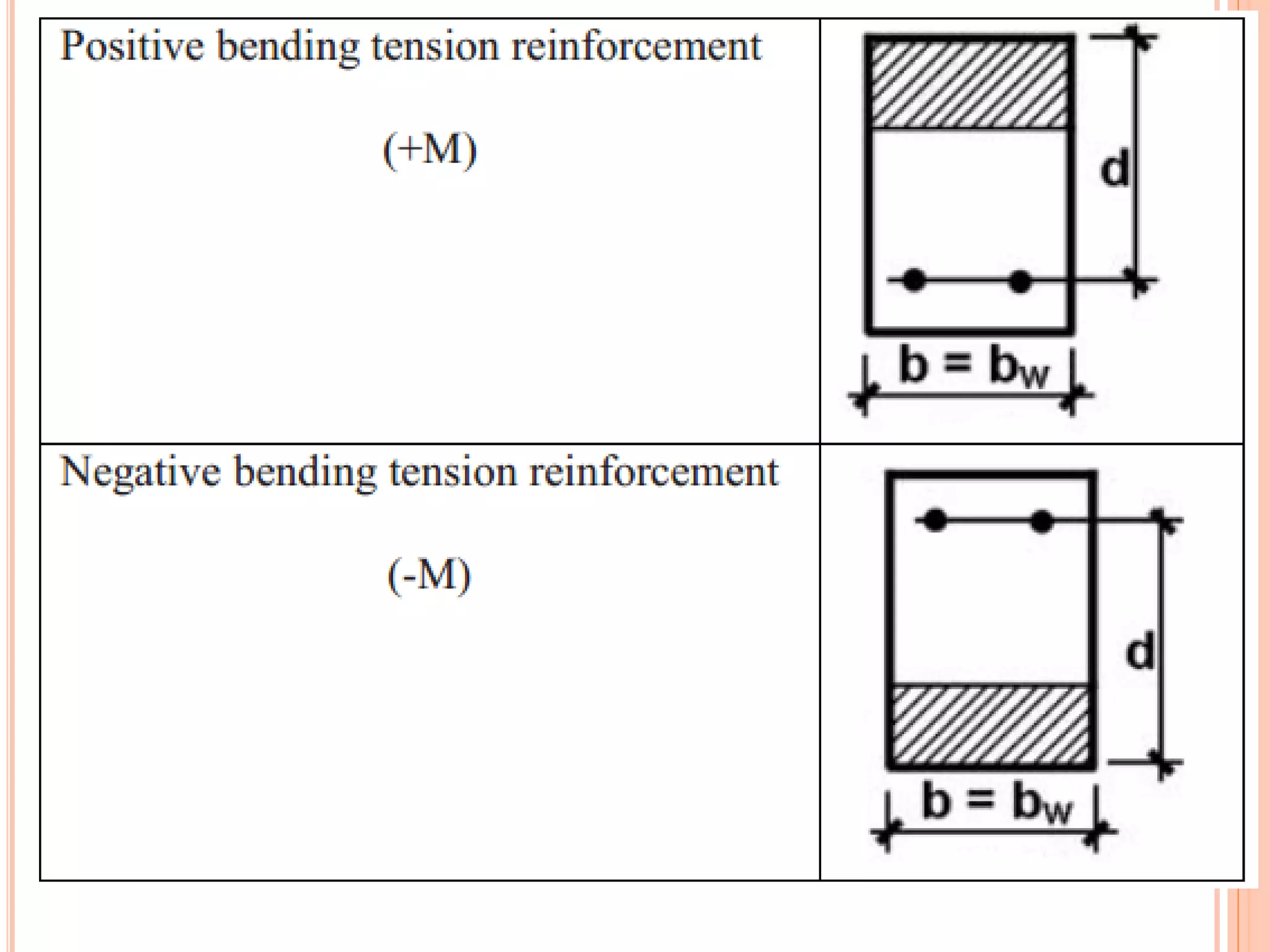
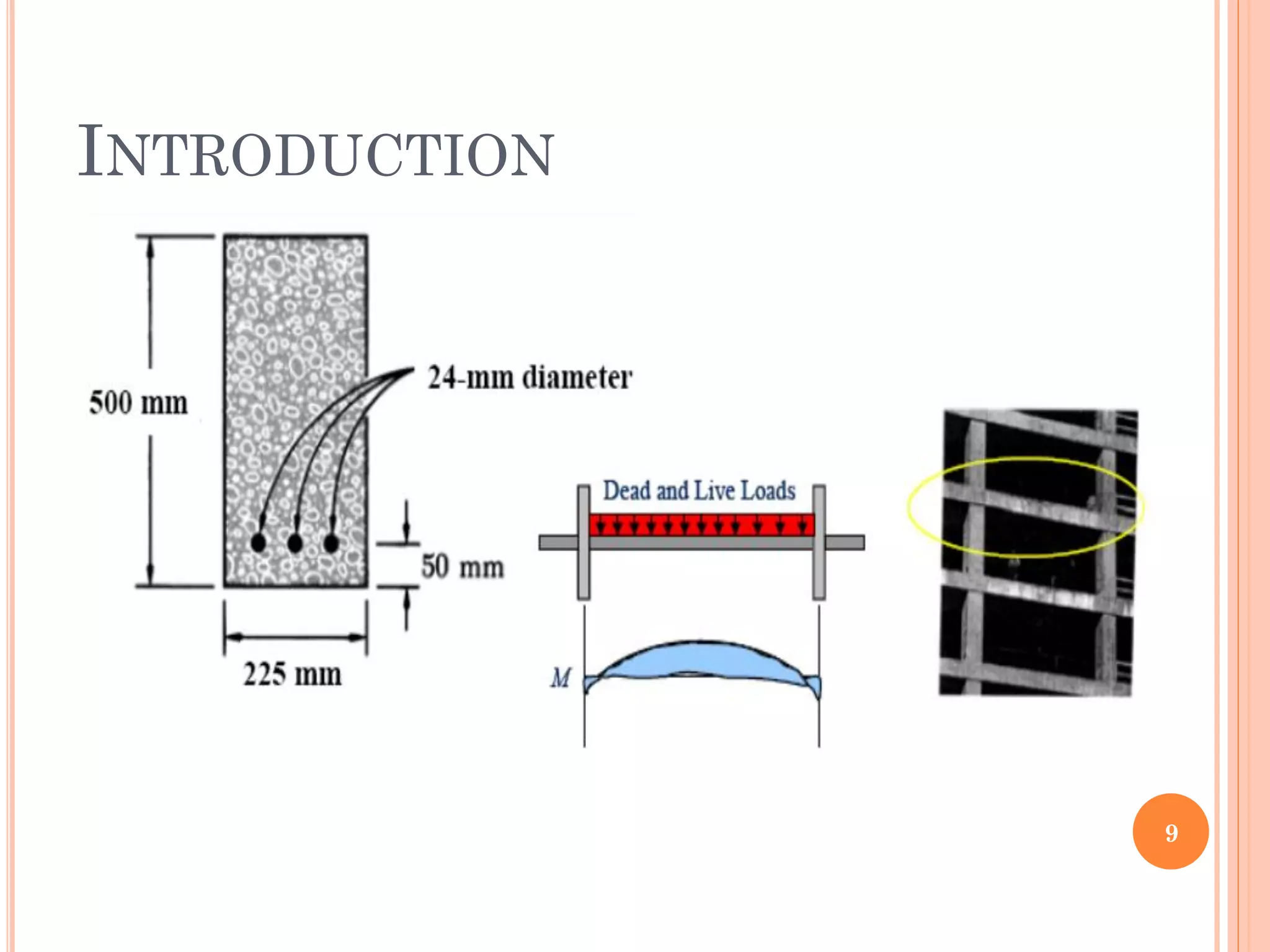
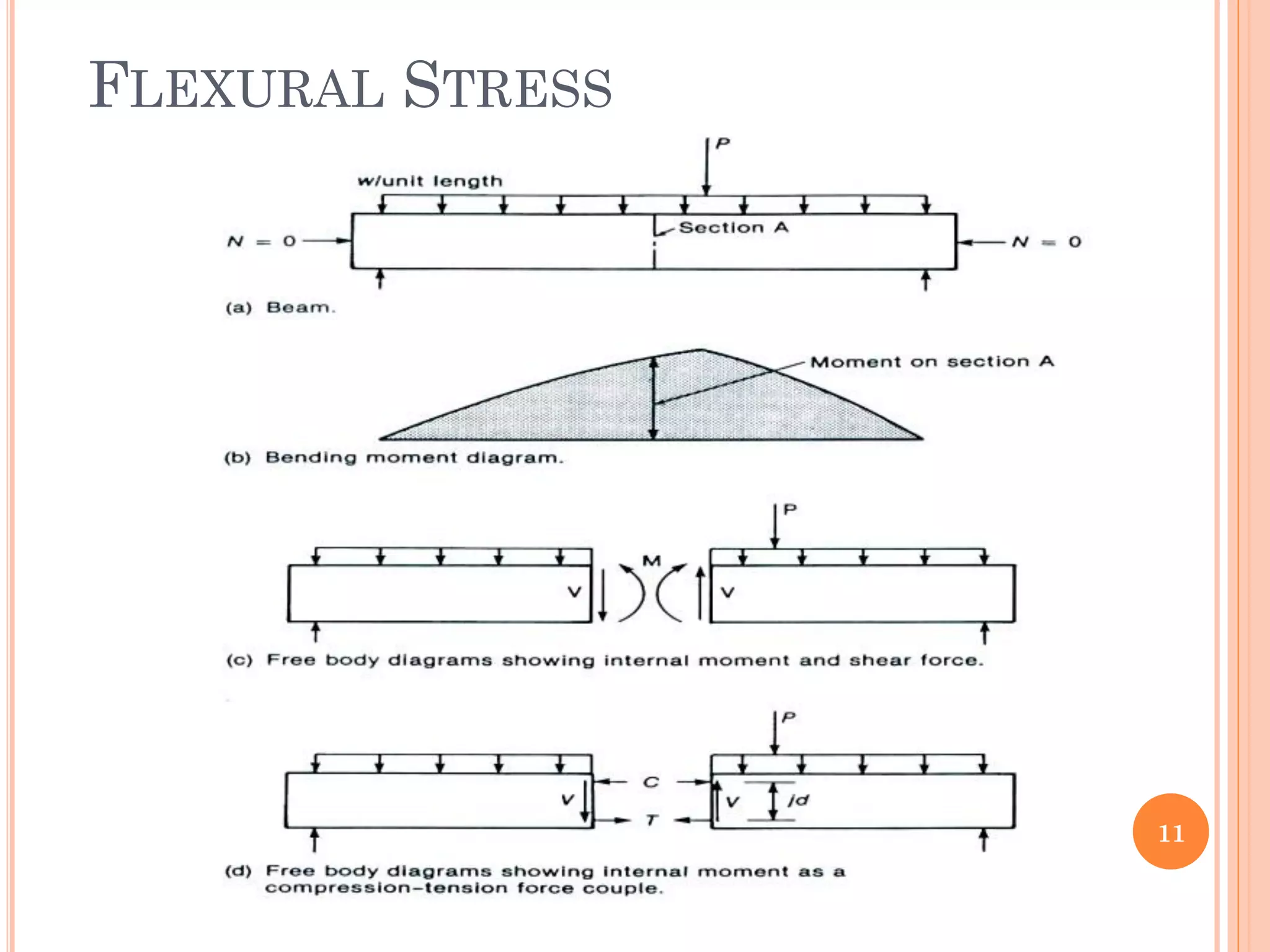
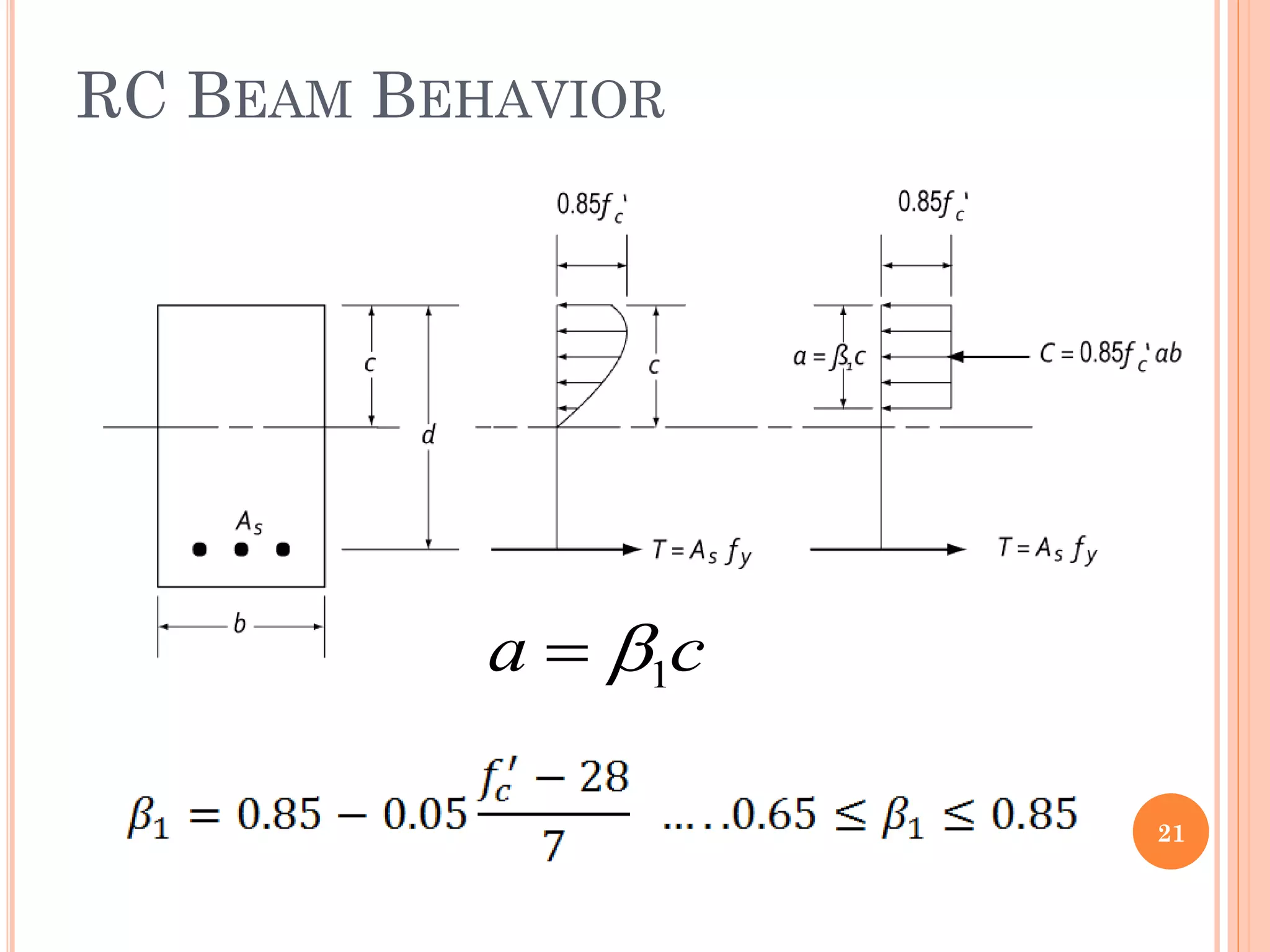
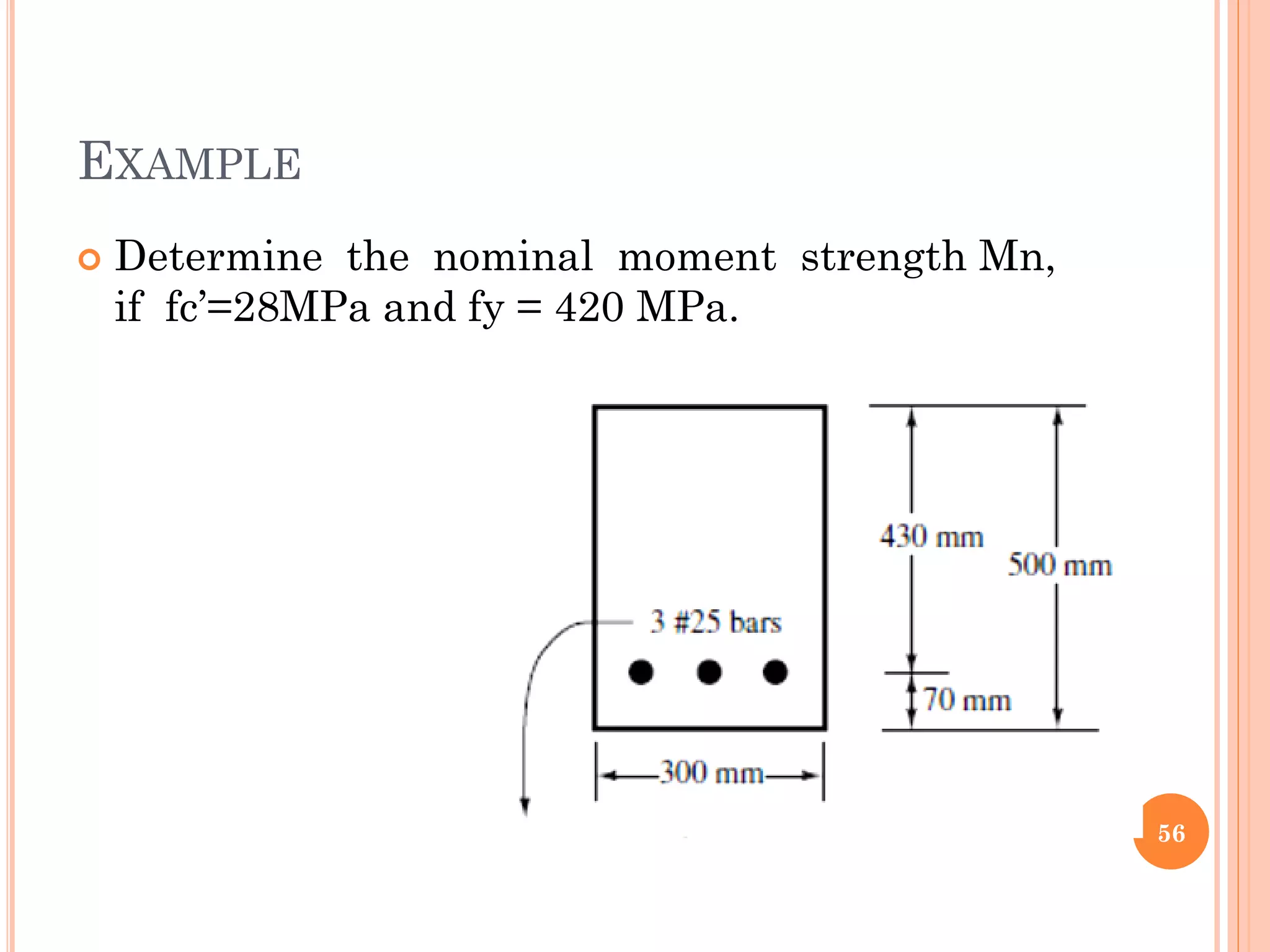
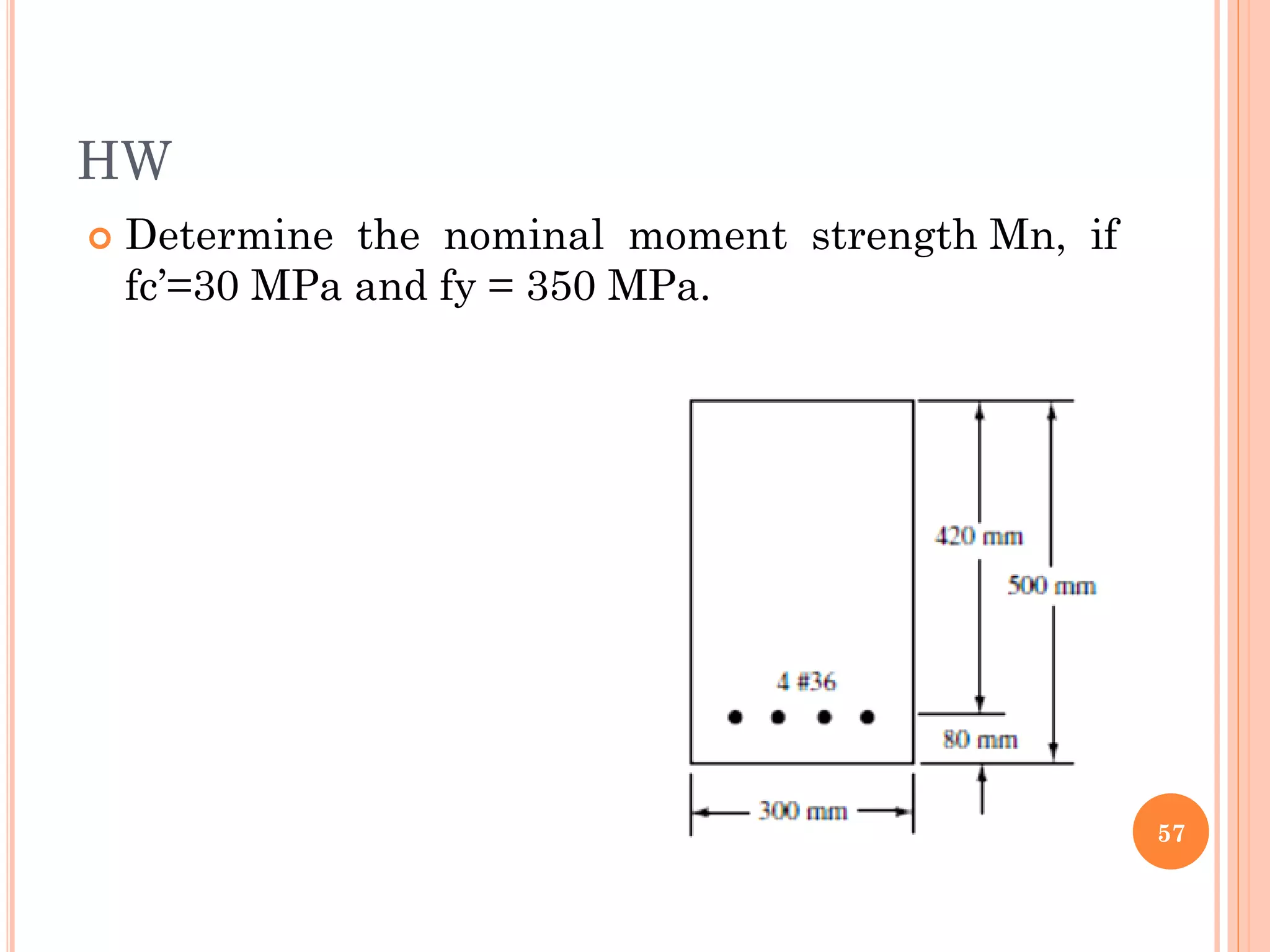
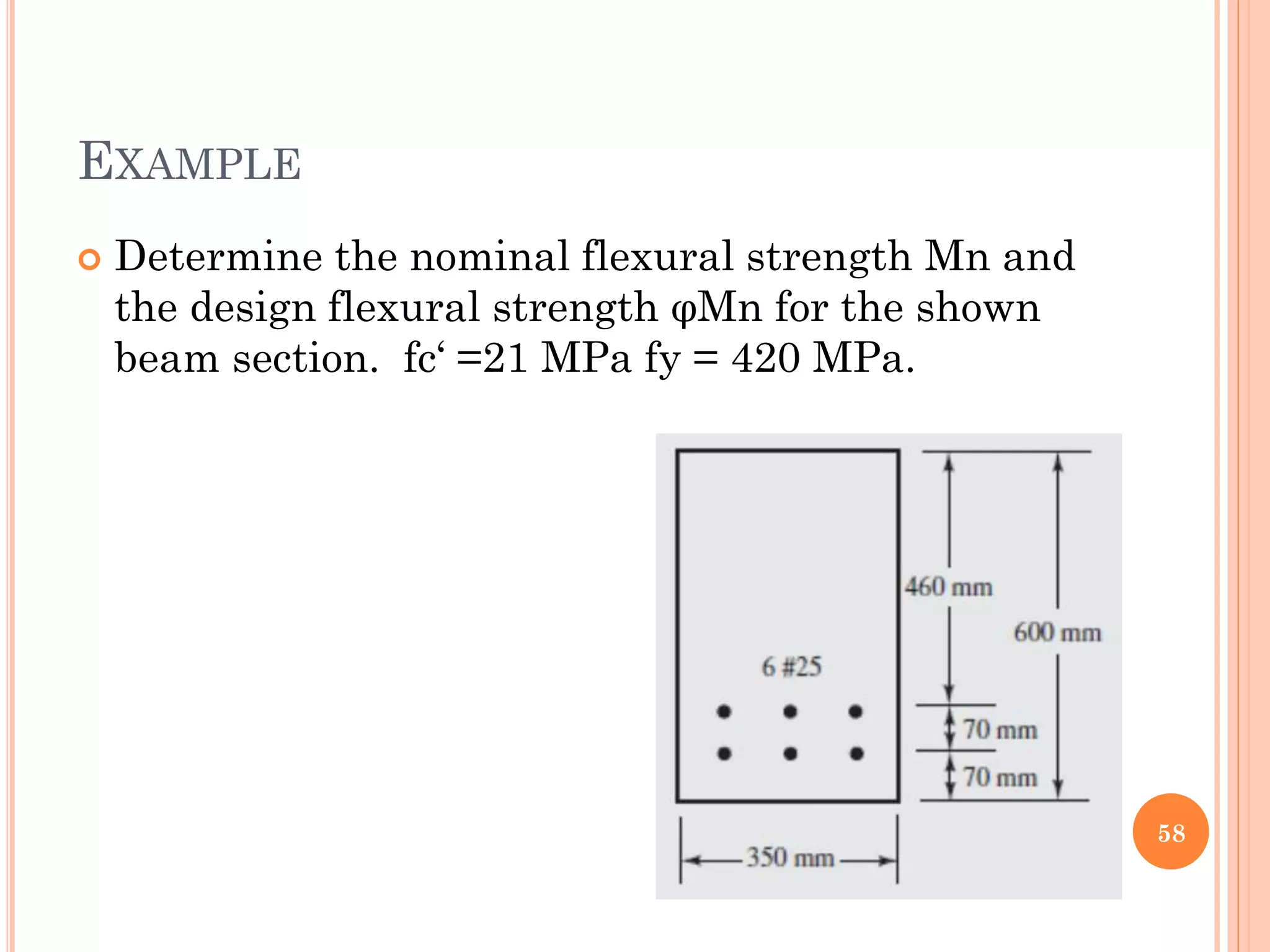
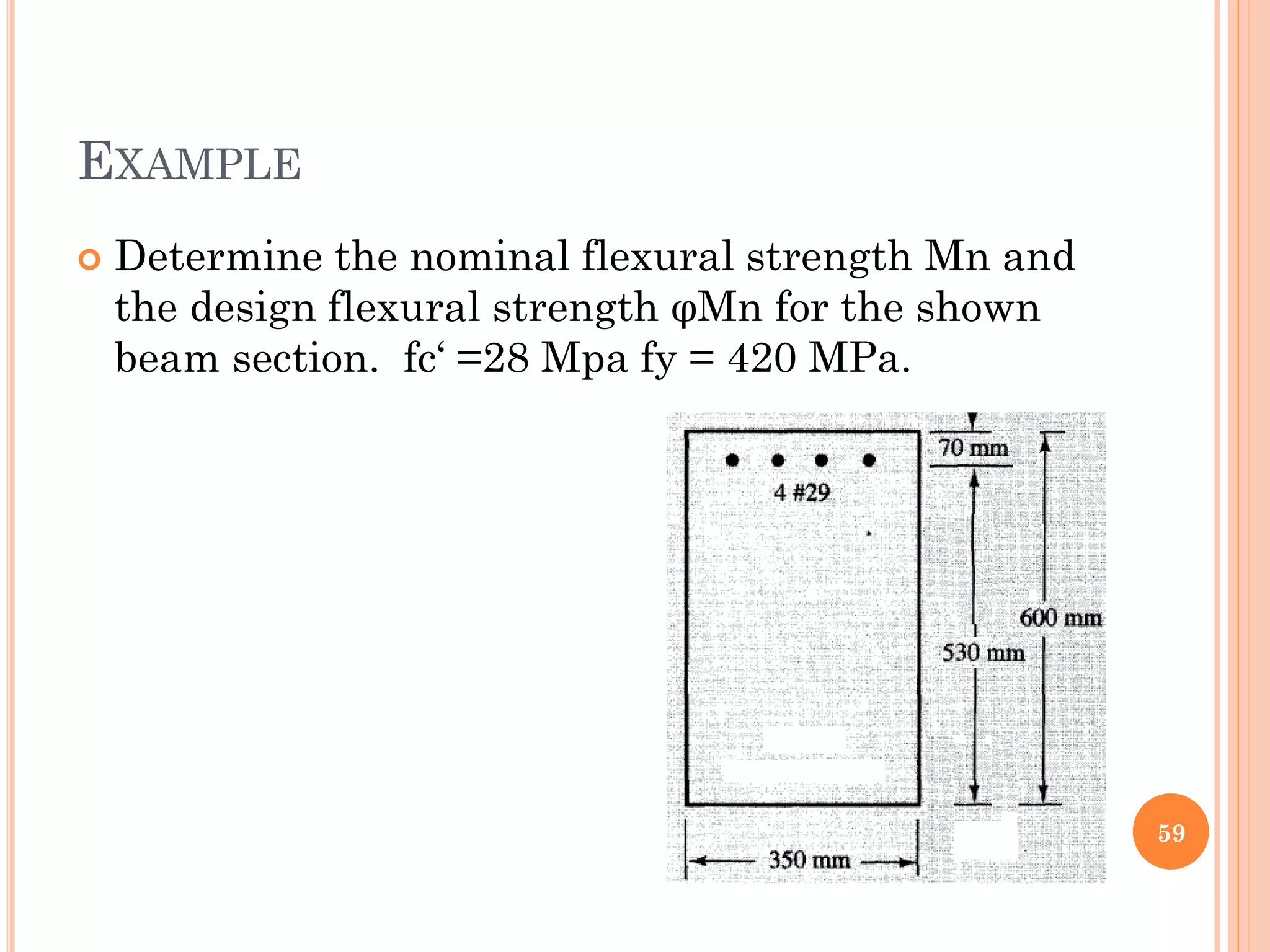
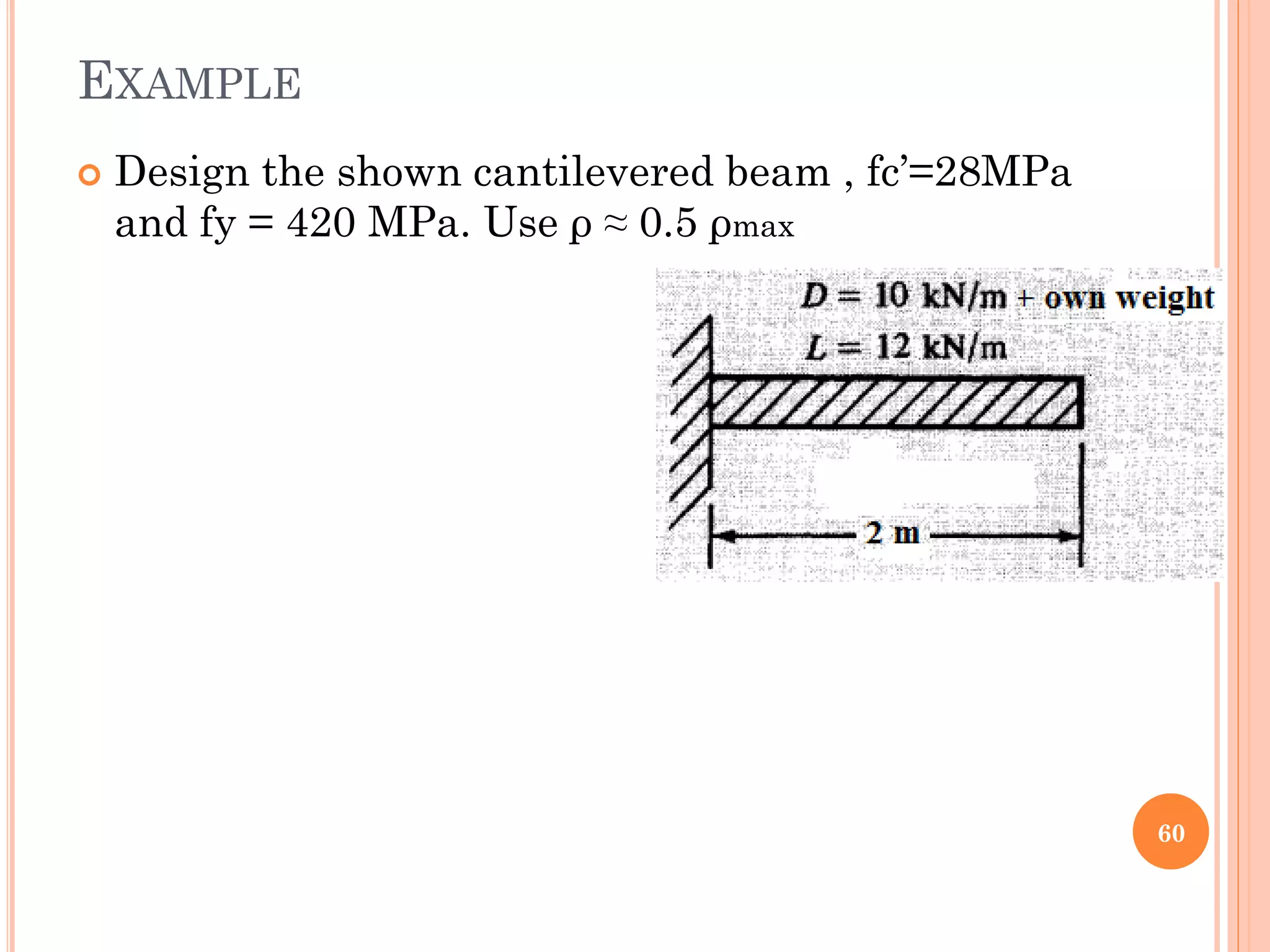
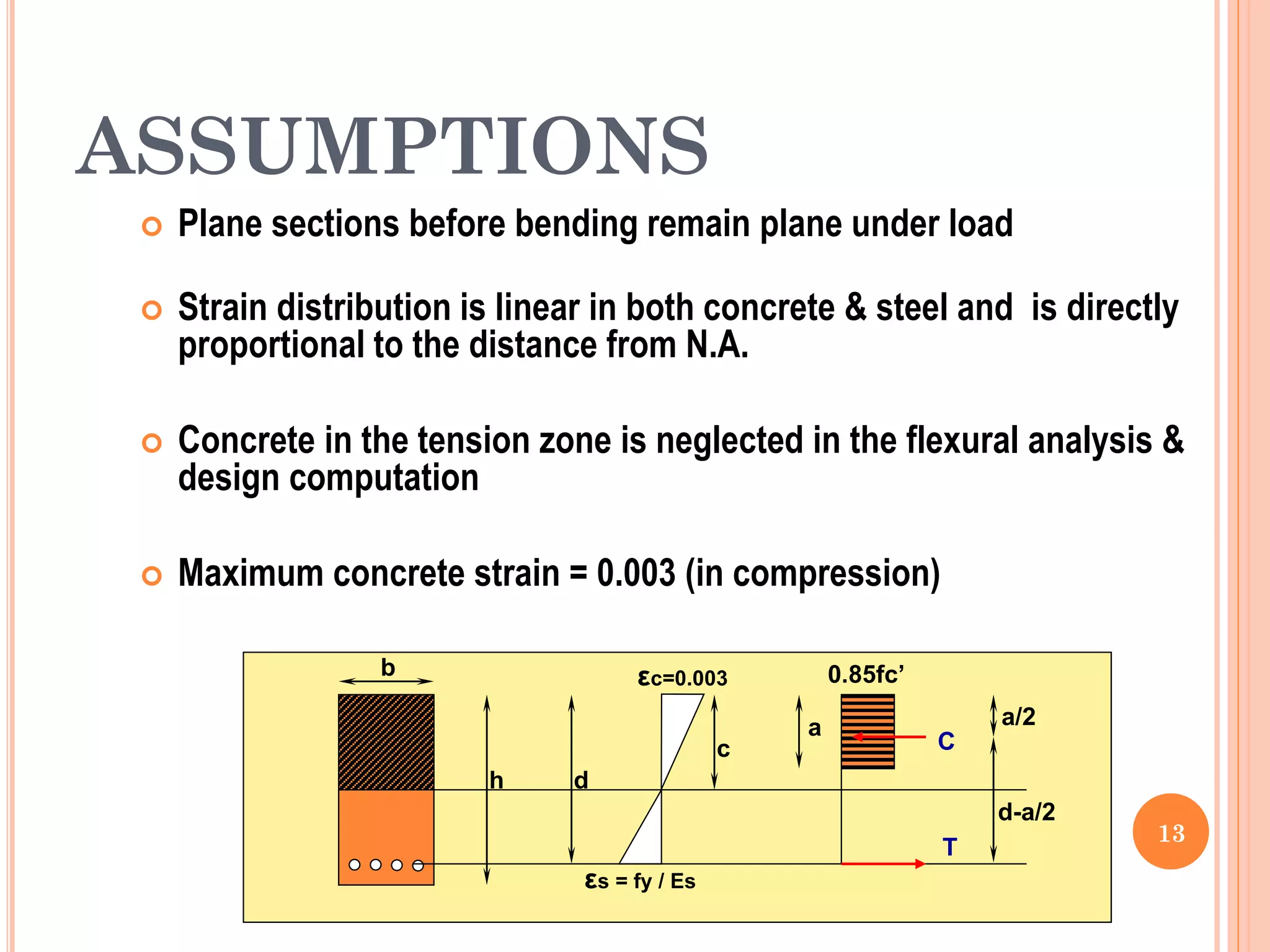
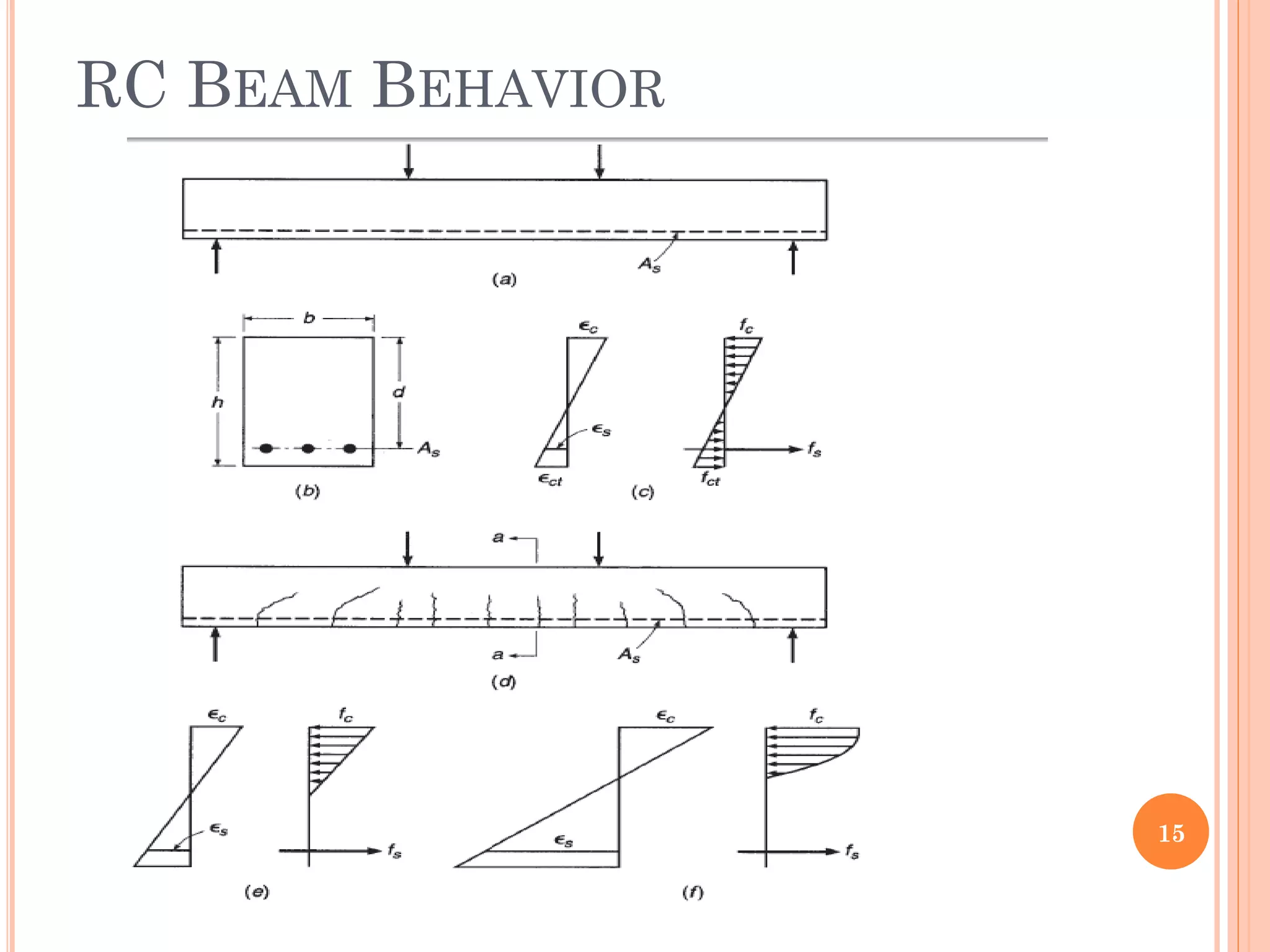
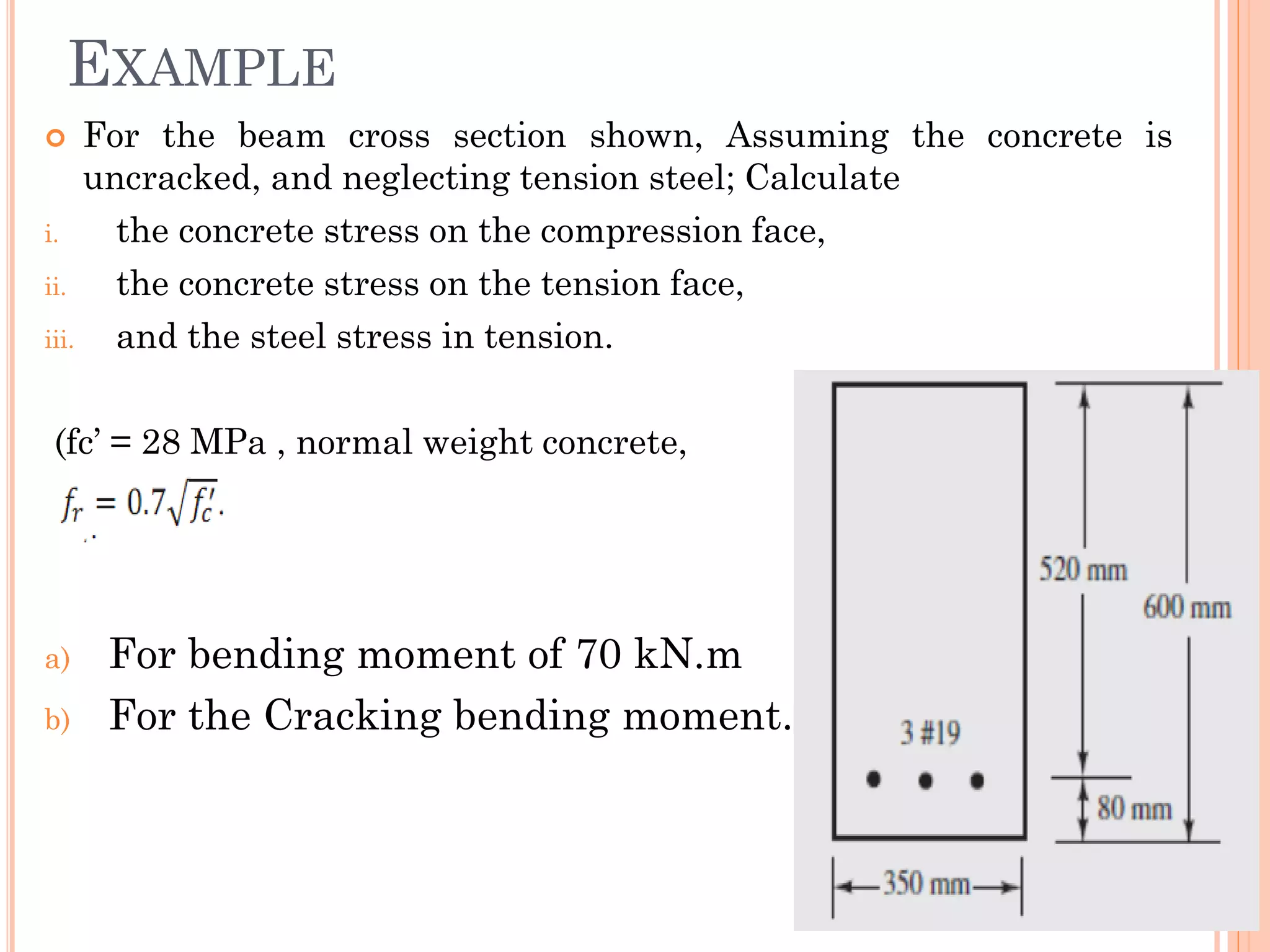
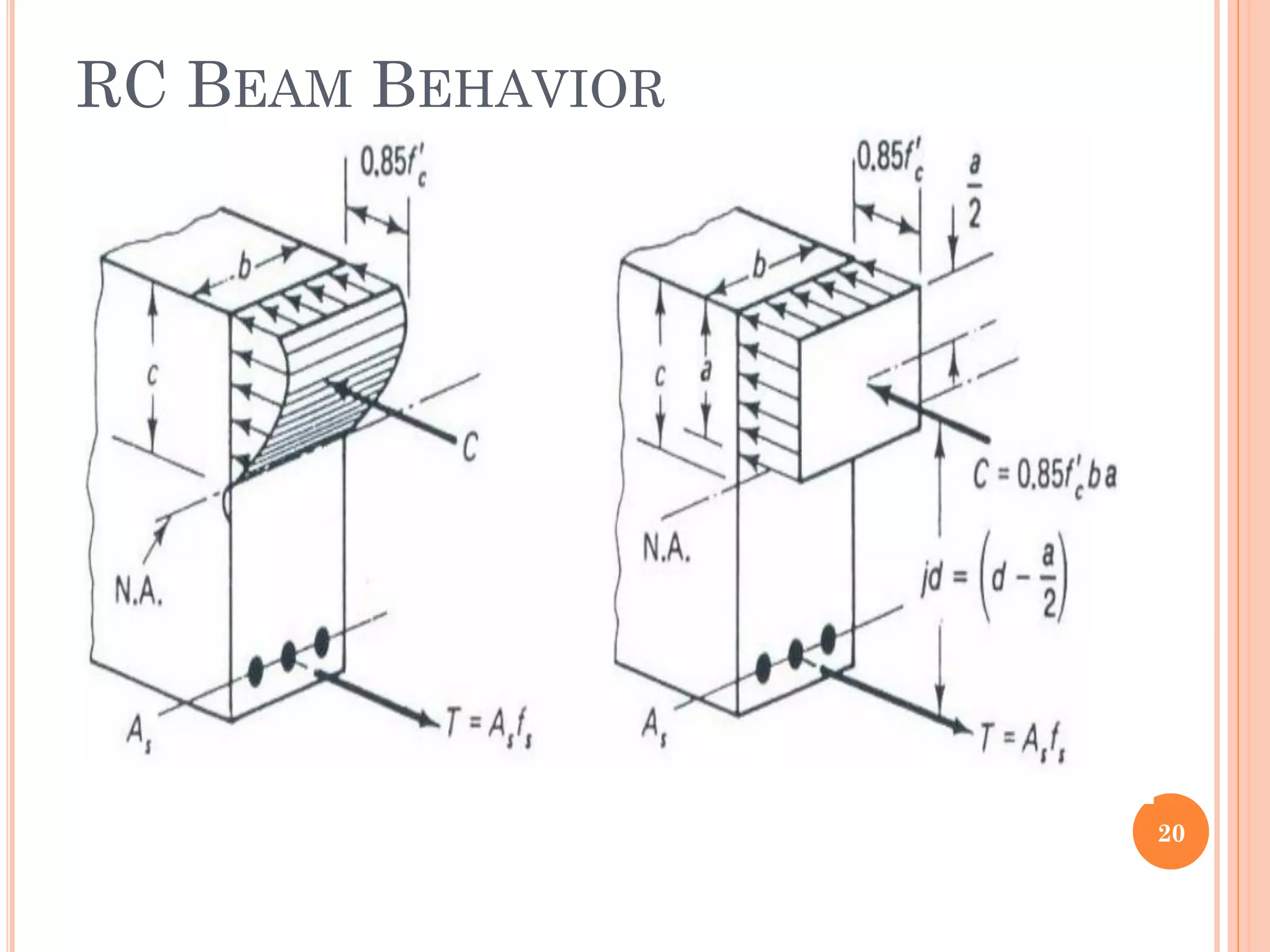
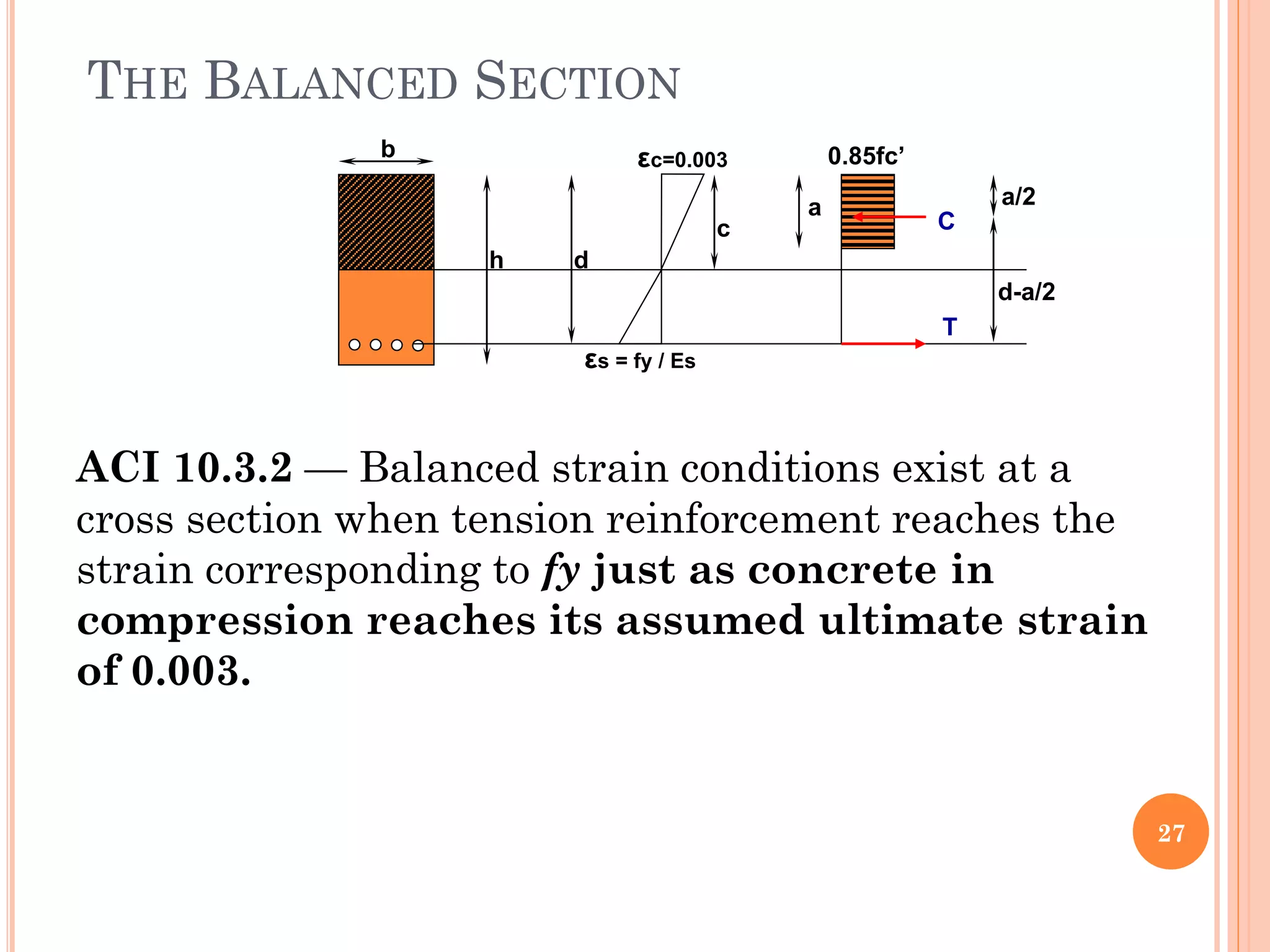
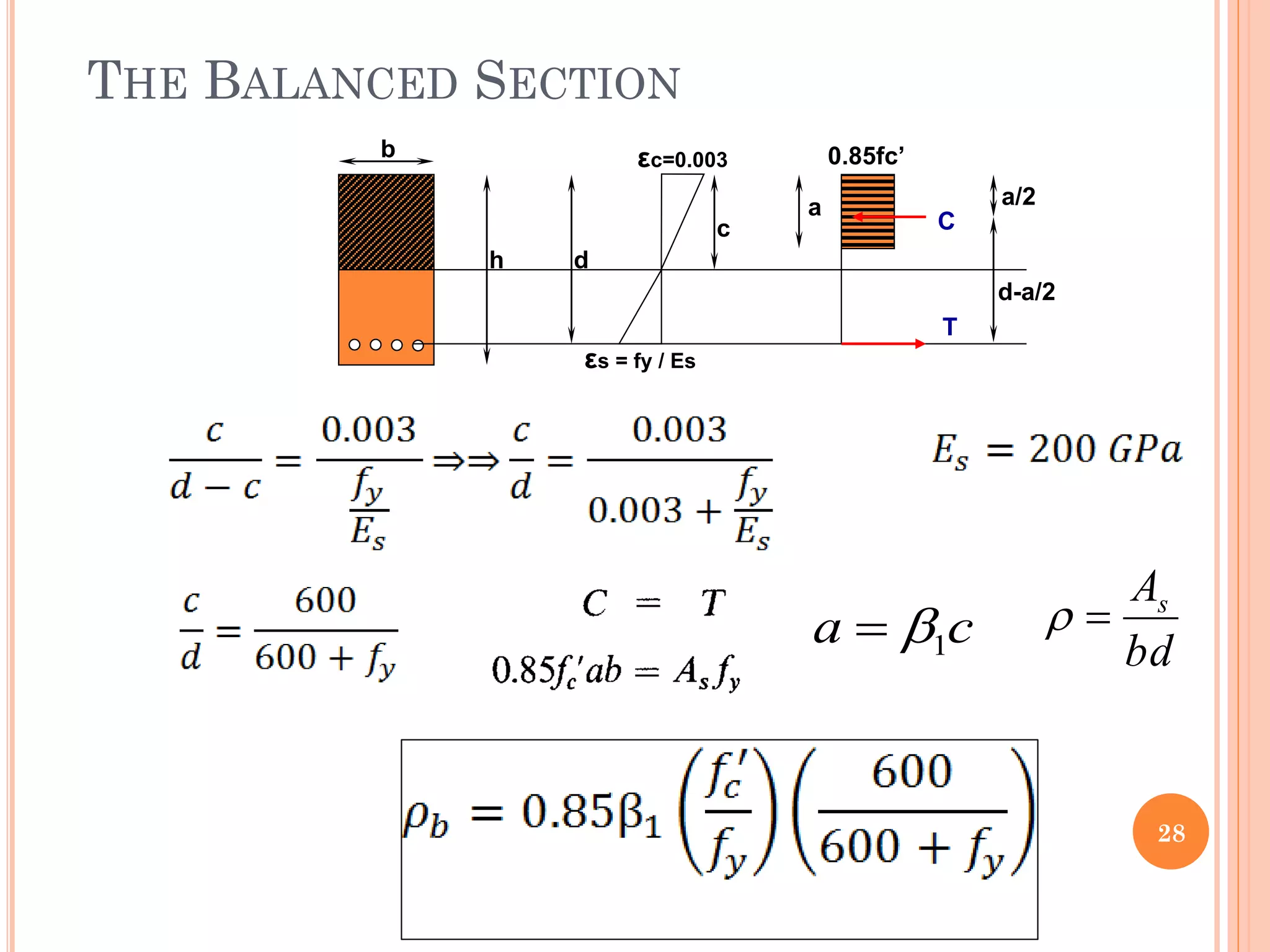
1) The document discusses the flexural analysis and design of reinforced concrete beams. It covers typical beam behavior, stress calculations, flexural equations, and examples of determining nominal moment capacity. 2) Key aspects reviewed include the assumptions in flexural analysis, cracking moment calculations, strain distributions, balanced sections, and code limits on minimum and maximum steel ratios. 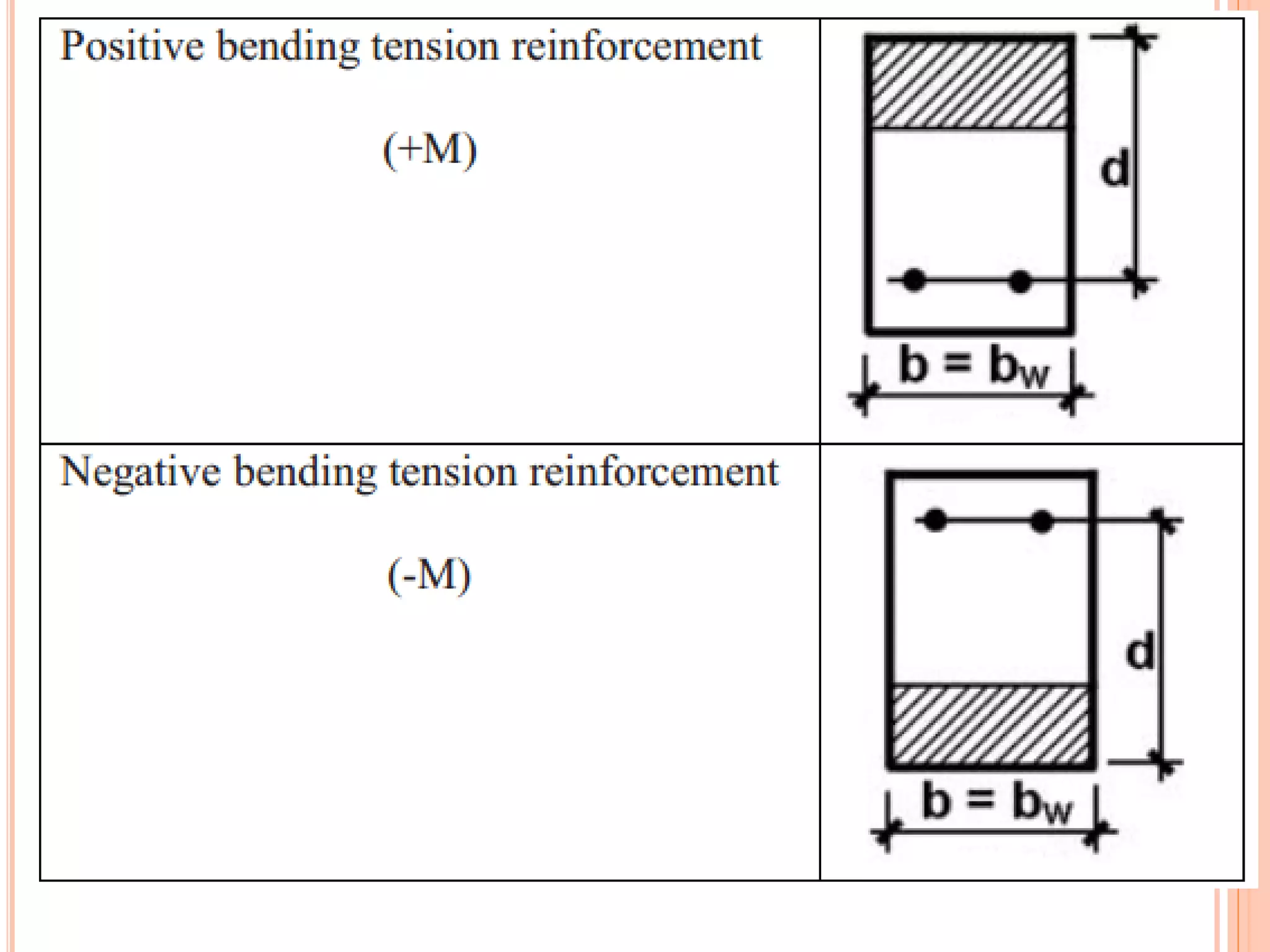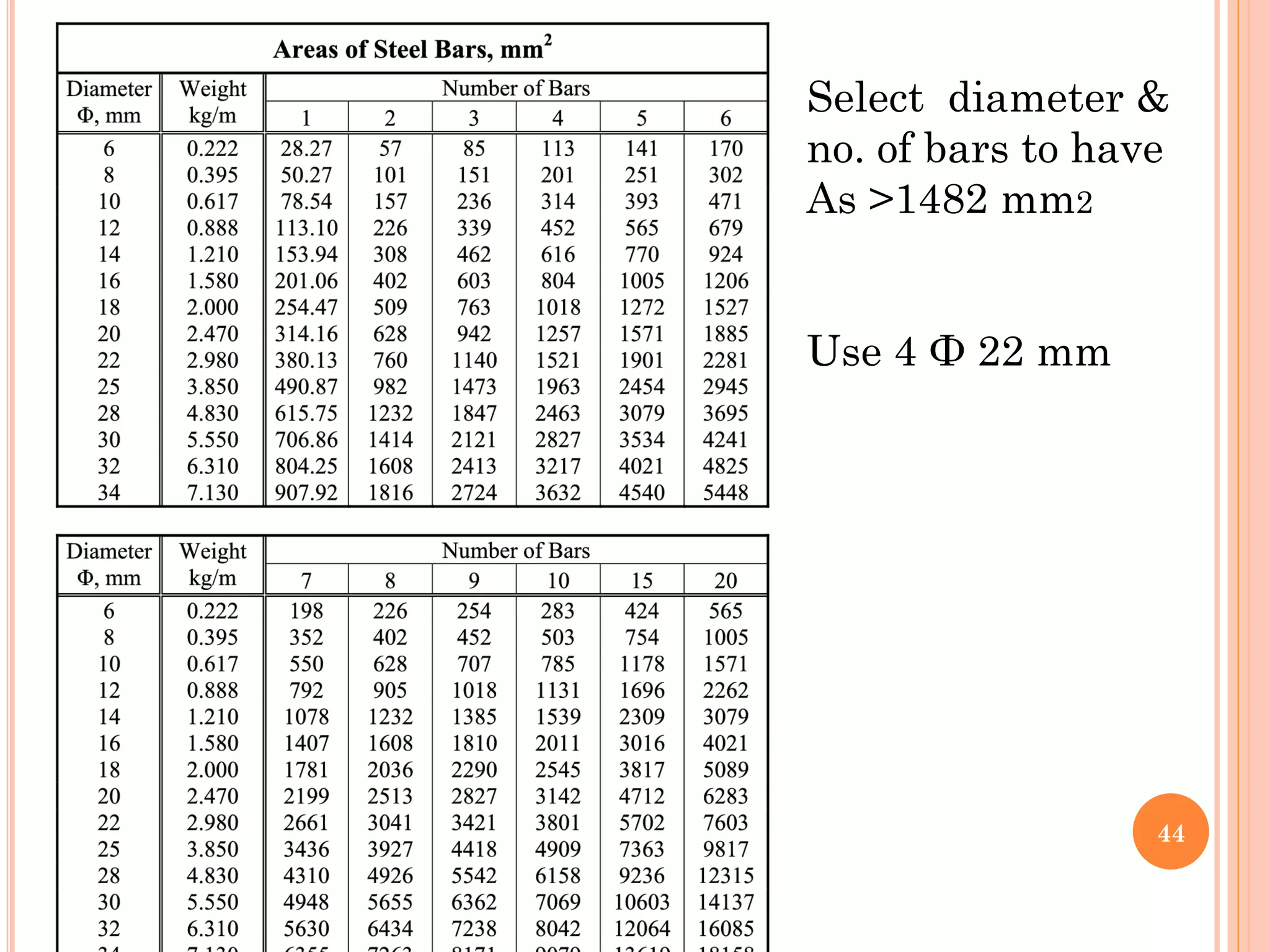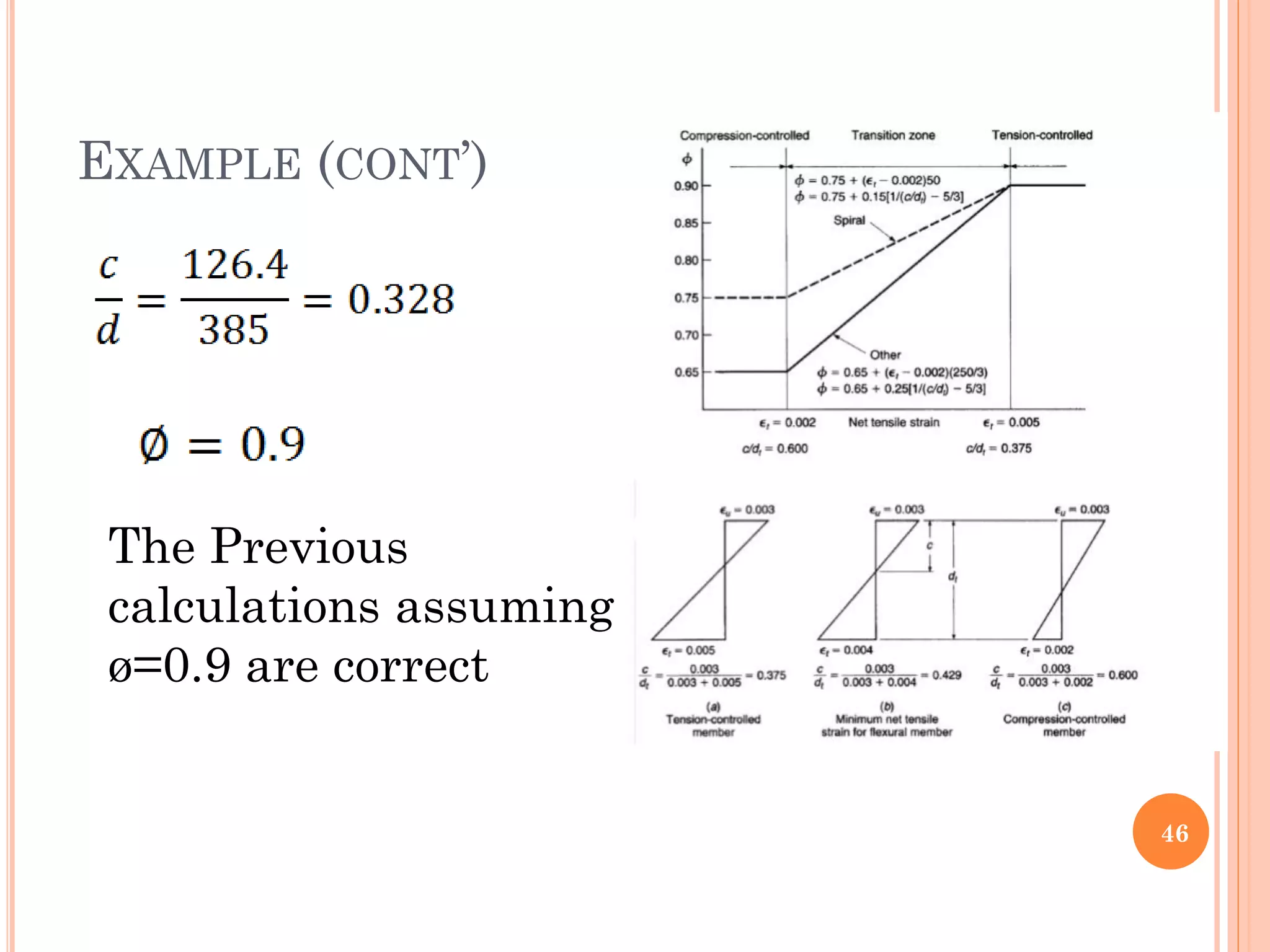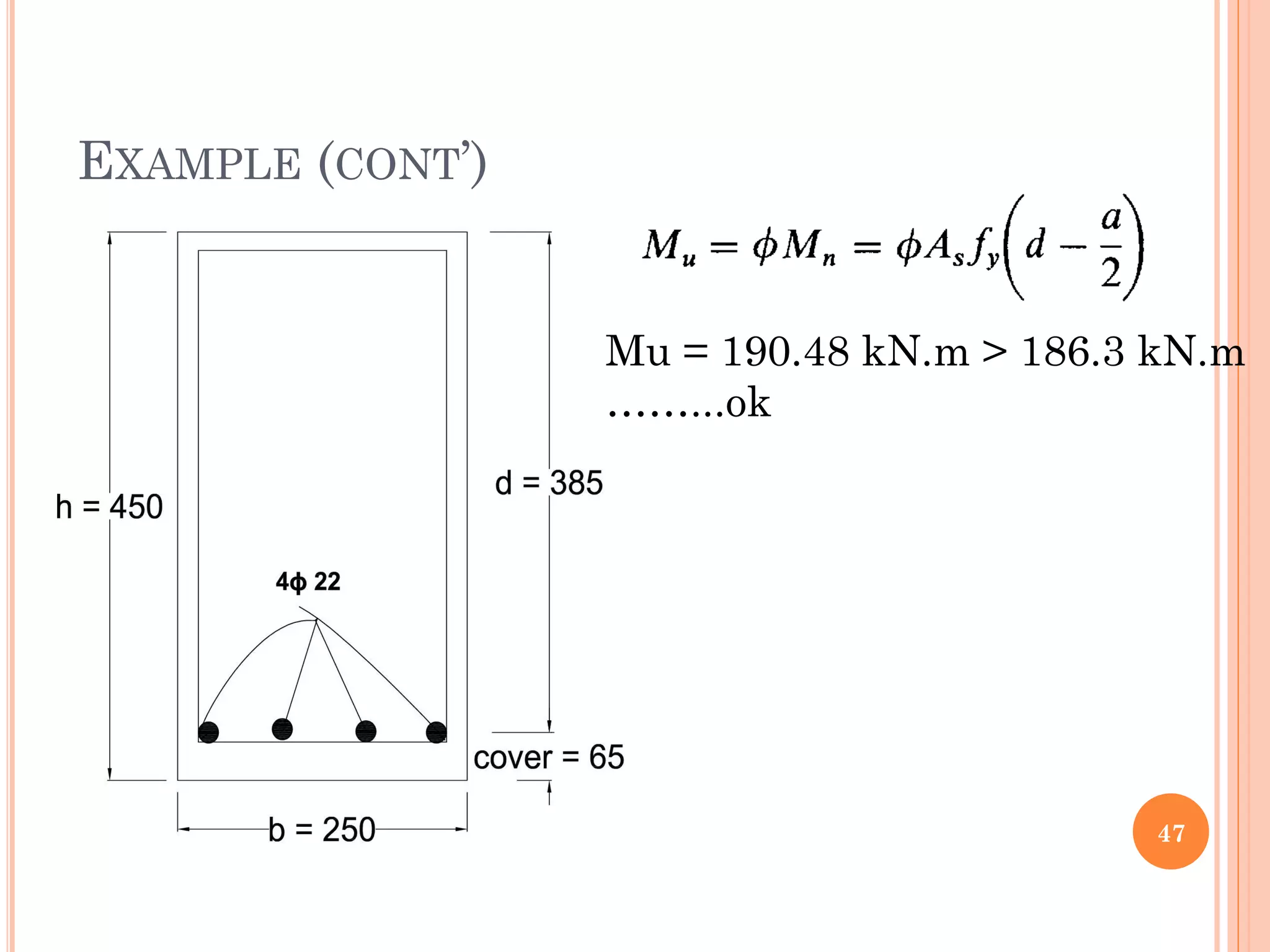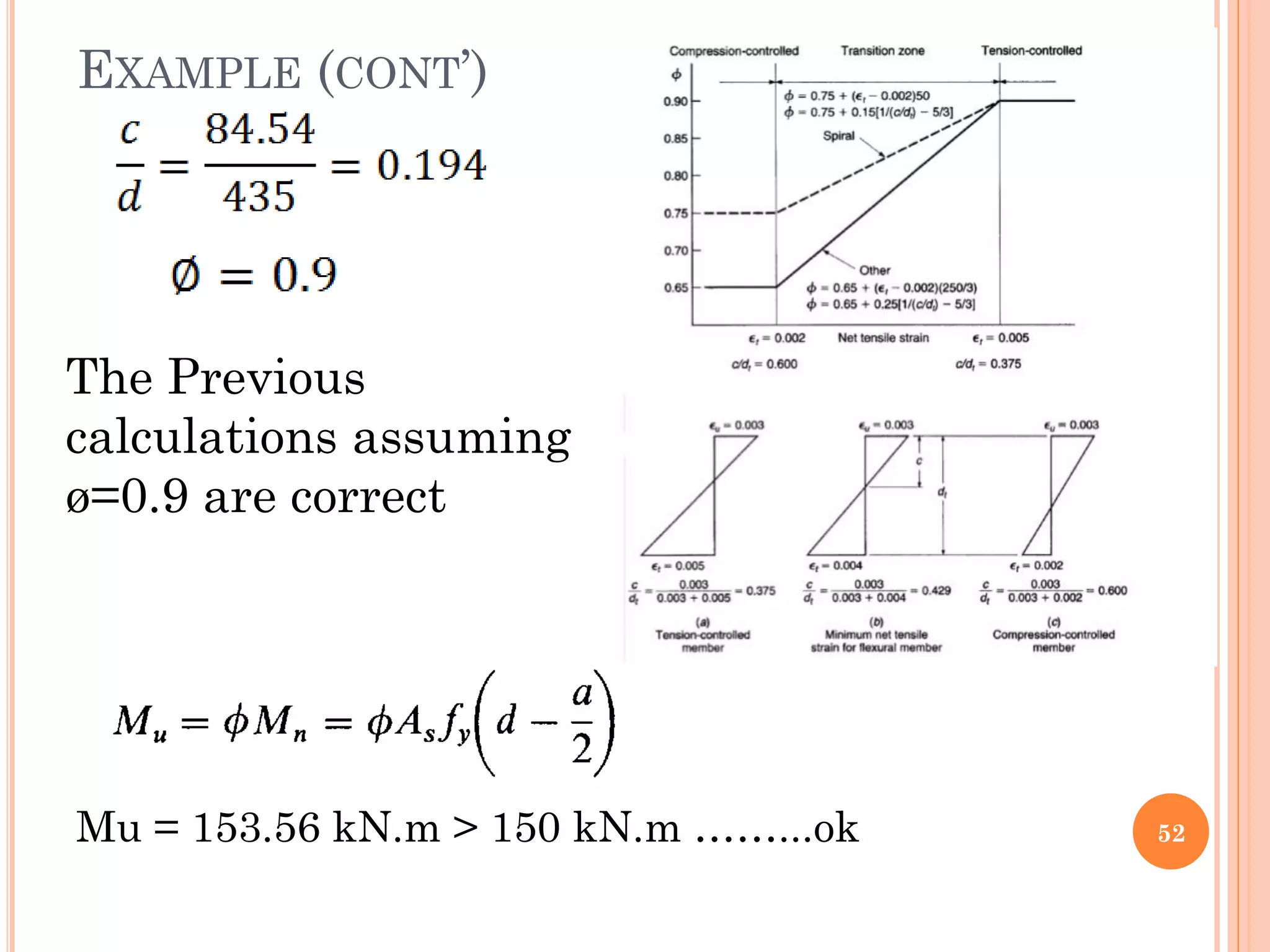3) Practical considerations for concrete dimensions and reinforcement spacing are also addressed. Examples show how to calculate nominal moment strength and design flexural strength for given beam cross-sections.

1. REINFORCED CONCRETE (1)
(CE411)
Chapter 3-a
Flexural Analysis and Design of
Beams
Instructor:
Eng. Abdallah Odeibat
Civil Engineer, Structures , M.Sc.
1

2. INTRODUCTION
2

3. 3

4. 4

5. 5

6. TYPICAL SINGLY REINFORCED CONCRETE
RECTANGULAR BEAM
6

7. 7

8. 8

9. INTRODUCTION
9

10. DEFINITIONS
10

11. FLEXURAL STRESS
11

12. FLEXURAL STRESS
12
The beam is a structural member used
to support the internal moments and
shears. It would be called a beam-
column if a compressive force existed.
C = T
M = C*(jd)
= T*(jd)

13. ASSUMPTIONS
 Plane sections before bending remain plane under load
 Strain distribution is linear in both concrete & steel and is directly
proportional to the distance from N.A.
 Concrete in the tension zone is neglected in the flexural analysis &
design computation
 Maximum concrete strain = 0.003 (in compression)
13
εc=0.003
εs = fy / Es
h d
c
0.85fc’
a a/2
d-a/2
b
C
T

14. RC BEAM BEHAVIOR
 Assume that a small transverse load is placed on a
concrete beam with tensile reinforcing and that load is
gradually increased in magnitude until the beam
fails. As this happen the beam will go through three
behavior stages before collapse:
1. Uncracked Concrete Stage
2. Concrete Cracked–Elastic Stresses Stage
3. Beam Failure—Ultimate-Strength Stage
14

15. RC BEAM BEHAVIOR
15

16. 16
Cracking Moment

17.  For the beam cross section shown, Assuming the concrete is
uncracked, and neglecting tension steel; Calculate
i. the concrete stress on the compression face,
ii. the concrete stress on the tension face,
iii. and the steel stress in tension.
(fc’ = 28 MPa , normal weight concrete,
a) For bending moment of 70 kN.m
b) For the Cracking bending moment.
EXAMPLE
17

18. SOLUTION
 a)
18

19. 19
 b)

20. RC BEAM BEHAVIOR
20

21. RC BEAM BEHAVIOR
21
c
a 1



22. FLEXURE EQUATIONS
22
bd
As



23. 23
Strain

24. EXAMPLE
 Determine nominal moment capacity and design
(ultimate) moment capacity of R.C. rectangular
section.
Given: fc’ = 35 MPa
fy= 400 MPa
b = 350 mm
d = 550 mm
As = 4 ø 32; Area = 3217 mm2
24

25. SOLUTION
 Assume stress in steel reaches yield stress :
T=C
3217 (400) = 0.85 (35)(350)x a
Get a= 123.6 mm a/2 = 61.8 mm
Mn = 1286.8 (550-61.8) x 10-3 = 628.216 kN.m
Check if steel has yielded
β1 = 0.85 – (35-28)(0.05)/7=0.8
c = a/ β1 = 123.6/0.8 =154.5 mm
25

26. SOLUTION (CONT’)
 From strain distribution,
εs = 0.00768 > εy
Knowing that εy = fy / Es = 400 /200,000 =0.002
So assumption is acceptable;
Mn = 628.216 kN.m
Mu = øMn = 0.9(628.216) kN.m = 565.4 kN.m
26

27. THE BALANCED SECTION
27
εc=0.003
εs = fy / Es
h d
c
0.85fc’
a a/2
d-a/2
b
C
T
ACI 10.3.2 — Balanced strain conditions exist at a
cross section when tension reinforcement reaches the
strain corresponding to fy just as concrete in
compression reaches its assumed ultimate strain
of 0.003.

28. THE BALANCED SECTION
28
εc=0.003
εs = fy / Es
h d
c
0.85fc’
a a/2
d-a/2
b
C
T
c
a 1

 bd
As



29. MAXIMUM RATIO OF STEEL
(FOR ϵT =0.004, Φ = 0.817)
 ACI code limits the maximum ratio of steel
 If we use compression block depth,
29

30.  If (under-reinforced) (ductile failure)
30

31.  If (over-reinforced) (brittle failure)
In this case, we have 2 unknowns : fs , a
Solution of this equation will be done by
trial and error; or by quadratic
equation in term of c.
 ACI code recommends to use ρmax .
31

32. TENSION CONTROLLED SECTION
(FOR ϵT =0.005, Φ = 0.9)
 ACI code limits the maximum ratio of steel
 If we use compression block depth,
32

33. EXAMPLE
 Determine ultimate Moment Capacity of
R.C. rectangular section.
Given: fc’ = 25 MPa
fy= 280 MPa
b = 200 mm
d = 300 mm
If
a) As = 4 ø 18 mm;
b) As = 4 ø 22 mm(HW)
c) As = 4 ø 25 mm
d) As = 4 ø 28 mm(HW)
33

34. 34

35. 35

36. 36

37. MINIMUM RATIO OF STEEL
37

38. CONCRETE DIMENSIONS AND REINFORCEMENT
DESIGN
38
d
b
As .
.



39. EXAMPLE
 Find the concrete cross section and the
steel area required for a simply supported
rectangular beam with a span of 4.5 m
that to carry a service dead load of
20kN/m and service live load of 31kN/m ,
material strength are fc’ = 28MPa and
fy=420 MPa ?
 Solution:
39

40. EXAMPLE (CONT’)
 If we want to minimize the concrete section, it is
desirable to use
40

41. EXAMPLE (CONT’)
41
 Use b = 250 mm then d =342 mm
or
Use b = 200 mm then d = 383mm
Selection of any alternative
is the designer option

42. EXAMPLE (CONT’)
42
 If we select b = 250 mm and d =342 mm
 Assuming 65 mm concrete cover
 h= d+cover = 342+65=407 mm
 h and b are often rounded up to the
nearest multiple of 50 mm.
 Use h=450 mm
 The actual d = h – cover = 450-65=385 mm

43. EXAMPLE (CONT’)
 Required As based on the selected dimensions :
43
For Mu = 186.3 *10^6 N.mm, fc’ = 28 MPa , fy = 420 MPa
b= 250 mm , d= 385 mm , Ф =0.9 (to be checked)
ρ = 0.015398 , check
As = ρ b d =1482 mm2

44. 44
Select diameter &
no. of bars to have
As >1482 mm2
Use 4 Ф 22 mm

45. EXAMPLE (CONT’)
 Use 4 Ф 22 mm ….As provided = 1521 mm2
 Check spacing of bars : it is required that :
…………………………………………………………….
45
107.4 mm
=107.4 mm / 0.85 =126.4 mm

46. EXAMPLE (CONT’)
46
The Previous
calculations assuming
ø=0.9 are correct

47. EXAMPLE (CONT’)
47
Mu = 190.48 kN.m > 186.3 kN.m
……...ok

48. EXAMPLE (CONT’)
 A more economical and practical design can be
obtained using
HW : Redesign the previous
beam using
48

49. EXAMPLE
 For concrete section of b= 250 mm, d=435 mm
and h=500mm, find the steel area required to
resist Mu = 150 kN.m, , material properties are
fc’ = 28MPa and fy=420 MPa ?
Solution:
.
49

50. EXAMPLE (CONT’)
50
ρ = 0.00913 , check
As = ρ b d = 992.6 mm2
For Mu = 150 *10^6 N.mm, fc’ = 28 MPa , fy = 420 MPa
b= 250 mm , d= 435 mm , Ф =0.9 (to be checked)

51. EXAMPLE (CONT’)
51
Select diameter & no. of bars to have As >992.6mm2
Use 4 Ф 18mm …..As provided =1018 mm2
…………………………………………………………….
71.86 mm
= 71.86 mm / 0.85 =84.54 mm

52. EXAMPLE (CONT’)
52
The Previous
calculations assuming
ø=0.9 are correct
Mu = 153.56 kN.m > 150 kN.m ……...ok

53. PRACTICAL CONSIDERATION (COVER)
53

54. PRACTICAL CONSIDERATION (DIMENSIONING)
 h and b are almost rounded up to the nearest
multiple of 25 mm, and often to the next multiple
of 50 mm.
 b and d are economically and practically chosen
with
d = (2 to 3)*b.
54

55. PRACTICAL CONSIDERATION (BAR SPACING)
55

56. EXAMPLE
 Determine the nominal moment strength Mn,
if fc’=28MPa and fy = 420 MPa.
56

57. HW
 Determine the nominal moment strength Mn, if
fc’=30 MPa and fy = 350 MPa.
57

58. EXAMPLE
 Determine the nominal flexural strength Mn and
the design flexural strength φMn for the shown
beam section. fc‘ =21 MPa fy = 420 MPa.
58

59. EXAMPLE
 Determine the nominal flexural strength Mn and
the design flexural strength φMn for the shown
beam section. fc‘ =28 Mpa fy = 420 MPa.
59

60. EXAMPLE
 Design the shown cantilevered beam , fc’=28MPa
and fy = 420 MPa. Use ρ ≈ 0.5 ρmax
60