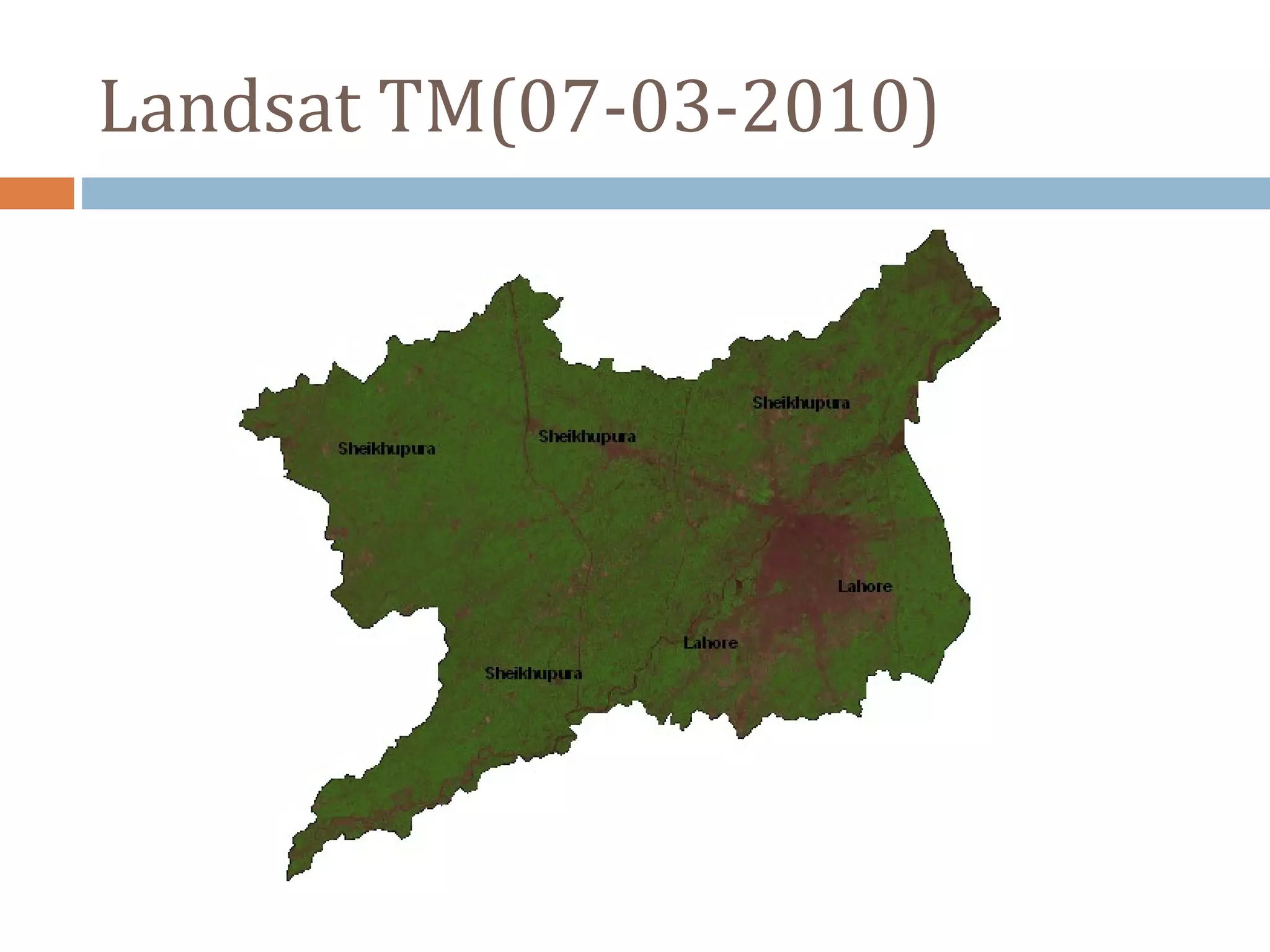
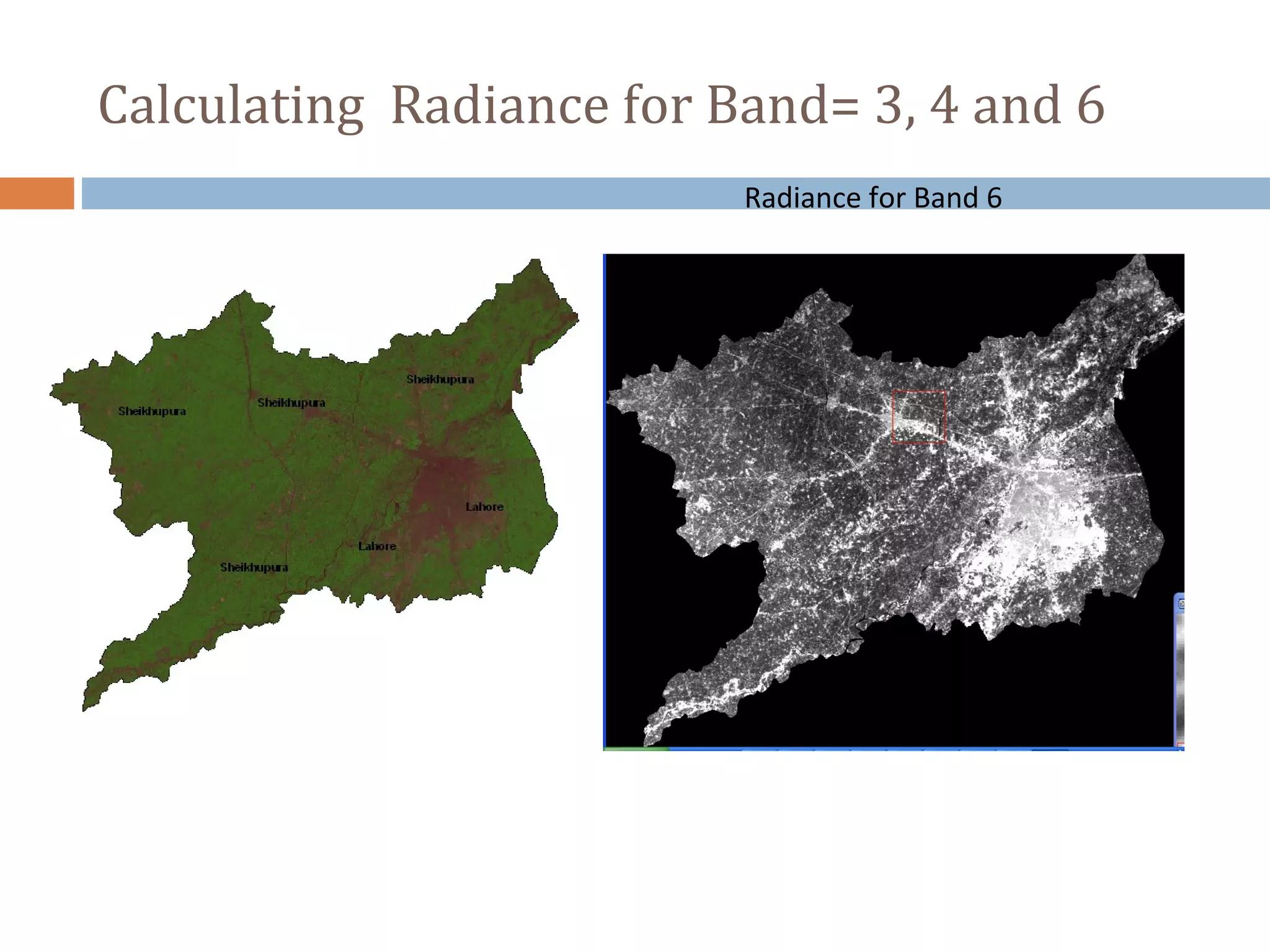
This document describes using Landsat TM data to calculate the Normalized Difference Vegetation Index (NDVI), land surface emissivity (LSE), and land surface temperature (LST). It outlines the steps to calculate slope and radiance for bands 3, 4, and 6, then determine brightness temperature. Next, it explains how to derive LSE from NDVI and use this to calculate surface temperature using Planck's law. The goal is to study NDVI and LST for the Landsat image from March 7, 2010.





![Calculating Land surface emissivity (LSE)- ε
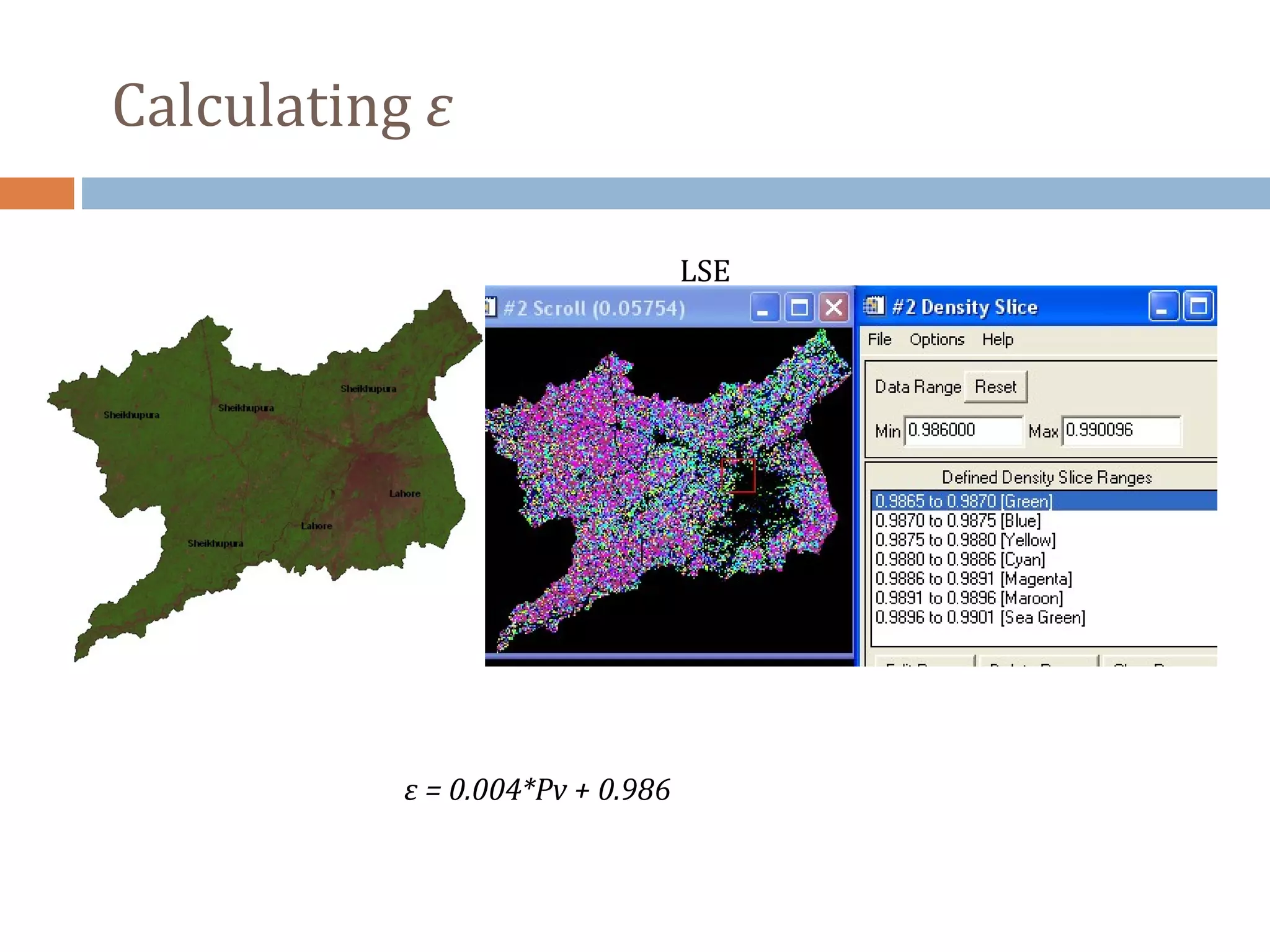
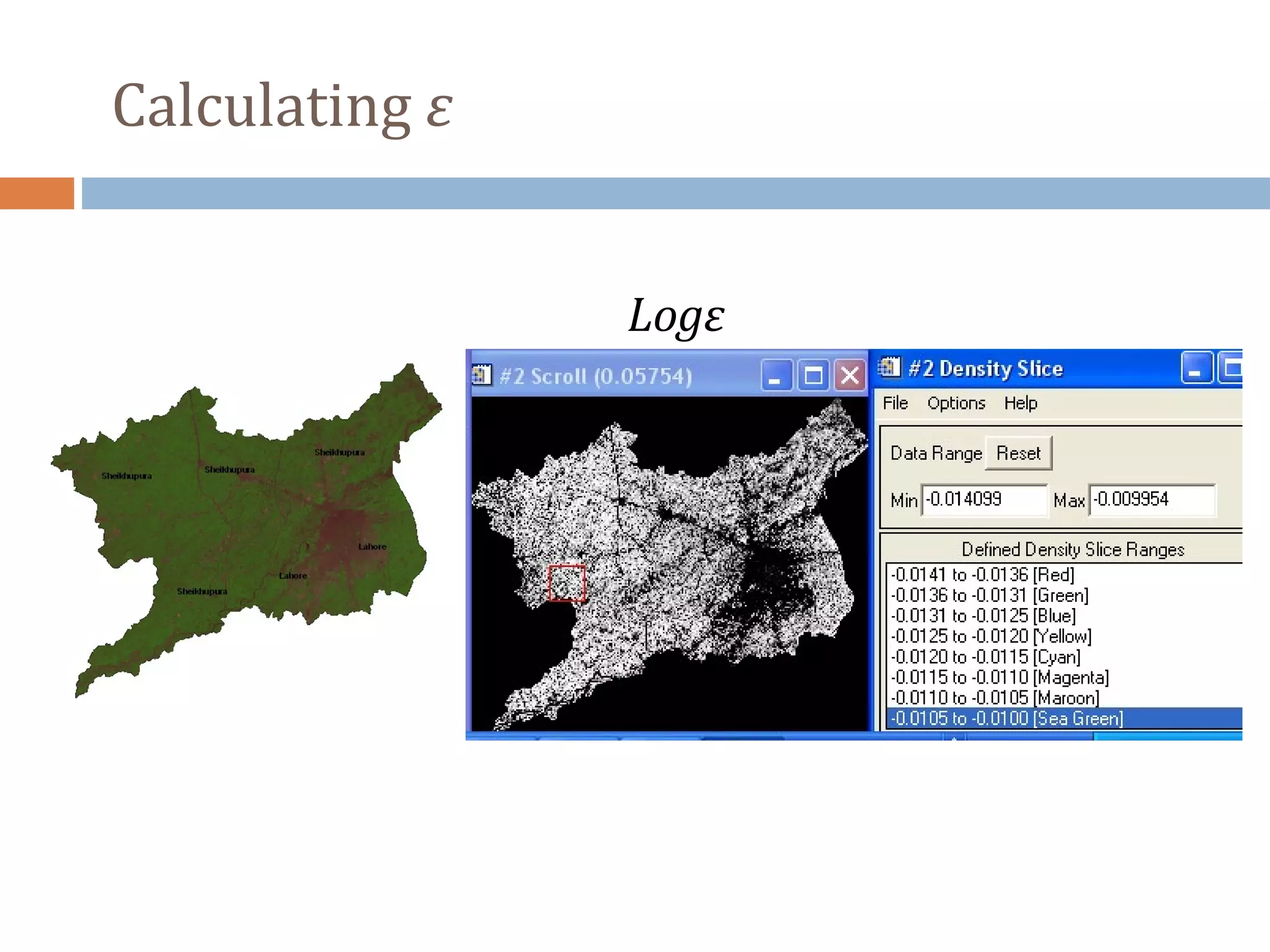
LSE (ε) can be extracted by using NDVI considering
three different cases
Bare ground
Fully vegetated and
Mixture of bare soil and vegetation
For Band 6 of Landsat TM
ε = 0.004*Pv + 0.986
Pv is the proportion of vegetation which is given by
Pv = [(NDVI-NDVImin)/(NDVImax-NDVImin)]2](https://image.slidesharecdn.com/study-of-ndvi-land-surface-temperature-using-landsat-tm-data-140321164427-phpapp01/75/Study-of-ndvi-land-surface-temperature-using-landsat-tm-data-8-2048.jpg)
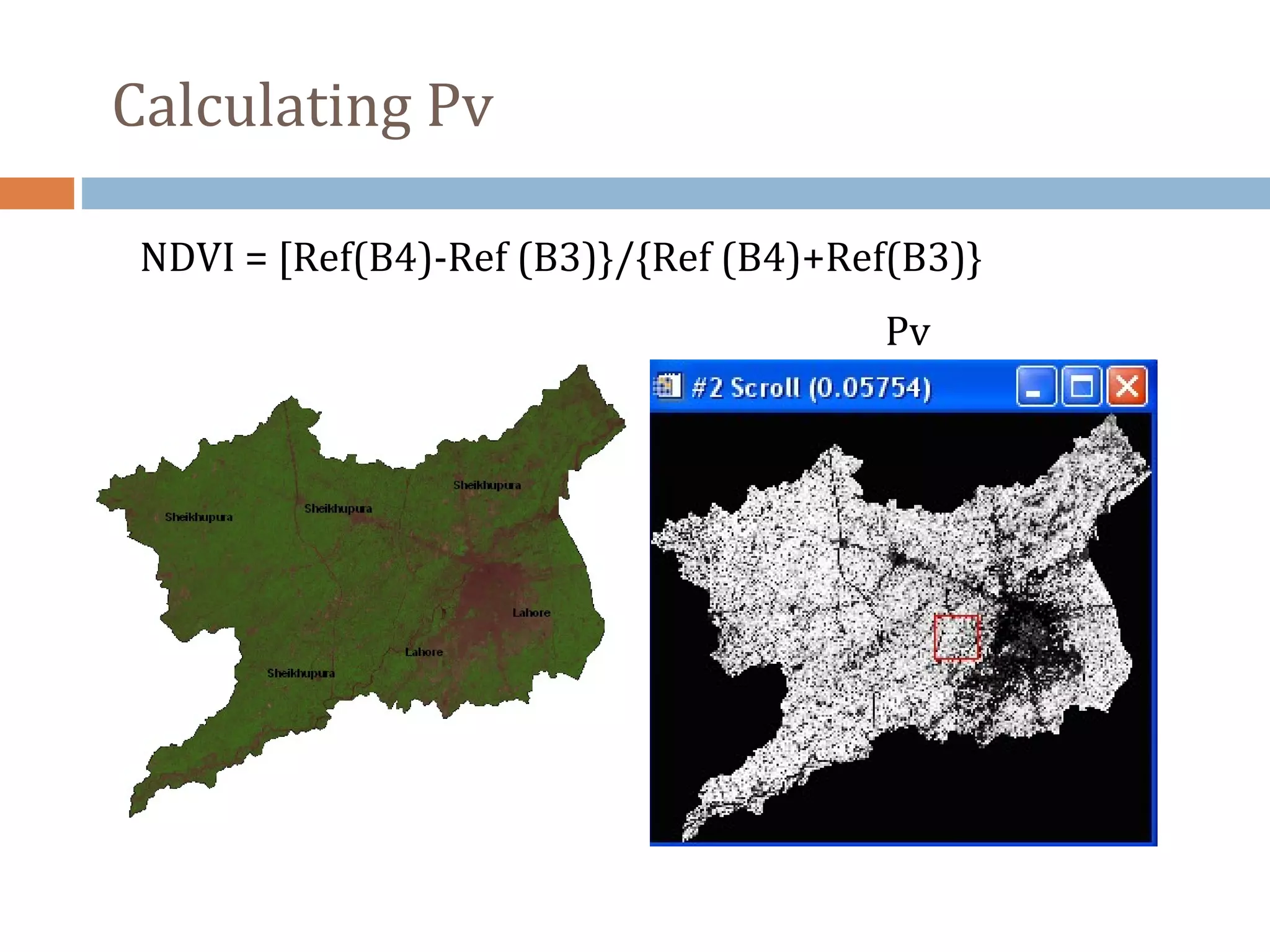
![Pv = [(NDVI-NDVImin)/(NDVImax-NDVImin)]2](https://image.slidesharecdn.com/study-of-ndvi-land-surface-temperature-using-landsat-tm-data-140321164427-phpapp01/75/Study-of-ndvi-land-surface-temperature-using-landsat-tm-data-10-2048.jpg)