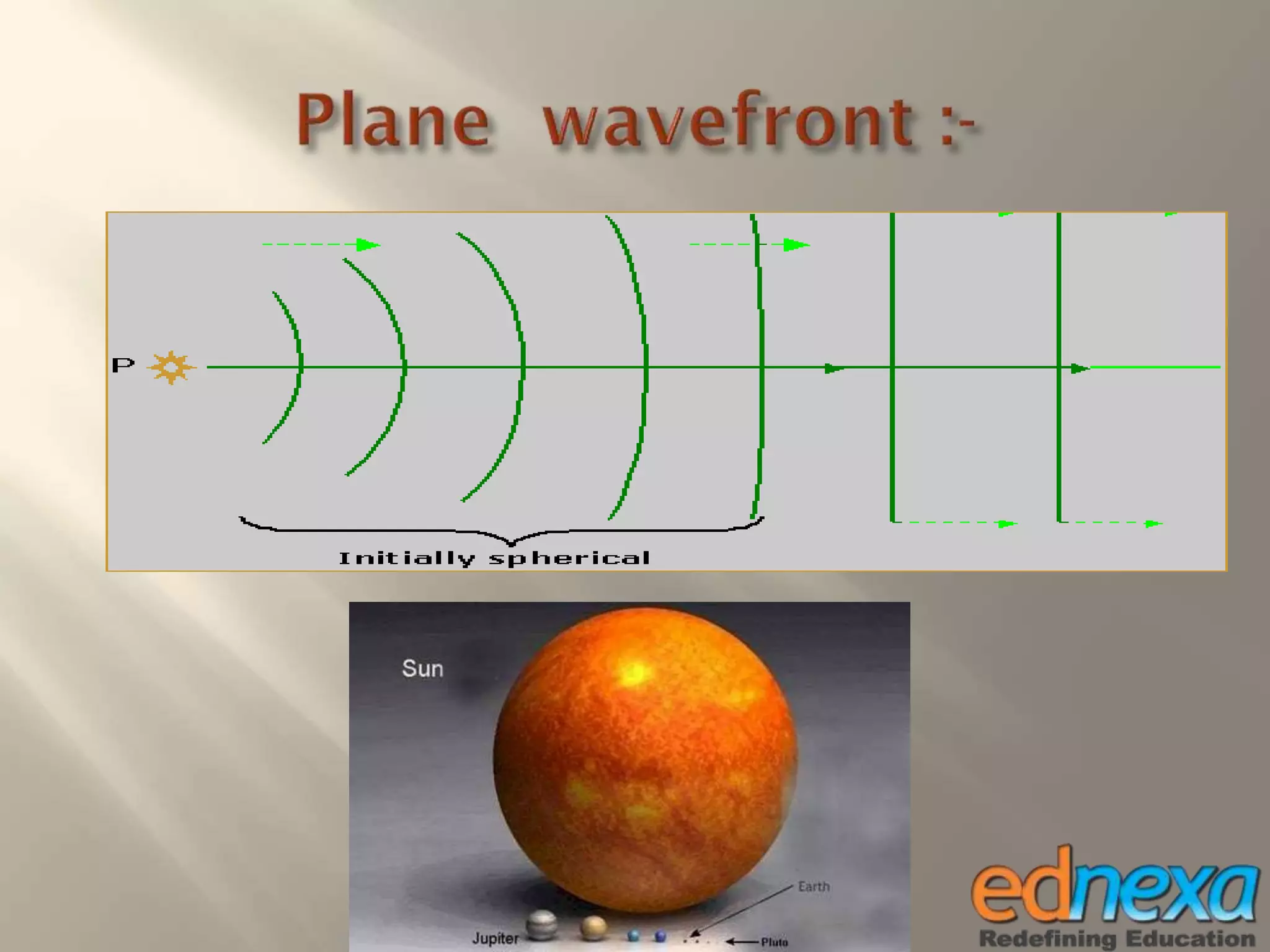
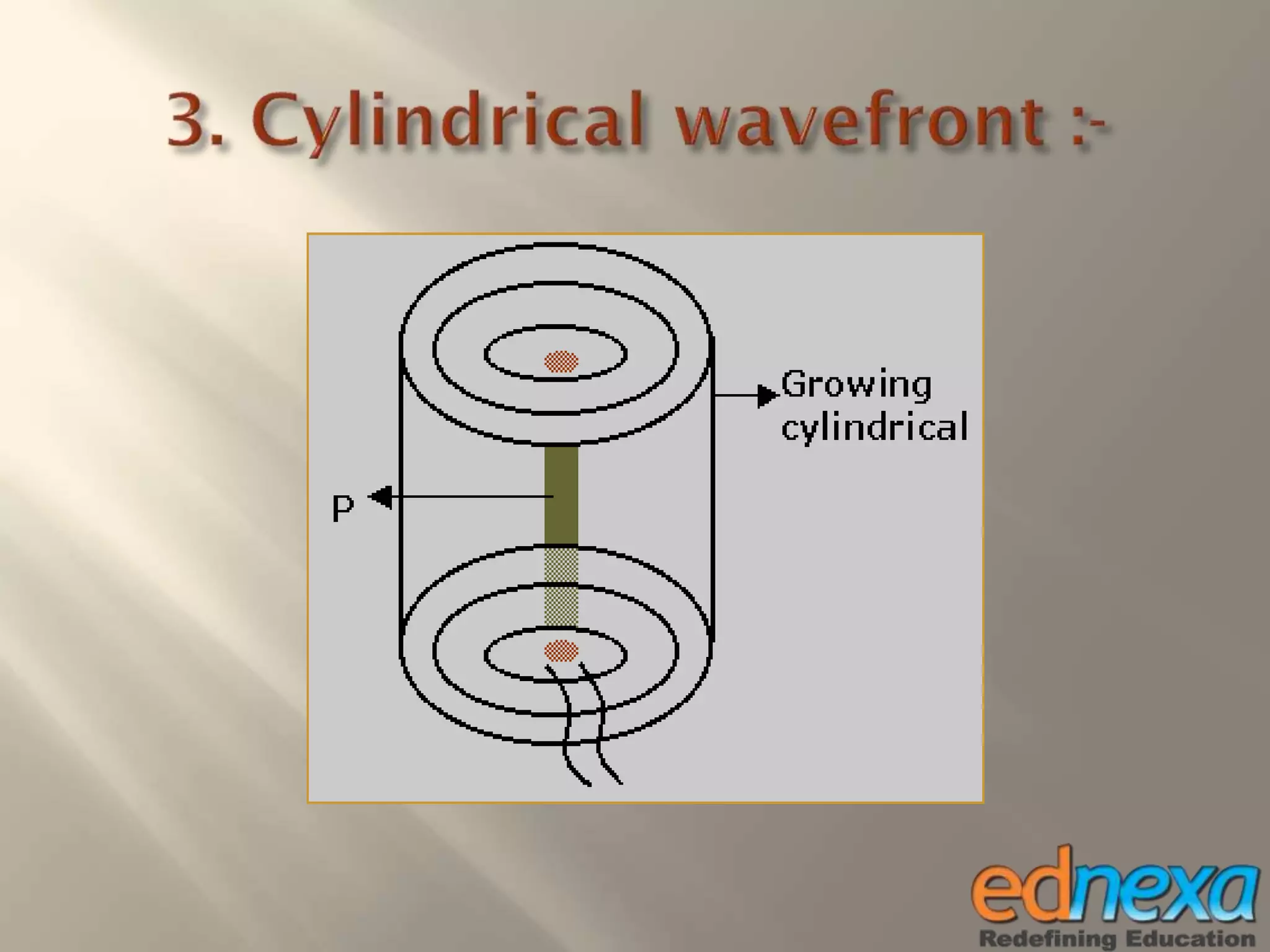
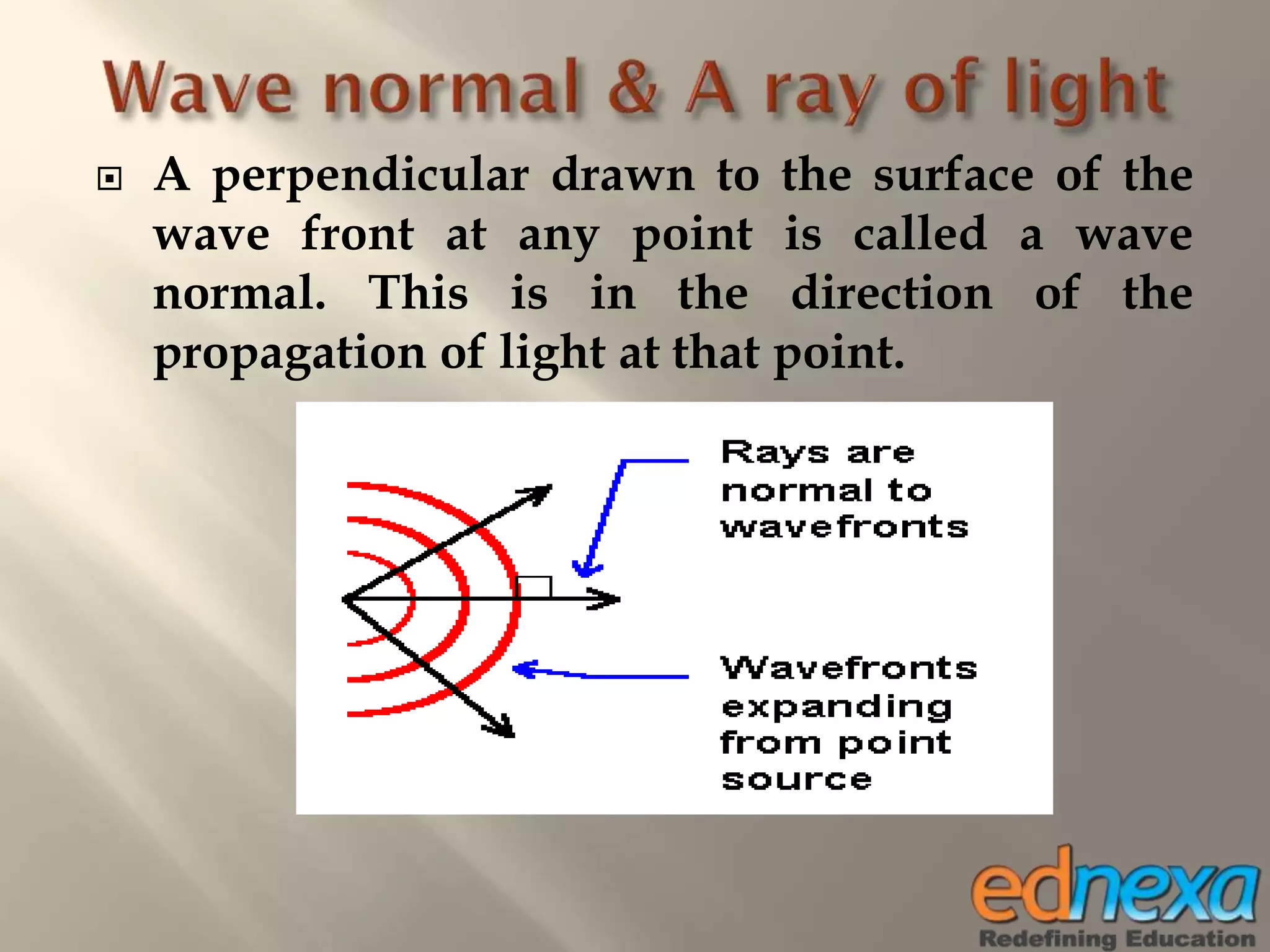
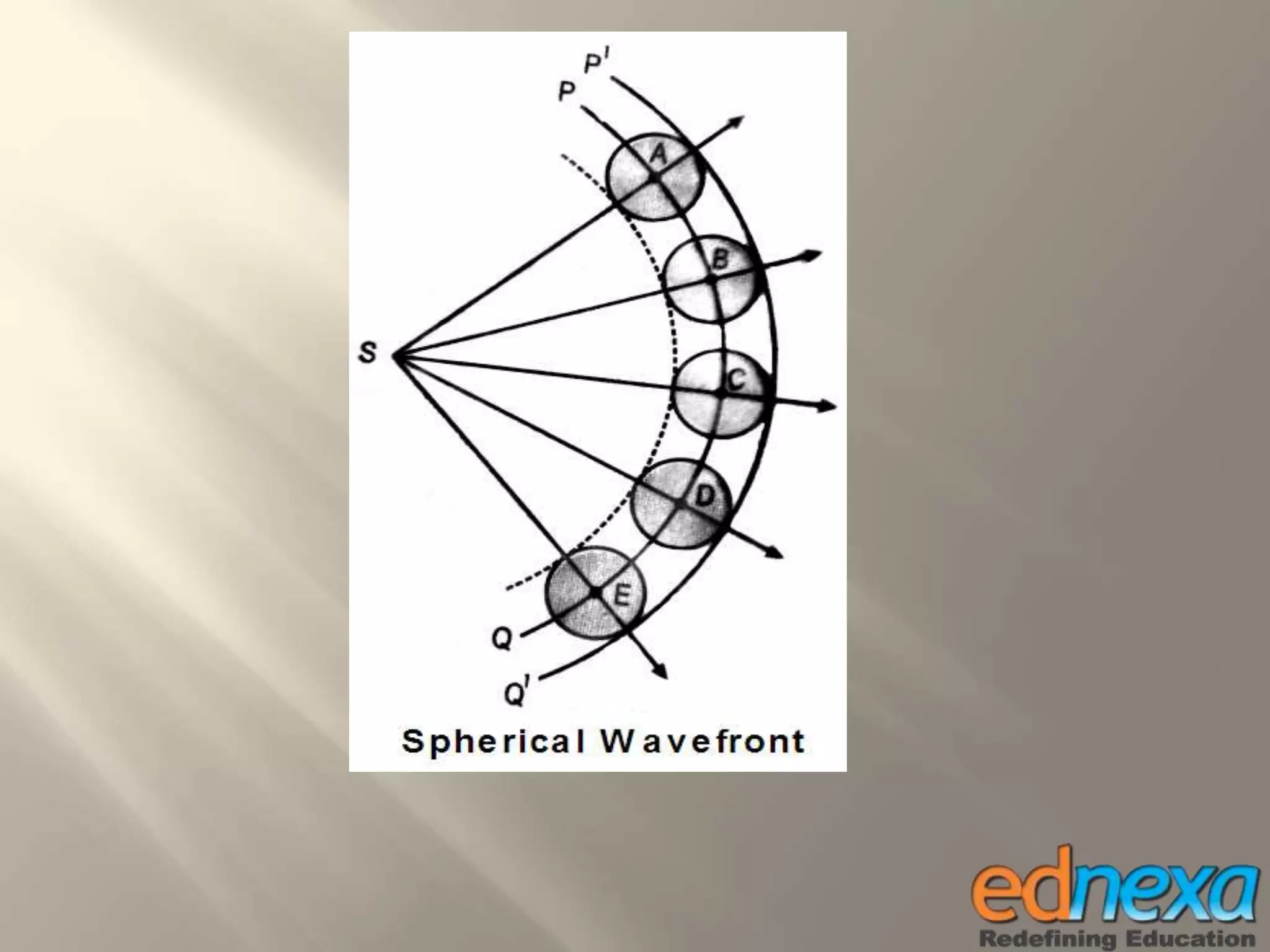
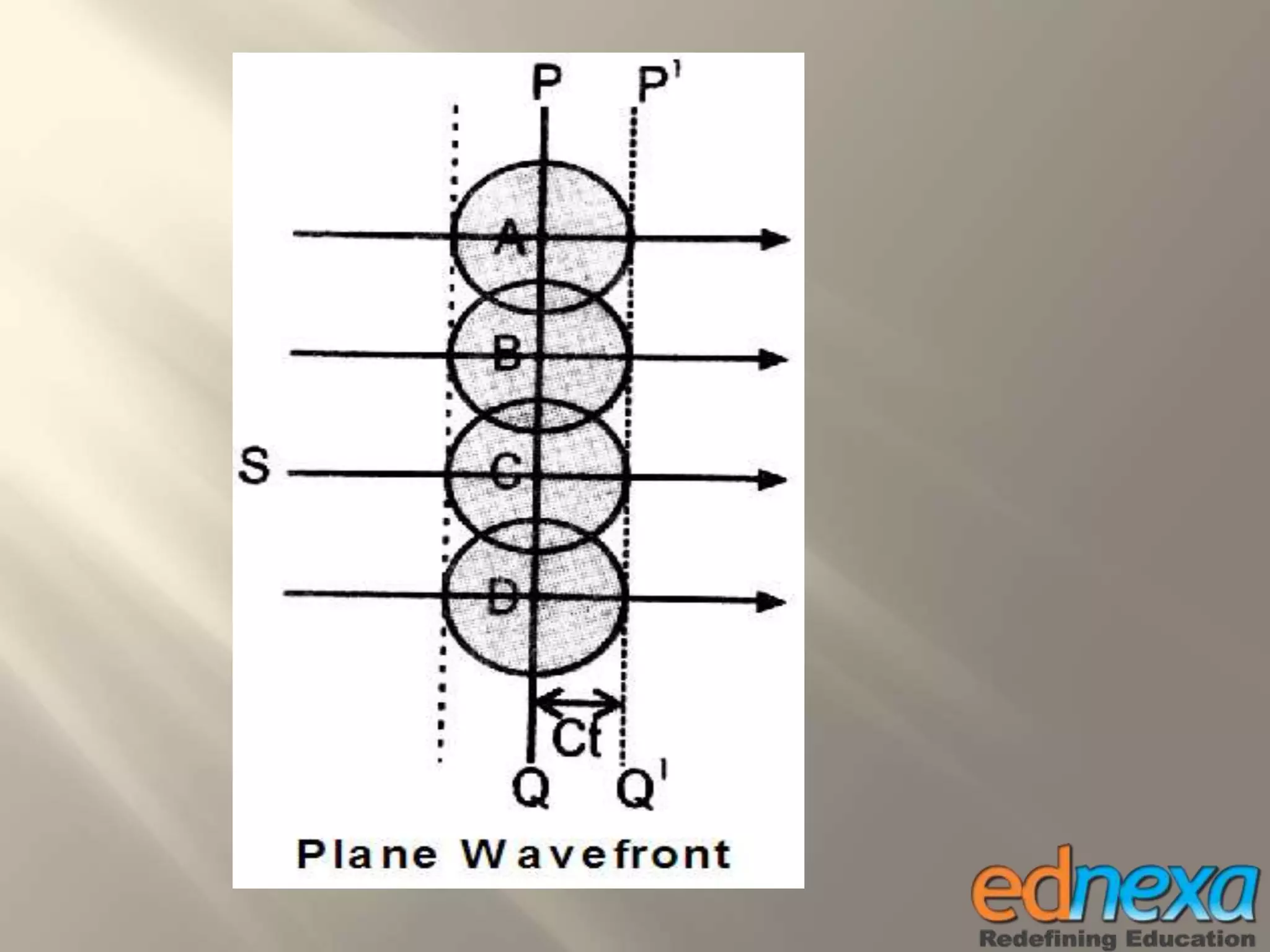
The document outlines Christiaan Huygens' wave theory of light from the 17th century. It proposes that light consists of longitudinal waves that propagate in a straight line through a hypothetical medium called the luminiferous ether. According to the theory, each point on a wavefront acts as a secondary source of waves, and the movement of the wavefront over time can be determined using Huygens' principle and construction. The wave theory was able to successfully explain several optical phenomena like reflection, refraction, and interference of light. However, it could not explain some observations like the rectilinear propagation of light and the photoelectric effect.

1. Proposed By Huygens
Prepared by:- Prof. Dnyanesh Vaidya

3.  Light consists of very Tiny, Elastic, Rigid particles
known as Corpuscular”.
 These corpuscles on emission from the source of
light travel in straight line with high velocity
 When these particles enter the eyes, they
produce image of the object or sensation of
vision.
 Corpuscles of different colours have different
sizes.
 Reflection and refraction of light are because of
repulsive and attractive forces respectively.

4.  Velocity of light in denser medium is greater
than velocity of light in rare medium.
 Newton unable to explain simultaneous
reflection and refraction
 Newton unable to explain polarization and
interference concept.
 Scientist unable to find out relation between
size and colour at larger level. At nano level its
true.

5.  Light is propagated in form of Longitudinal waves.
 These waves are emitted by the source of light and
travel in straight lines with a uniform velocity through
a homogeneous medium.
 When light enter our eyes it creates an optical
impression on the retina. Hence, we get the sensation of
light.
 Different colours are due to different wavelengths of
light waves.
 Light waves are mechanical waves. For propagation of
these waves, a hypothetical medium called
“luminiferous ether” is present everywhere. Light
travels through ether in form of waves.

6.  The phenomena like reflection, refraction,
polarization, simultaneous reflection and
refraction, total internal reflection, diffraction
etc can be successfully explained with this
theory.
 According to Huygens’ theory the speed of
light in denser medium is less than the speed
of light in rarer medium. This conclusion is in
perfect agreement with the experimental
findings.

7.  The existence of so called luminiferous ether,
assumed by Huygens, was not confirmed.
 Rectilinear propagation was not explained by
the theory. It was then justified by Fresnel.
 Diffraction was explained much later.
 This theory could not explain photoelectric
emission.

8.  It can be defined as the locus of all the points
of the medium to which the wave reaches
simultaneously, so that all the points are in
the same phase.

9.  Spherical Wave front :-

12.  A perpendicular drawn to the surface of the
wave front at any point is called a wave
normal. This is in the direction of the
propagation of light at that point.

13.  Every point on a wave front acts as a
secondary source of light, sending out
secondary waves. The envelop of all these
secondary waves, at any later instant, gives
the new wave front at that instant.
 If the nature of the wave front at any instant
is known, we can determine the nature and
the position of the wave front at any later
instant by Huygens’ construction, based on
Huygens’ principle.

14.  1. Consider a known position of a spherical
wave front, at time t = 0 as PQRS
 2. According to Huygens’ principle, as soon as
the wave front is formed, every point on this
wave front will act as a secondary source, and
will start emitting secondary waves.
 3. To determine the position of the wave front
after a time t, we have to draw spheres with
every point on the surface PQRS as centre and
radius equal to ct, where c is the velocity of
light.

15.  4. These spheres will represent secondary
wave fronts. Draw a tangential surface
P’Q’R’S’ to these spheres.
 5. The surface P’Q’R’S’ represents the
position of the wave front after time t. It is
also a spherical wave front.

17.  Consider a known position of a plane wave front, at time
t = 0 as PQRS
 According to Huygens’ principle, as soon as the wave front
is formed, every point on this wave front will act as a
secondary source, and will start emitting secondary waves.
 To determine the position of the wave front after a time t,
we have to draw spheres with every point on the surface
PQRS as centre and radius equal to ct, where c is the
velocity of light.
 These spheres will represent secondary wave fronts. Draw a
tangential surface P’Q’R’S’ to these spheres.
 The surface P’Q’R’S’ represents the position of the wave
front after time t. It is also a plane wave front.

19. Thank You