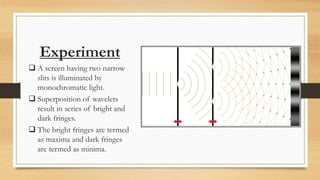
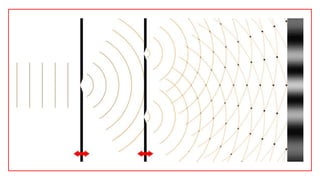
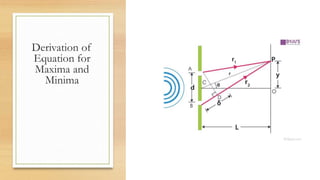
The document summarizes Young's double-slit experiment, which demonstrated the wave-like properties of light. In the experiment, monochromatic light passing through two slits results in a pattern of bright and dark fringes on a screen due to constructive and destructive interference. The document derives the equations that relate the spacing between the fringes to the wavelength of light and the geometry of the double-slit setup. Specifically, it shows that the spacing is directly proportional to the wavelength and distance between slits, and inversely proportional to the separation between the slits.

1. Optics
Presented to: Dr. Kamran sb.
Presented by: Tahir Younus
Reg. No. BS-PHYS-18-44 (E)
Semester: 2018-22 5th
Department of Physics
Ghazi University Dera Ghazi
Khan

2. •Introduction
•Performed by Young in 1801 to demonstrate wave behavior of light.
•In this experiment, Young identified the phenomenon called interference
•The double-slit experiment is a demonstration that light and matter can display
characteristics of both waves and particles.

3. Interference occurred during experiment is of two types
 Constructive Interference
 Destructive Interference

4. Experiment
 A screen having two narrow
slits is illuminated by
monochromatic light.
 Superposition of wavelets
result in series of bright and
dark fringes.
 The bright fringes are termed
as maxima and dark fringes
are termed as minima.

6. Derivation of
Equation for
Maxima and
Minima

7. Maxima
If the point P is to have a bright fringe, the path difference must be an integral multiple of 𝜆.
BD = m𝜆
m = 0,1,2,3,4,….
From ∆𝐴𝐵𝐷.
BD = d sin𝜃
So, d sin𝜃= m𝜆 … . . 1)

8. Distance between Adjacent Bright Fringes
Since angle ‘𝜃’ is very small,
Sin 𝜃 ≈ 𝑇𝑎𝑛𝜃
So, Equation 1 becomes
d𝑇𝑎𝑛𝜃=m 𝜆 … . . 2)
From figure
Tan𝜃=
𝑌
𝐿
So, equation 2 can be written as
d
𝑌
𝐿
= m 𝜆
Y=m
𝜆𝐿
𝑑
… . . 3)

9. If there would be a dark fringe at point P then,
Y=(𝑚 +
1
2
)
𝜆𝐿
𝑑
…. 4)
That’s the distance between two adjacent bright fringes, mth and (m+1) fringes are considered.
For mth bright fringe
𝑦𝑚 = 𝑚
𝜆𝐿
𝑑
For (m+1) bright fringe,
𝑦𝑚+1 = (𝑚 + 1)
𝜆𝐿
𝑑
Let ‘∆𝑌′
be the distance between these two adjacent fringes, then
∆Y=𝑌𝑚+1 − 𝑌𝑚= 𝑚 +
1
2
𝜆𝐿
𝑑
− 𝑚
𝜆𝐿
𝑑
∆Y=
𝜆𝐿
𝑑

10. Minima (Dark fringes)
If the point P is to have a dark fringe, the path difference BD must be half integral number of wavelength
𝜆.
𝐵𝐷 = (𝑚 +
1
2
)𝜆 m=0,1,2,….
From ∆𝐴𝐵𝐷.
BD = d sin𝜃
d sin𝜃 = (𝑚 +
1
2
)𝜆
First dark fringe is obtained at m=0 and second dark for m=1.

11. Distance between adjacent dark fringes
Since angle ‘𝜃’ is very small,
Sin 𝜃 ≈ 𝑇𝑎𝑛𝜃
d𝑇𝑎𝑛𝜃 = (𝑚 +
1
2
)𝜆
From figure,
Tan𝜃=
𝑌
𝐿
d
𝑌
𝐿
= (𝑚 +
1
2
)𝜆
If there would be a dark fringe at ‘p’ then
Y=(𝑚 +
1
2
)
𝜆𝐿
𝑑
Now distance between to adjacent dark fringes,
∆Y=
𝜆𝐿
𝑑

12. Dark and bright fringes are of equal width and are equally spaced.
Fringe spacing is directly proportional to ‘𝜆’ and distance between slits ‘L’.
Inversely to separation of slits ‘d’.