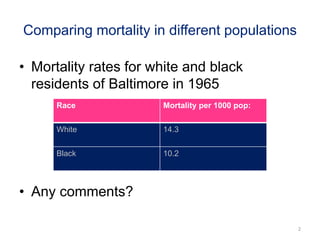
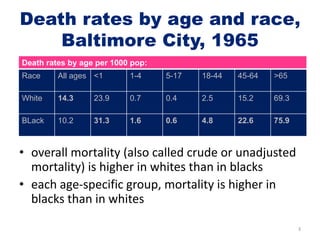
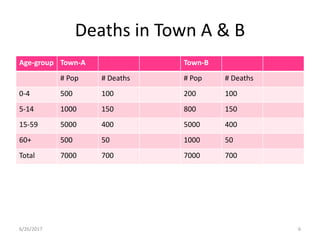
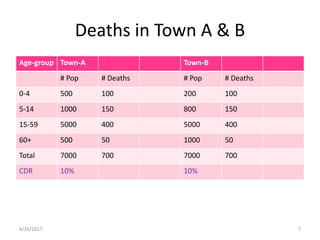
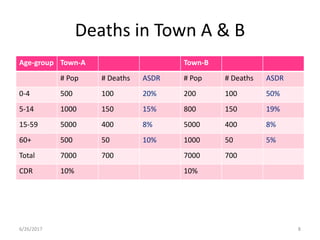
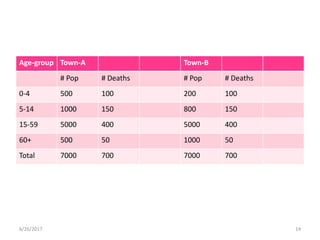
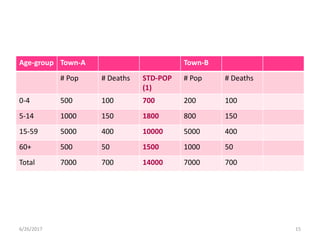
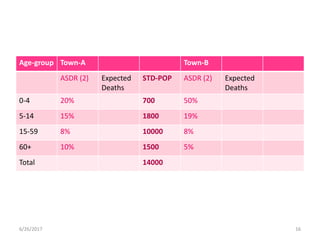
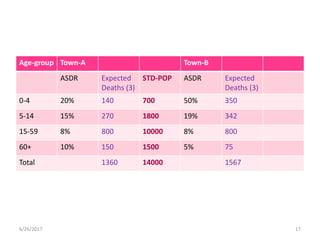
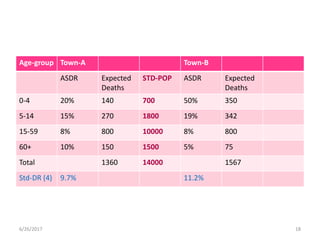
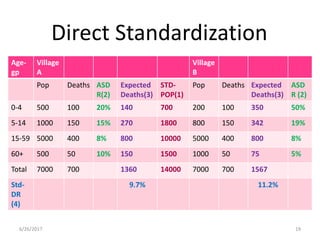
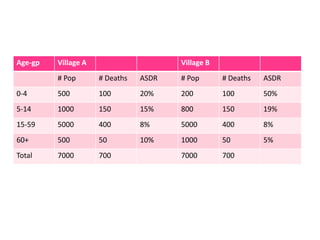
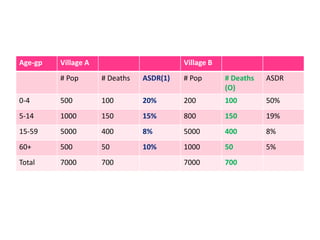
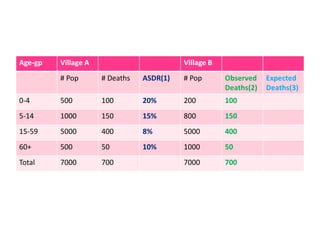
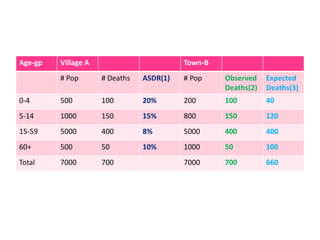
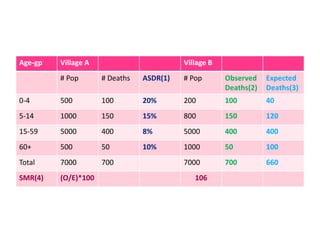
This document discusses methods for standardizing mortality rates to account for differences in population age distributions. Direct standardization uses a standard population to calculate expected mortality rates. Indirect standardization calculates a standardized mortality ratio (SMR) by comparing observed deaths to expected deaths based on a reference population's age-specific death rates. Direct standardization allows comparing absolute mortality rates while indirect standardization expresses differences as a ratio. Standardization is necessary when comparing populations that differ in their age structures.

1. STANDARDIZATION
Dr. Win Aye Hlaing
Lecturer
Department of Epidemiology
University of Public Health, Yangon
6/26/2017 1

2. Comparing mortality in different populations
• Mortality rates for white and black
residents of Baltimore in 1965
• Any comments?
2
Race Mortality per 1000 pop:
White 14.3
Black 10.2

3. Death rates by age and race,
Baltimore City, 1965
• overall mortality (also called crude or unadjusted
mortality) is higher in whites than in blacks
• each age-specific group, mortality is higher in
blacks than in whites
3
Death rates by age per 1000 pop:
Race All ages <1 1-4 5-17 18-44 45-64 >65
White 14.3 23.9 0.7 0.4 2.5 15.2 69.3
BLack 10.2 31.3 1.6 0.6 4.8 22.6 75.9

4. Different Rates
• Crude
• Specific
• Standardized
6/26/2017 4

5. Crude Death Rate
&
Age Specific Death Rate
6/26/2017 5

6. Deaths in Town A & B
Age-group Town-A Town-B
# Pop # Deaths # Pop # Deaths
0-4 500 100 200 100
5-14 1000 150 800 150
15-59 5000 400 5000 400
60+ 500 50 1000 50
Total 7000 700 7000 700
6/26/2017 6

7. Deaths in Town A & B
Age-group Town-A Town-B
# Pop # Deaths # Pop # Deaths
0-4 500 100 200 100
5-14 1000 150 800 150
15-59 5000 400 5000 400
60+ 500 50 1000 50
Total 7000 700 7000 700
CDR 10% 10%
6/26/2017 7

8. Deaths in Town A & B
Age-group Town-A Town-B
# Pop # Deaths ASDR # Pop # Deaths ASDR
0-4 500 100 20% 200 100 50%
5-14 1000 150 15% 800 150 19%
15-59 5000 400 8% 5000 400 8%
60+ 500 50 10% 1000 50 5%
Total 7000 700 7000 700
CDR 10% 10%
6/26/2017 8

9. • Approaches for dealing this problem
– Direct Age adjustment
– Indirect Age adjustment (Standardized
Mortality Ratios)
9

10. Standardized Rate
6/26/2017 10

11. I. Direct Standardization

12. • A standard population is used to eliminate effects of
difference in age between populations
• A hypothetical “standard” population is created
• The simple way is to combine these populations
• Then, apply both the age-specific mortality rates
(ASDR) of each population to standard population
12

13. • derive the expected number of deaths in both
early and late period
• It means that we want to see what deaths
would be if they were equal to standard
population
• Dividing each of these two total expected
numbers of deaths by the total standard
population, we can calculate an expected
mortality rate in the standard population
• These are called age-adjusted rates

14. Age-group Town-A Town-B
# Pop # Deaths # Pop # Deaths
0-4 500 100 200 100
5-14 1000 150 800 150
15-59 5000 400 5000 400
60+ 500 50 1000 50
Total 7000 700 7000 700
6/26/2017 14

15. Age-group Town-A Town-B
# Pop # Deaths STD-POP
(1)
# Pop # Deaths
0-4 500 100 700 200 100
5-14 1000 150 1800 800 150
15-59 5000 400 10000 5000 400
60+ 500 50 1500 1000 50
Total 7000 700 14000 7000 700
6/26/2017 15

16. Age-group Town-A Town-B
ASDR (2) Expected
Deaths
STD-POP ASDR (2) Expected
Deaths
0-4 20% 700 50%
5-14 15% 1800 19%
15-59 8% 10000 8%
60+ 10% 1500 5%
Total 14000
6/26/2017 16

17. Age-group Town-A Town-B
ASDR Expected
Deaths (3)
STD-POP ASDR Expected
Deaths (3)
0-4 20% 140 700 50% 350
5-14 15% 270 1800 19% 342
15-59 8% 800 10000 8% 800
60+ 10% 150 1500 5% 75
Total 1360 14000 1567
6/26/2017 17

18. Age-group Town-A Town-B
ASDR Expected
Deaths
STD-POP ASDR Expected
Deaths
0-4 20% 140 700 50% 350
5-14 15% 270 1800 19% 342
15-59 8% 800 10000 8% 800
60+ 10% 150 1500 5% 75
Total 1360 14000 1567
Std-DR (4) 9.7% 11.2%
6/26/2017 18

19. 6/26/2017 19
Age-
gp
Village
A
Village
B
Pop Deaths ASD
R(2)
Expected
Deaths(3)
STD-
POP(1)
Pop Deaths Expected
Deaths(3)
ASD
R (2)
0-4 500 100 20% 140 700 200 100 350 50%
5-14 1000 150 15% 270 1800 800 150 342 19%
15-59 5000 400 8% 800 10000 5000 400 800 8%
60+ 500 50 10% 150 1500 1000 50 75 5%
Total 7000 700 1360 14000 7000 700 1567
Std-
DR
(4)
9.7% 11.2%
Direct Standardization

20. Indirect Standardization
(Standardized Mortality Ratios-SMR)

21. Indirect Standardization
• Select (or) Create standard rate
• The simple way is to choose one of them
• Then apply ASDR of selected population
(i.e., standard death rate) to the other
population
• It means that we want to see what deaths
would be if the other population had the
same rate (ASDR)
• Then estimate SMR & compare to 100
6/26/2017 21

22. Observed no. of deaths per year
• SMR= x100
Expected no. of deaths per year
• SMR is calculated by totaling the Observed number of
deaths and dividing it by the expected number of
deaths
22

23. • SMR =100 (observed same as expected)
• SMR <100 (Observed less than expected)
• SMR ˃100 (Observed more than expected)
• Multiplication by 100 is done to yield results
without decimals
6/26/2017 23

24. Used when..
• No. of deaths from each age specific
stratum are not available
• Studying mortality in an occupationally
exposed population
6/26/2017 24

25. Example of Indirect Age Adjustment

26. Age-gp Village A Village B
# Pop # Deaths ASDR # Pop # Deaths ASDR
0-4 500 100 20% 200 100 50%
5-14 1000 150 15% 800 150 19%
15-59 5000 400 8% 5000 400 8%
60+ 500 50 10% 1000 50 5%
Total 7000 700 7000 700

27. Age-gp Village A Village B
# Pop # Deaths ASDR(1) # Pop # Deaths
(O)
ASDR
0-4 500 100 20% 200 100 50%
5-14 1000 150 15% 800 150 19%
15-59 5000 400 8% 5000 400 8%
60+ 500 50 10% 1000 50 5%
Total 7000 700 7000 700

28. Age-gp Village A Village B
# Pop # Deaths ASDR(1) # Pop Observed
Deaths(2)
Expected
Deaths(3)
0-4 500 100 20% 200 100
5-14 1000 150 15% 800 150
15-59 5000 400 8% 5000 400
60+ 500 50 10% 1000 50
Total 7000 700 7000 700

29. Age-gp Village A Town-B
# Pop # Deaths ASDR(1) # Pop Observed
Deaths(2)
Expected
Deaths(3)
0-4 500 100 20% 200 100 40
5-14 1000 150 15% 800 150 120
15-59 5000 400 8% 5000 400 400
60+ 500 50 10% 1000 50 100
Total 7000 700 7000 700 660

30. Age-gp Village A Village B
# Pop # Deaths ASDR(1) # Pop Observed
Deaths(2)
Expected
Deaths(3)
0-4 500 100 20% 200 100 40
5-14 1000 150 15% 800 150 120
15-59 5000 400 8% 5000 400 400
60+ 500 50 10% 1000 50 100
Total 7000 700 7000 700 660
SMR(4) (O/E)*100 106

31. Summary
• Not a real
• Just to control the effect of unequal
distribution in comparison
• It means that “to control confounding factor”
6/26/2017 31

32. THANK YOU!!
6/26/2017 32