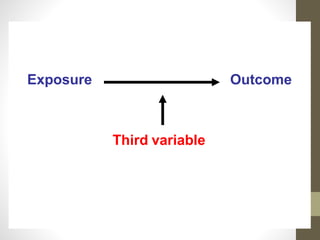
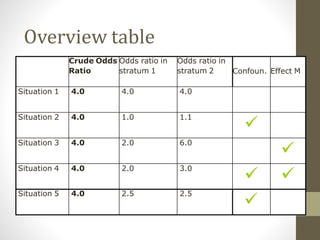
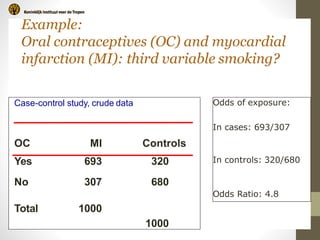
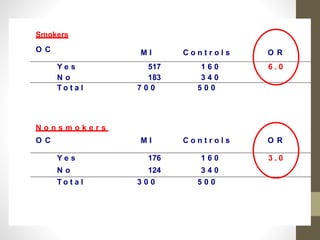
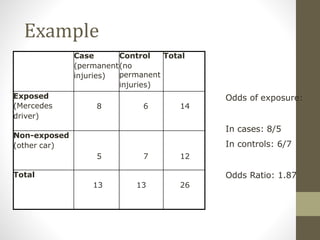
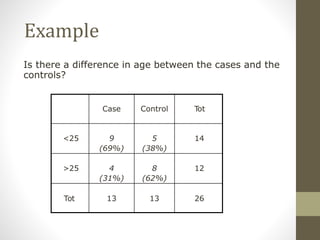
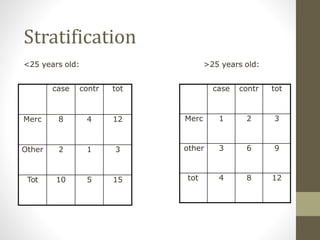
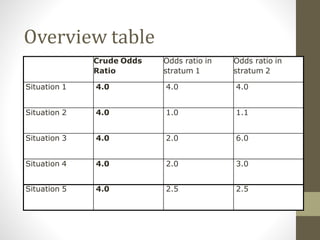
1. Effect modification and confounding are two aspects to consider when examining the relationship between an exposure and outcome. Effect modification provides useful information about how a third variable impacts the relationship, while confounding can distort the observed effect. 2. Stratifying the data and calculating stratum-specific odds ratios is a way to check for effect modification and confounding. Effect modification is present if the odds ratios differ substantially between strata. Confounding is present if the crude odds ratio differs from the stratified odds ratios. 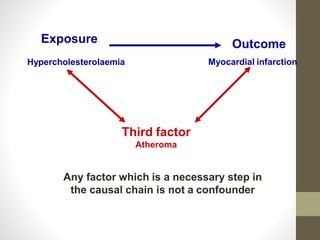3. It is important to measure potential confounding factors so they can be controlled for through stratification or multivariate analysis. This prevents confounding from distorting the observed effect between the exposure and outcome.

1. CONFOUNDER AND EFFECT
MODIFICATION

2. Exposure Outcome
Third variable

3. Two aspects to consider
(1) Effect modifier
(2) Confounding factors
- Useful information
- Distortion of the effect

4. •Variation in the magnitude of measure of effect depending on a
third variable
•Effect modification is not a bias but useful information
Effect modification/Interaction
Happens when RR or OR
is different between subgroups of
population

5. Example:
Oral contraceptives (OC) and myocardial
infarction (MI): third variable smoking?
Case-control study, crude data Odds of exposure:
In cases: 693/307
OC MI Controls
Yes 693 320 In controls: 320/680
No 307 680
Odds Ratio: 4.8
Total 1000
1000

6. Smokers
O C M I C o n t r o l s O R
Y e s 517 1 6 0 6 . 0
N o 183 3 4 0
T o t a l 7 0 0 5 0 0
N o n s m o k e r s
O C M I C o n t r o l s O R
Y e s 176 1 6 0 3 . 0
N o 124 3 4 0
T o t a l 3 0 0 5 0 0

7. Interpretation
What do those 2 different OR mean?
-Taking Oral Contraceptives is a risk factor for Myocardial
Infarction, especially in people that smoke.
Among smokers, the odds of finding someone who takes OC
among the cases is 6 times the odds of finding someone taking
OC among the controls.
Among non smokers finding someone who takes OC among the
cases is “only” 3 times the odds of finding someone taking OC
among the controls.

8. Terminology
Crude OR= 4.8 are presented after univariate analysis: only
looking at one variable, not taking other factors into account
Dividing the exposed and unexposed or cases and controls into
subgroups for analysis is called ‘stratification’.
Stratum specific OR for smokers= 6.0
Stratum specific OR for non-smokers= 3.0
If two subgroups have (very) different OR or RR, there is ‘effect
modification’ or ‘interaction’

9. Effect modifier
If effect modification is present: always show stratum specific
OR or RR in order to be able to direct control measures
An effect modifier provides insight in how the disease works and
is related to the ‘causal pathway’ of a disease
More examples:
Hypertension is more likely to cause myocardial infarction in
people with hypercholesterolaemia then in people without
hypercholesterolaemia
•Malaria causes more deaths in pregnant women
•Measles causes more deaths in malnourished children than in
healthy children

10. Confounding
(Partially-) alternative explanation for an association
found between an exposure and an outcome.

11. Example
Case
(permanent
injuries)
Control
(no
permanent
injuries)
Total
Exposed
(Mercedes
driver)
8 6 14
Non-exposed
(other car)
5 7 12
Total
13 13 26
Odds of exposure:
In cases: 8/5
In controls: 6/7
Odds Ratio: 1.87

12. Example
Odds Ratio: 1.87
The odds of finding someone who drives a Mercedes among the
cases (with permanent injuries) is about 1.9 times (almost
twice) the odds of finding someone that drives a Mercedes
among the controls.
Assuming this OR is significant:
Would you advice Mercedes to urgently increase the safety from
their cars?

13. Example
Is there a difference in age between the cases and the
controls?
Case Control Tot
<25 9
(69%)
5
(38%)
14
>25 4
(31%)
8
(62%)
12
Tot 13 13 26

14. Example
So perhaps age could be a confounder of the relationship
between the exposure (Mercedes) and outcome (permanent
injuries)
But how do we check if age was indeed a
confounder?

15. Stratification
If you suspect confounding, you could control for it by
analysing in 2 or more strata.
This is called stratification.
In the example this means that you would calculate odds and
odds ratios separately for each value (or value group) in the
variable “age”.
So we do separate analysis:
in the people <25 years of age
in the people >25 years of age

16. Stratification
<25 years old: >25 years old:
case contr tot
Merc 8 4 12
Other 2 1 3
Tot 10 5 15
case contr tot
Merc 1 2 3
other 3 6 9
tot 4 8 12

17. Stratification
<25 years >25 years
Odds in cases: 8/2 Odds in cases: 1/3
Odds in controls: 4/1 Odds in controls: 2/6
Odds Ratio = 1.0 Odds Ratio 1.0
These OR are called STRATUM SPECIFIC ODDS RATIOS
The OR in the whole population is called the CRUDE ODDS RATIO
What do the stratum specific OR mean?

18. Stratification
Interpretation
The risk of permanent injuries in drivers <25 years is higher
than in drivers >25 years, but it does not depend on the car
type they are driving in (stratum specific odds ratios were 1).
Age was a confounder for the found relationship between
driving a Mercedes and permanent injuries.
The ones driving the Mercedes were (on average) younger than
the people driving another car. That made it appear as if car
type and outcome were associated, where in fact it was age and
outcome.

19. Confounding
• Third variable
• Be associated with exposure
• - without being the consequence of exposure
• Be associated with outcome
• - independently of exposure
• And to act as a confouder, the factor must be distributed unevenly between
cases and controls (case control study) or exposed and non exposed (cohort
study)
To be a potential confounding factor, 2 conditions must be met:
Exposure Outcome

20. Examples of commonpotential confounders
Age
Sex
Socio economic status
Living conditions
Etc..
Depending on the relationship you are interested in you can
guess which factors might be potential confounders but you
cannot be sure beforehand..

21. Exposure
Hypercholesterolaemia
Outcome
Myocardial infarction
Third factor
Atheroma
Any factor which is a necessary step in
the causal chain is not a confounder

22. Confounding
(OR or RR)Distortion of measure of effect
because of a third factor
Should be prevented or
Needs to be controlled for

23. How to prevent/control confounding?
Prevention
• Restriction to one stratum (cohort with only women, only
cases and controls between 30-50 years old)
• Matching (if you have a male case, find a male control)
Control
• Stratified analysis
• Multivariate analysis (several confounding factors at the
same time)

24. Control for confounding
• But it is very important that you measure potential
• confounders!! If we had not asked the drivers about
• their age we could not have corrected for age group!
In contrast to bias: Even after data collection you can
correct/adjust for confounding.

25. Effect modifier
Belongs to nature
Different effects in different strata
Simple
Useful
Increases knowledge of biological mechanism
Allows targeting of PH action
Confounding factor
Belongs to study
Stratefied OR different from crude OR
Distortion of effect
Creates confusion in data
Prevent (in protocol phase <e.g. matching
randomization>)
Control (in analysis phase <if you have measured
it!!>)
To summarize:

26. To summarize: stratified
analysis
• Perform crude analysis
• Measure the strength of association
• List potential effect modifiers and confounders
• Stratify data according to potential modifiers or
confounders
• Check for effect modification
• If effect modification present, show the data by stratum
• If no effect modification present, check for confounding
• If confounding, show adjusted data
• If no confounding, show crude data

27. How to check:
Effect modifier: different effect in different strata
Confounding: different effect between the crude
and the ‘adjusted’ OR or RR

28. Overview table
Crude Odds
Ratio
Odds ratio in
stratum 1
Odds ratio in
stratum 2
Situation 1 4.0 4.0 4.0
Situation 2 4.0 1.0 1.1
Situation 3 4.0 2.0 6.0
Situation 4 4.0 2.0 3.0
Situation 5 4.0 2.5 2.5

29. Overview table
Crude Odds
Ratio
Odds ratio in
stratum 1
Odds ratio in
stratum 2 Confoun. Effect M
Situation 1 4.0 4.0 4.0
Situation 2 4.0 1.0 1.1

Situation 3 4.0 2.0 6.0

Situation 4 4.0 2.0 3.0
 
Situation 5 4.0 2.5 2.5
