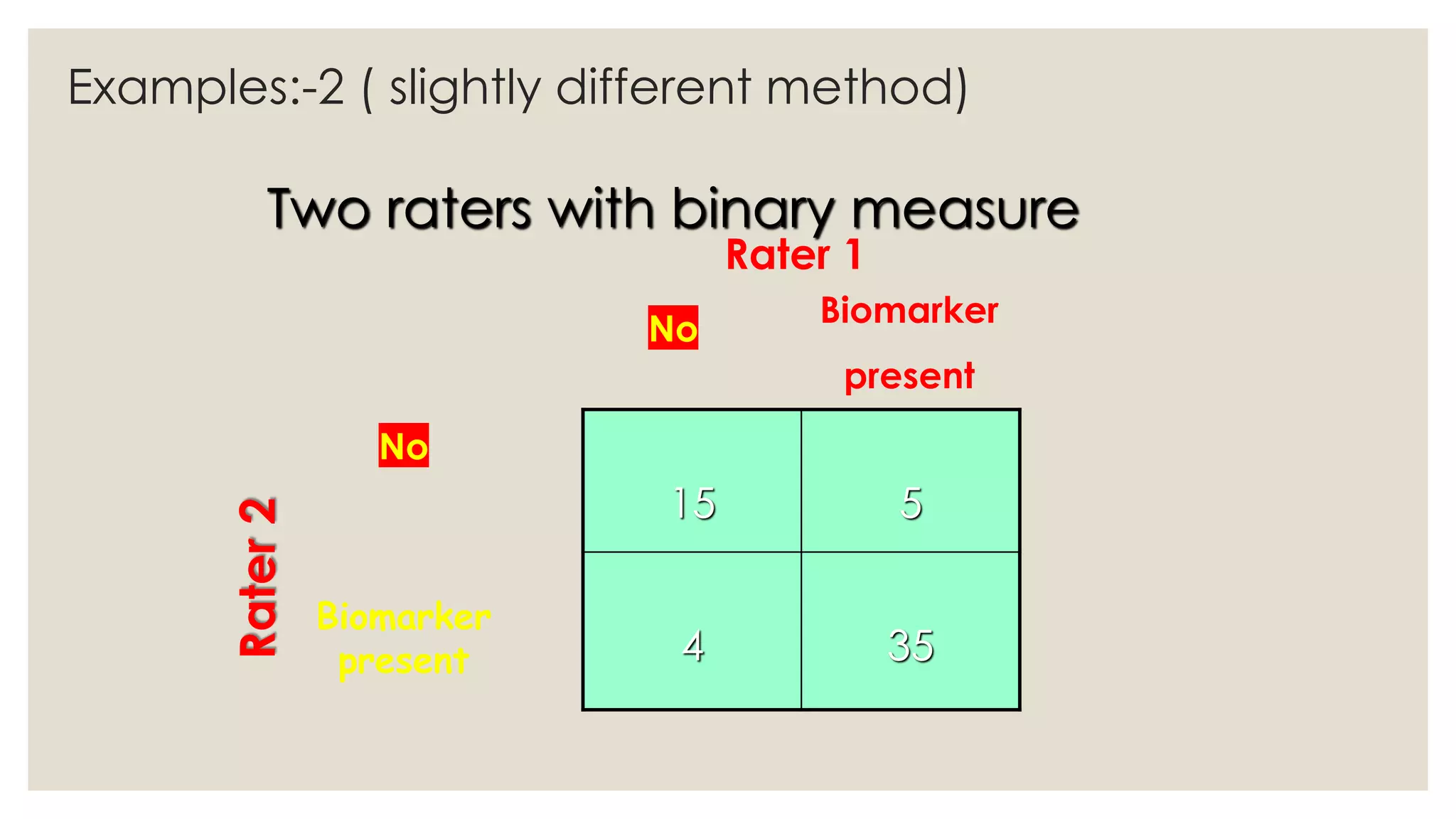
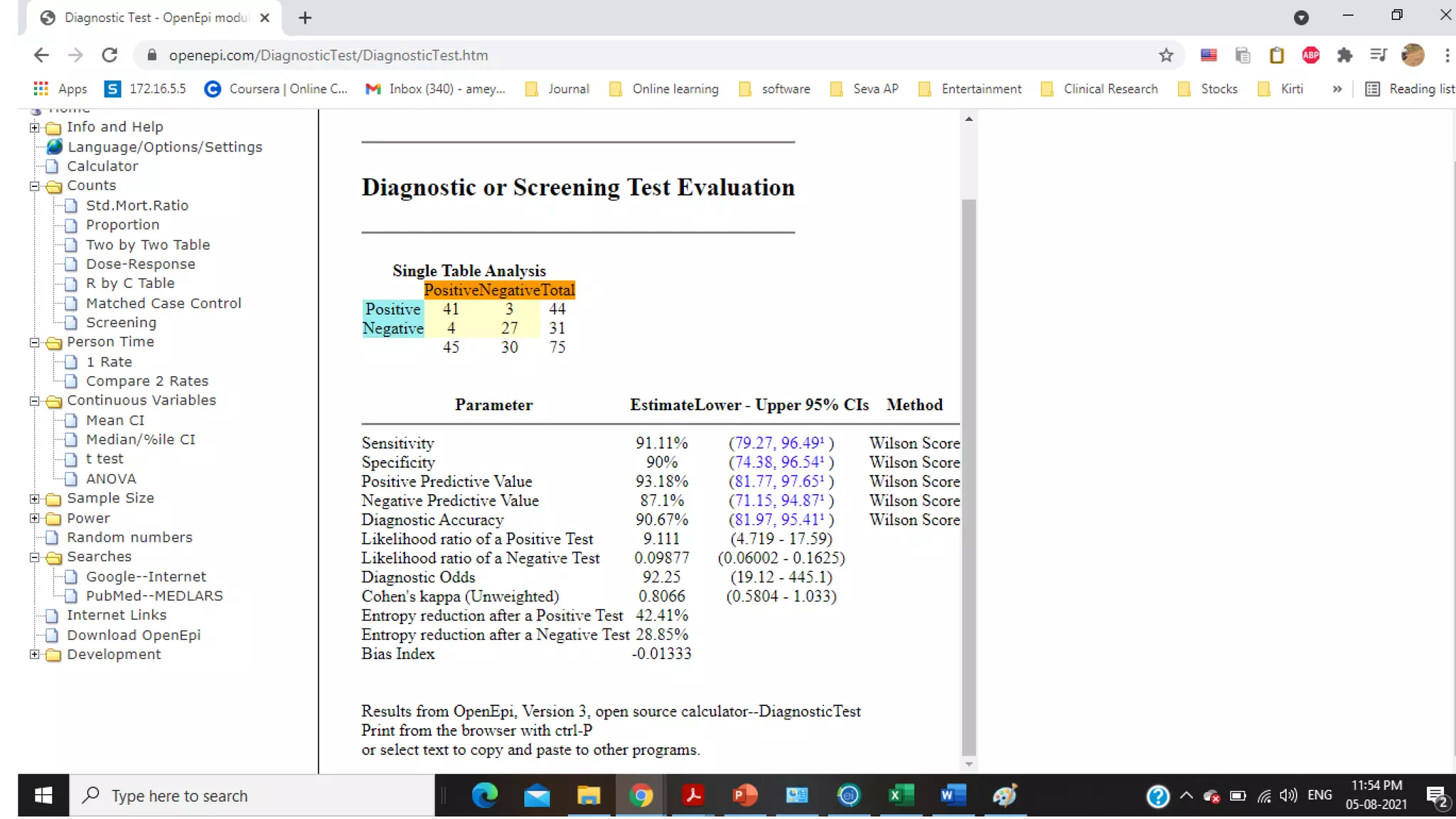
This document discusses kappa statistics, which measure interrater reliability beyond chance agreement. Kappa statistics are useful when multiple raters are interpreting subjective data, such as radiology images. The kappa statistic formula calculates observed agreement between raters compared to expected chance agreement. Examples show how to calculate kappa when two raters are assessing whether a biomarker is present or absent in samples. Confidence intervals for kappa are determined using 1.96 as a constant to generate a 95% confidence level.

1. DATA-BASE MANAGEMENT
Kappa statistics
DR. AMEY DHATRAK

2. Kappa statistics
◦ The kappa statistic is frequently used to test interrater reliability.(Measurement of the extent to
which data collectors (raters) assign the same score to the same.)
◦ Why we need Kappa???
◦ Some studies involve the need for some degree of subjective interpretation by observers and
often measurement differs with different ‘raters.
◦ intraobserver variation
◦ intrasubject variation
◦ For example:
◦ Interpreting x-ray results = Two radiologists reading same chest x-ray for signs of pneumoconiosis
◦ Two laboratory scientists counting radioactively marked cells from liver tissue
◦ Often same rater differs when measuring the same thing on a different occasion

3. Kappa- agreement
◦ Without good agreement results are difficult to interpret
◦ Measurements are unreliable or inconsistent
◦ Need measures of agreement - kappa
◦ Remember-
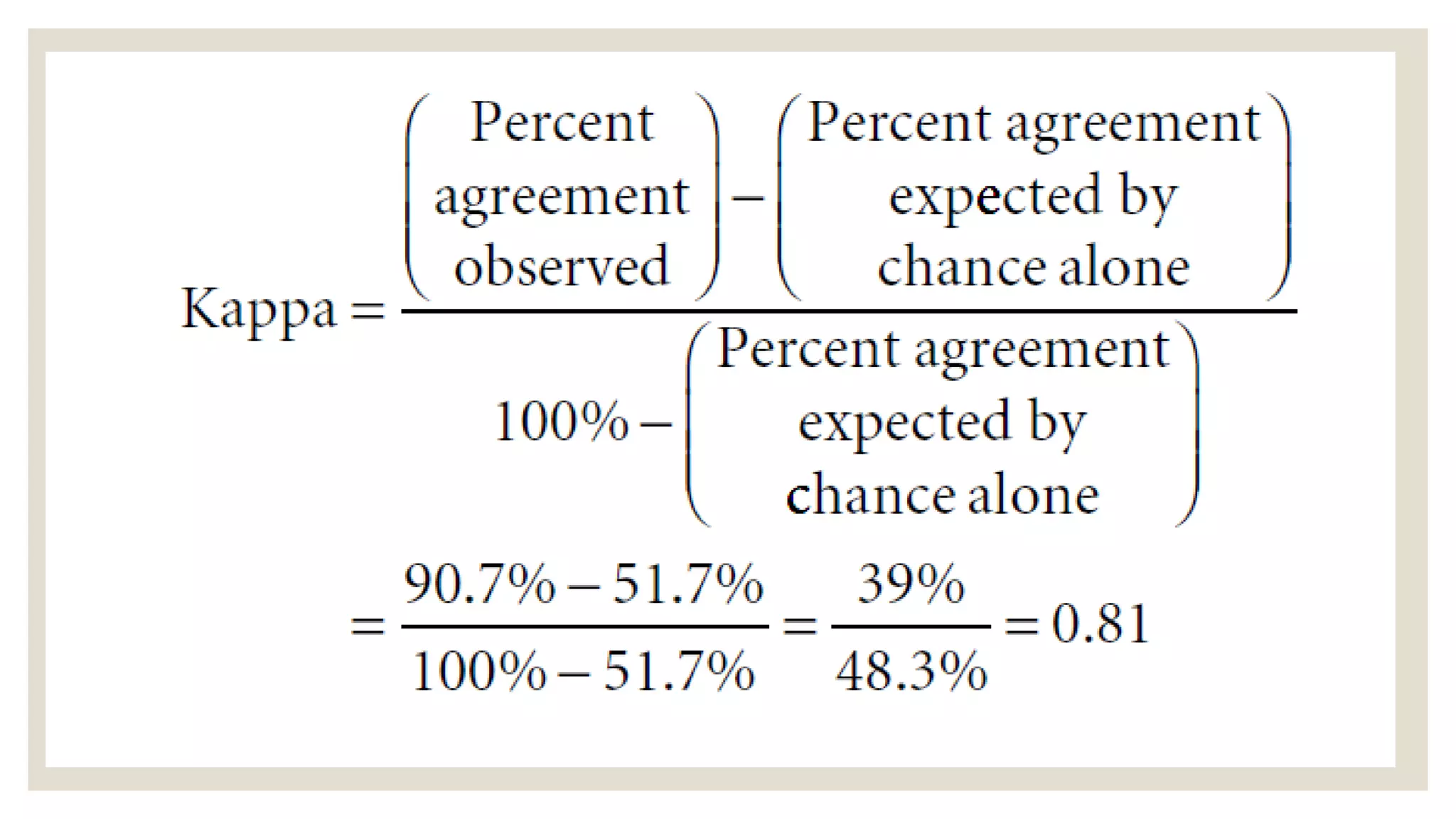
Extent to which the observed agreement exceeds that which would be expected by
chance alone (i.e., percent agreement observed − percent agreement expected by
chance alone) [numerator] relative to the maximum that the observers could hope to
improve their agreement (i.e., 100% − percent agreement expected by chance alone)
[denominator].

4. Formula



+
+
+
+
−
−
=
i
i
i
i
ii






1

5. Examples:-1
44*60/100= 26.4
31*40/100= 12.4

8. Two raters with binary measure
15 5
4 35
No
Biomarker
present
No
Biomarker
present
Rater 1
Rater
2
Examples:-2 ( slightly different method)

9. Cohen’s Kappa Statistic (κ)
Measures agreement between raters more than expected by chance



+
+
+
+
−
−
=
i
i
i
i
ii






1
 represents the marginal probabilities and i = 1,2 the score

10. Two raters with binary measure
15 5 20
4 35 39
19 40 59
No Biomarker
present
No
Biomarker
present
Rater 1
Rater
2
Marginal Total
Marginal
Total

11. Two raters with binary measure
15 5 20
4 35 39
19 40 59
ii = (15 + 35)/59
= 0.847
i++i = (20x19 + 40x39)/592
= 0.557

12. Two raters with binary measure
15 5 20
4 35 39
19 40 59
ii = 0.847
i++i = 0.557



+
+
+
+
−
−
=
i
i
i
i
ii






1
557
.
0
1
557
.
0
847
.
0
−
−
=
 654
.
0
=


14. Confidence intervals for kappa
◦ Given that the most frequent value desired is 95%, the formula uses
1.96 as the constant.
◦ The formula for a confidence interval = κ – 1.96 x SEκ to κ + 1.96 x Seκ
◦ To obtain the standard error of kappa (SEκ) the following formula
should be used:

17. Thank You