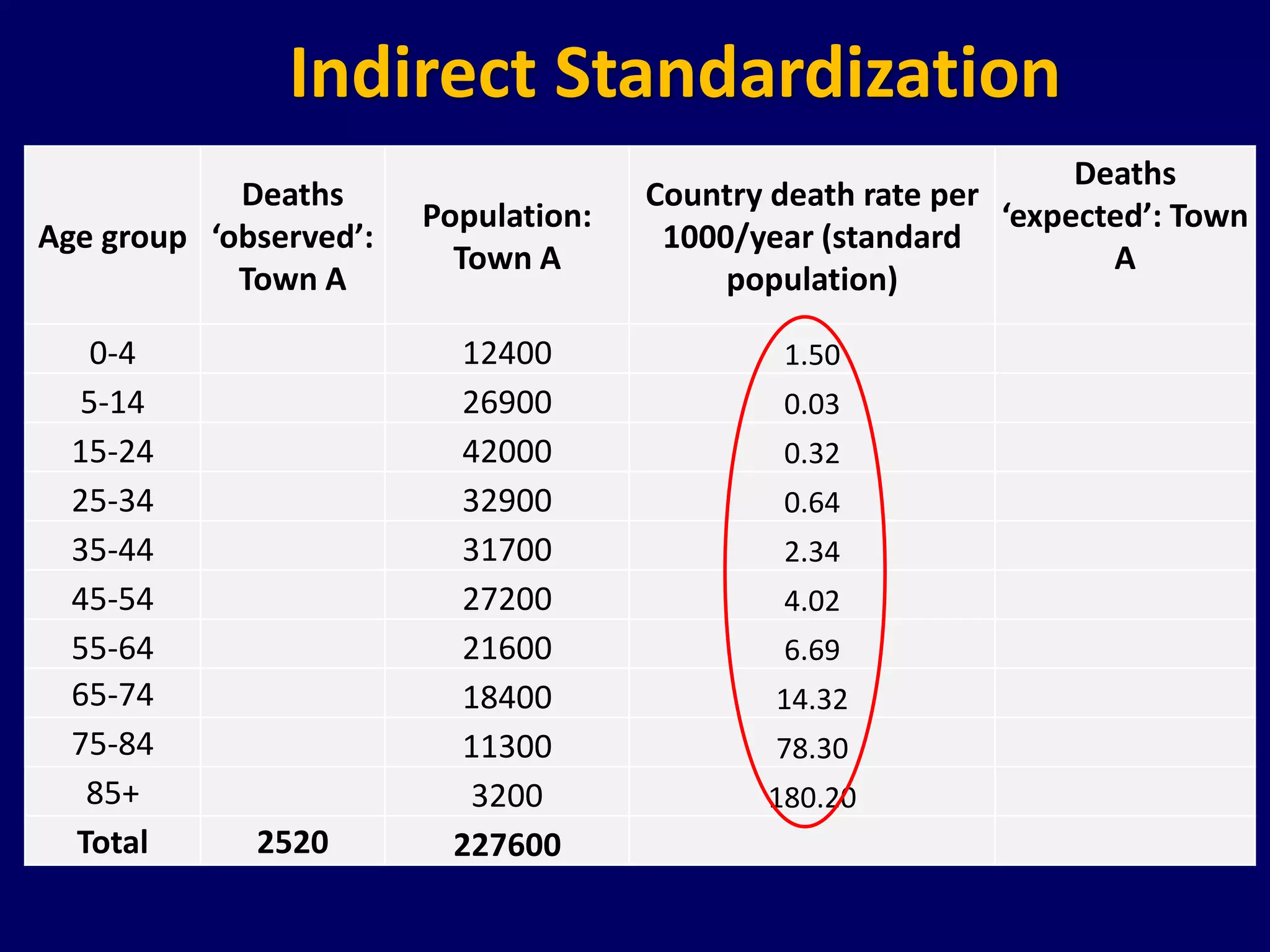
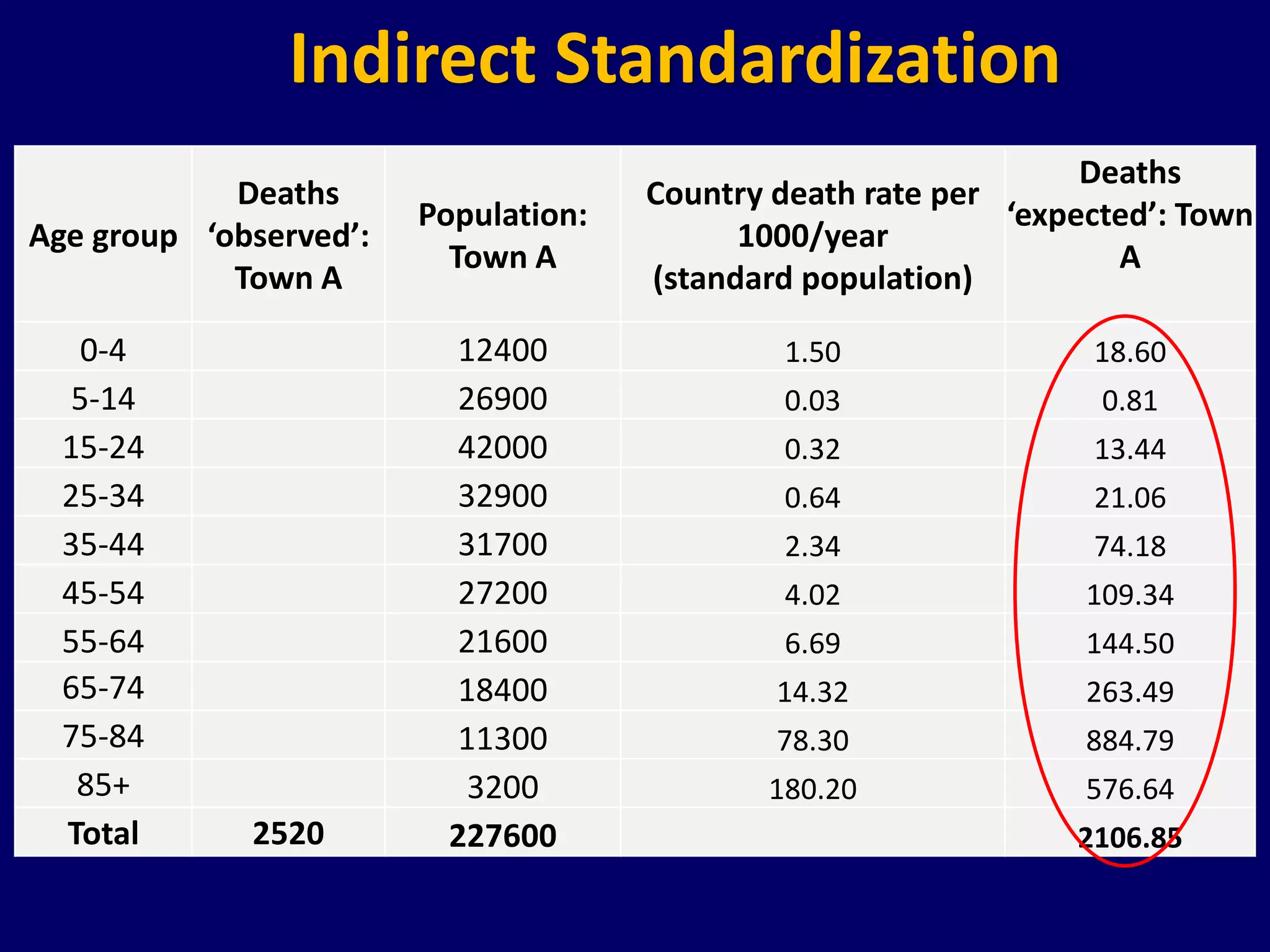
The document discusses the standardization of mortality rates between two towns with differing socioeconomic characteristics and age distributions. It explains indirect and direct methods of standardization to derive standardized mortality ratios (SMR) and age-adjusted death rates, concluding that town A has higher mortality compared to the country average, while town B's mortality is similar to the standard population. The document emphasizes the importance of standardization in comparing mortality rates effectively by adjusting for age and other factors.

1. STANDARDIZATION OF RATES
Halyna Lugova, MD, PhD October 8, 2014

2. Standardization of Rates:
Town B: affluent rural community, popular retirement area
The all-cause crude death rate – 14.2 per 1,000/year in 2013
2
Town A: high unemployment rates, poverty
The all-cause crude death rate – 11.1 per 1,000/year in 2013
This suggests that mortality is higher in Town B although this is not what we would expect given socioeconomic characteristics of the two towns

3. Standardization of Rates: Age distribution for two populations
3
0
5
10
15
20
25
30
35
40
45
0-4
5-14
15-24
25-34
35-44
45-54
55-64
65-74
75-84
85 and
over
Town A
Town B
X 1,000 population
age

4. Standardization of Rates
4
Town A has a younger population, therefore it has a lower death rate.
How to compare the two towns, independently of the effects of this difference in age distribution?
We need to have a summary measure of mortality for all age groups to avoid many tables of rates for each age group.
Such summary measure that takes account of the differences in age distribution of the two areas could be derived by a technique called standardization.

5. Standardization of Rates
1.The indirect method provides standardized mortality ratio (SMR) and indirectly standardized rates
2.The direct method provides directly standardized rates
3.For indirect method we need to select standard population, e.g. country population, or one of the ‘standard populations’ (not real) created to represent population structure: World standard population, European standard population, etc.
5

6. Indirect Standardization
–First, we will calculate the SMR for Town A
1.We need to know total number of deaths (‘observed’) in Town A in 2013
2.We need to know the population in Town A in each age group in 2013

7. Indirect Standardization
Age group
Deaths ‘observed’: Town A
Population:
Town A
Country death rate per 1000/year
(standard population)
Deaths ‘expected’: Town A
0-4
12400
5-14
26900
15-24
42000
25-34
32900
35-44
31700
45-54
27200
55-64
21600
65-74
18400
75-84
11300
85+
3200
Total
2520
227600

8. Indirect Standardization
1.We need to know ‘observed’ deaths in Town A
2.We need to know the population in Town A in each age group
3.We choose age-specific deaths rates for a ‘standard’ population; in this case hypothetical country population

9. Indirect Standardization
Age group
Deaths ‘observed’: Town A
Population:
Town A
Country death rate per 1000/year (standard population)
Deaths ‘expected’: Town A
0-4
12400
1.50
5-14
26900
0.03
15-24
42000
0.32
25-34
32900
0.64
35-44
31700
2.34
45-54
27200
4.02
55-64
21600
6.69
65-74
18400
14.32
75-84
11300
78.30
85+
3200
180.20
Total
2520
227600

10. Indirect Standardization
1.We need to know ‘observed’ deaths in Town A
2.We need to know the population in Town A in each age group
3.We choose age-specific deaths rates for a ‘standard’ population
4.We calculate the numbers of deaths that would have occurred in Town A – expected deaths, in each age group, if the ‘standard’ population death rates had applied.

11. Indirect Standardization
•For that, we need to multiply the country rate (column 4) by the Town A population (column 3) in the same age group
For example, for the 0-4 age group: ퟏ.ퟓ풙ퟏퟐퟒퟎퟎ ퟏퟎퟎퟎ = 18.6
•Finally, add up all the age-specific expected deaths to obtain total number of expected deaths

12. Indirect Standardization
Age group
Deaths ‘observed’: Town A
Population:
Town A
Country death rate per 1000/year
(standard population)
Deaths ‘expected’: Town A
0-4
12400
1.50
18.60
5-14
26900
0.03
0.81
15-24
42000
0.32
13.44
25-34
32900
0.64
21.06
35-44
31700
2.34
74.18
45-54
27200
4.02
109.34
55-64
21600
6.69
144.50
65-74
18400
14.32
263.49
75-84
11300
78.30
884.79
85+
3200
180.20
576.64
Total
2520
227600
2106.85

13. Indirect Standardization
1.We need to know ‘observed’ deaths in Town A
2.We need to know the population in Town A in each age group
3.We choose age-specific deaths rates for a ‘standard’ population
4.We calculate the numbers of expected deaths in town A in each age group.
5.We can calculate the SMR now

14. Indirect Standardization
An SMR 120 means that, independently of the influence of the age distribution in Town A, the overall mortality in Town A is 20 per cent higher than country average (our ‘standard’ population).
SMR = 푻풐풕풂풍 풏풖풎풃풆풓 풐풇 풐풃풔풆풓풗풆풅 풅풆풂풕풉풔 푻풐풕풂풍 풏풖풎풃풆풓 풐풇 풆풙풑풆풄풕풆풅 풅풆풂풕풉풔 풙 ퟏퟎퟎ
SMR = ퟐퟓퟐퟎ ퟐퟏퟎퟔ.ퟖퟓ 풙 ퟏퟎퟎ=ퟏퟏퟗ.ퟔ ~ ퟏퟐퟎ

15. Indirect Standardization
–Interpretation of SMR
Independently of the influence of the age distribution, an SMR
1.of 100% means no difference between the overall mortality in the population of interest and in the standard population.
2.>100% means that the overall mortality in the population of interest is higher than in the standard population.
3.< 100% means that the overall mortality in the population of interest is lower than in the standard population.
15

16. Indirect Standardization
•To calculate SMR we need to know:
•Age-specific index population data
•Total number of deaths in the index population
•Age-specific deaths rates of the standard population
•SMR can be calculated if the numbers of deaths in each age group are not available
16

17. Indirect Standardization Now, we will calculate the SMR for Town B
Age group
Deaths ‘observed’: Town B
Population:
Town B
Country death rate per 1000/year (standard population)
Deaths ‘expected’: Town B
0-4
5200
1.50
7.80
5-14
15100
0.03
0.45
15-24
11300
0.32
3.62
25-34
11100
0.64
7.10
35-44
16600
2.34
38.84
45-54
15400
4.02
61.91
55-64
14900
6.69
99.68
65-74
12700
14.32
181.86
75-84
8800
78.30
689.04
85+
3100
180.20
558.62
Total
1626
114200
1648.93

18. Indirect Standardization
–We will calculate the SMR for Town B
An SMR 99 means that, independently of the influence of the age distribution in Town B, the overall mortality in Town B does not differ significantly (very close to 100) from that for the ‘standard’ population.
SMR = 푻풐풕풂풍 풏풖풎풃풆풓 풐풇 풐풃풔풆풓풗풆풅 풅풆풂풕풉풔 푻풐풕풂풍 풏풖풎풃풆풓 풐풇 풆풙풑풆풄풕풆풅 풅풆풂풕풉풔 풙 ퟏퟎퟎ
SMR = ퟏퟔퟐퟔ ퟏퟔퟒퟖ.ퟗퟑ 풙 ퟏퟎퟎ=ퟗퟖ.ퟔ ~ ퟗퟗ

19. Indirect Standardization
–Comparison of SMRs
We cannot compare SMRs between two populations, e.g. Town A and Town B - only to the standard population – because the age-specific rate have been applied to two different populations
What we can state, is that mortality in Town A is 20 per cent higher than the country average. For Town B, mortality does not differ significantly from the country level (very close to 100).
19

20. Direct Standardization
–Direct standardization allows direct comparison between two populations
20

21. Direct Standardization
–We will use population of Town A as the standard and standardize population of Town B against it
–We will first look at crude death rate for people aged 65 and over
Town A (standard)
No. of
population
Deaths observed
Age specific rate/1000
per year
65-74
18400
75-84
11300
85+
320
30020
297
9.89
Town B
No. of
population
Deaths observed
Age specific rate/1000
per year
65-74
12700
45
75-84
880
93
85+
310
220
13890
358
25.77

22. Direct Standardization
–Now, we will calculate age-specific rates for Town B
Town A (standard)
No. of
population
Deaths observed
Age specific rate/1000
per year
65-74
18400
75-84
11300
85+
320
30020
297
9.89
Town B
No. of
population
Deaths observed
Age specific rate/1000
per year
65-74
12700
45
3.54
75-84
880
93
105.68
85+
310
220
709.68
13890
358
25.77

23. Direct Standardization
–Standardize the Town B rate to the Town A:
1.Apply age-specific rates of Town B to the age-specific groups of Town A to calculate the expected numbers in each group
23
Age-specific rate for Town B
Town A (standard) population
Expected deaths for Town B
65-74
3.54
18400
65.20
75-84
105.68
11300
1194.20
85+
709.68
320
227.10
30020

24. Direct Standardization
–Standardize the Town B rate to the Town A:
2.Add up the expected deaths to obtain the total
3.Divide the total expected cases by the total Town A (standard ) population to obtain the age-standardized death rate (x 1,000)
24
Age-adjusted rate for Town B
Town A (standard) population
Expected deaths for Town B
65-74
3.54
18400
65.20
75-84
105.68
11300
1194.20
85+
709.68
320
227.10
49.52
30020
1486.50

25. Direct Standardization
–Interpretation
•Before standardization:
–Crude death rate in Town A for people aged 65 and over was 9.89 per 1000 per year
–Crude death rate in Town B for people aged 65 and over was 25.87 per 1000 per year (2.5 times higher than in Town A)
•After standardization of the population of Town B crude death rate to the population of Town A:
–Age-adjusted death rate in Town B for people aged 65 and over was 49.52 per 1000 per year (5 times higher than in Town A)
25

26. Direct Standardization
–To calculate age-adjusted deaths rates we need to know:
•Age-specific index population data
•Number of deaths in each age group in index population
•Age-specific standard population data
26

27. SUMMARY
Standardization is applicable for factors other than age (socio-economic status, race, area of residence)
Any rates can be standardized, e.g. incidence
Standardization is required to adjust rates for influence of factors, e.g. age, which could have impact on the comparison of those rates
27

28. SUMMARY
There are two methods: indirect and direct standardization
Indirect standardization applies age-specific rates from the standard population to the numbers of people in each age group in the index population
Direct standardization applies age-specific rates from the index population to the numbers of people in each age group of a standard population
28

29. SUMMARY
Indirect standardization (calculation of SMR) does not require age-specific rates in the index population
Indirect standardization does not allow direct comparison between SMRs
Indirect standardization is more precise
29