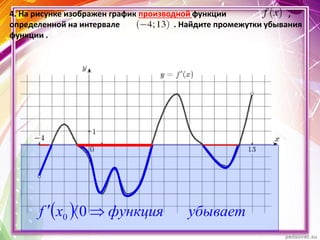
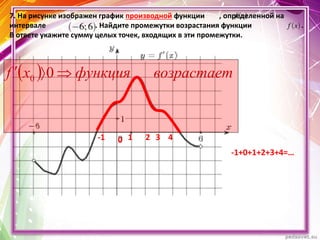
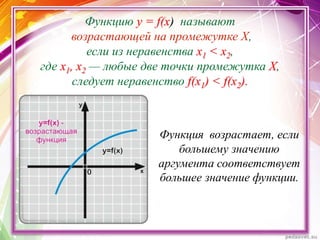
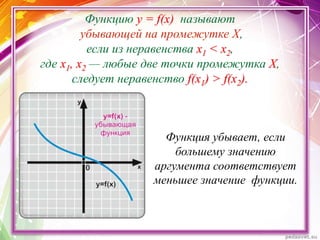
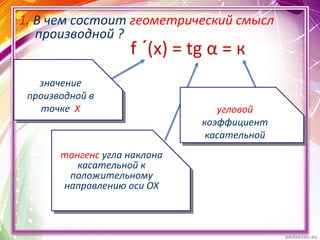
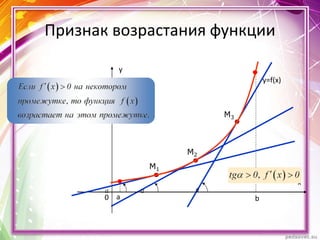
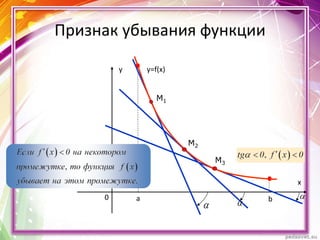
Документ описывает применение производной для исследования монотонности функций y = f(x). Он определяет возрастающие и убывающие функции на интервалах и включает правила нахождения интервалов монотонности. Приведены примеры нахождения промежутков возрастания и убывания функции с использованием её производной.

1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ.
ИССЛЕДОВАНИЕ ФУНКЦИИ

2. Функцию у = f(x) называют
возрастающей на промежутке X,
если из неравенства х1 < х2,
где х1, х2 — любые две точки промежутка X,
следует неравенство f(x1) < f(x2).
Функция возрастает, если
большему значению
аргумента соответствует
большее значение функции.

3. Функцию у = f(x) называют
убывающей на промежутке X,
если из неравенства х1 < х2,
где х1, х2 — любые две точки промежутка X,
следует неравенство f(x1) > f(x2).
Функция убывает, если
большему значению
аргумента соответствует
меньшее значение функции.

4. 1. В чем состоит геометрический смысл
производной ?
значение
производной в
точке Х
тангенс угла наклона
касательной к
положительному
направлению оси ОХ
угловой
коэффициент
касательной
f ´(x) = tg α = к

5. а b
x
0
y
Признак возрастания функции
y=f(x)
 
M3
M1
M2

6. а b
x
0
y
Признак убывания функции
y=f(x)
 

M3
M1
M2

7. Правило нахождения интервалов
монотонности
1) Вычисляем производную f `(x) данной функции f(x).
2) Находим точки, в которых f `(x) = 0 или не
существует. Эти точки называются критическими
для функции f(x).
3) Критическими точками область определения
функции f(x) разбивается на интервалы, на каждом из
которых производная f `(x) сохраняет свой знак. Эти
интервалы будут интервалами монотонности.
4) Определим знак f `(x) на каждом из найденных
интервалов. Если на рассматриваемом интервале
f `(x) ≥ 0, то на этом интервале f(x) возрастает, если же
f `(x) ≤ 0, то на таком интервале f(x) убывает.

8. f(x)
f/(x)
x
y = f /(x)4
3
2
1
-1
-2
-3
-4
-5
y
x
+– –++
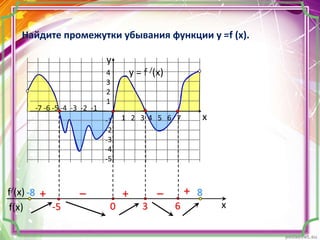
Найдите промежутки возрастания функции у =f (x).
В точках –5, 0, 3 и 6
функция непрерывна,
поэтому при записи
промежутков возрастания
эти точки включаем.
630
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-5
Ответ:
(–8; –5], [ 0; 3], [ 6; 8)
-8 8

9. f(x)
f/(x)
x
y = f /(x)4
3
2
1
-1
-2
-3
-4
-5
y
x
+– –++
Найдите промежутки убывания функции у =f (x).
630
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-5
-8 8

10. 4. На рисунке изображен график производной функции ,
определенной на интервале . Найдите промежутки убывания
функции .
  убываетфункцияxf  00

11. 7. На рисунке изображен график производной функции , определенной на
интервале . Найдите промежутки возрастания функции .
В ответе укажите сумму целых точек, входящих в эти промежутки.
  возрастаетфункцияxf  00
-1 40 1 2 3
-1+0+1+2+3+4=…