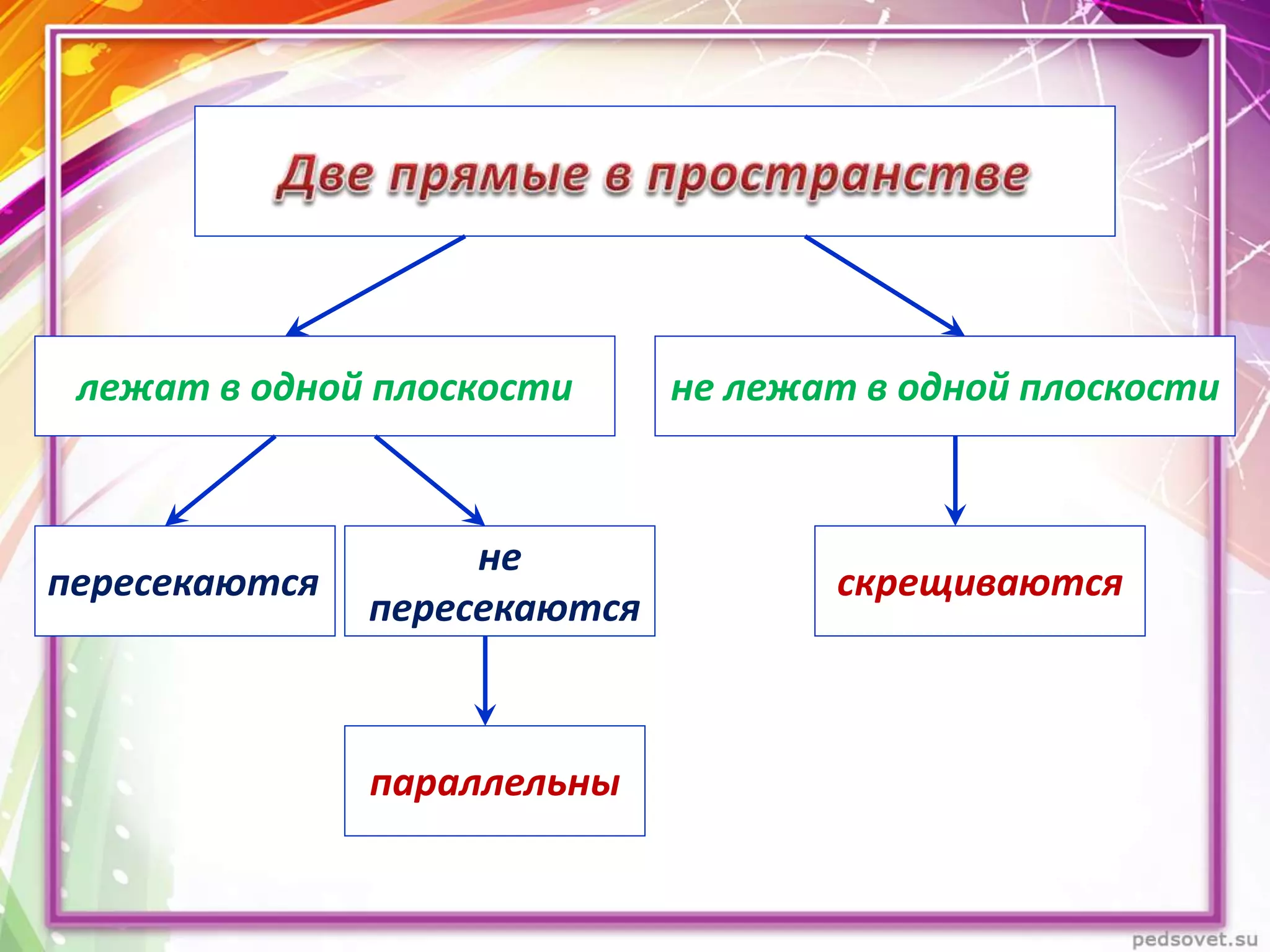
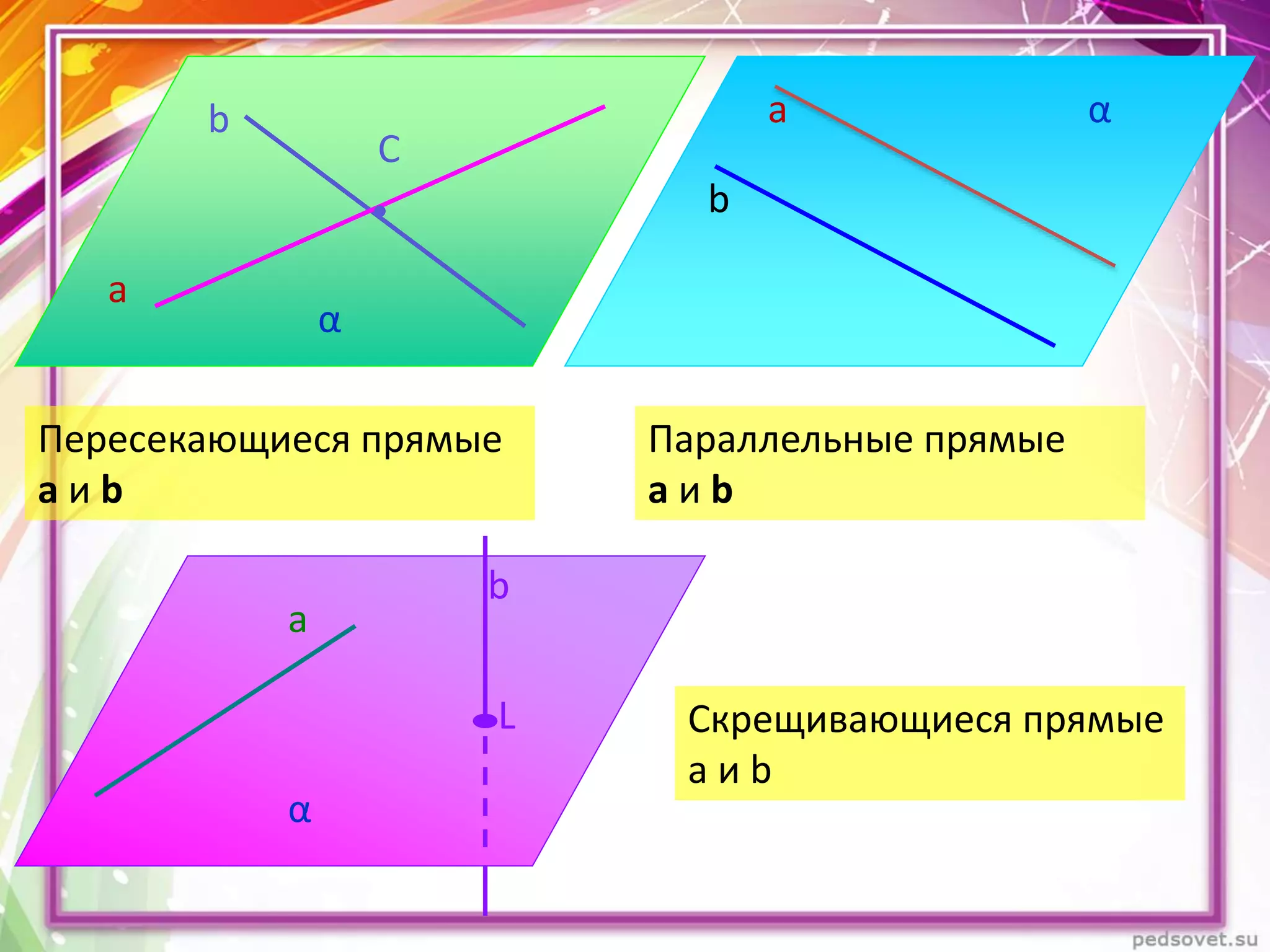
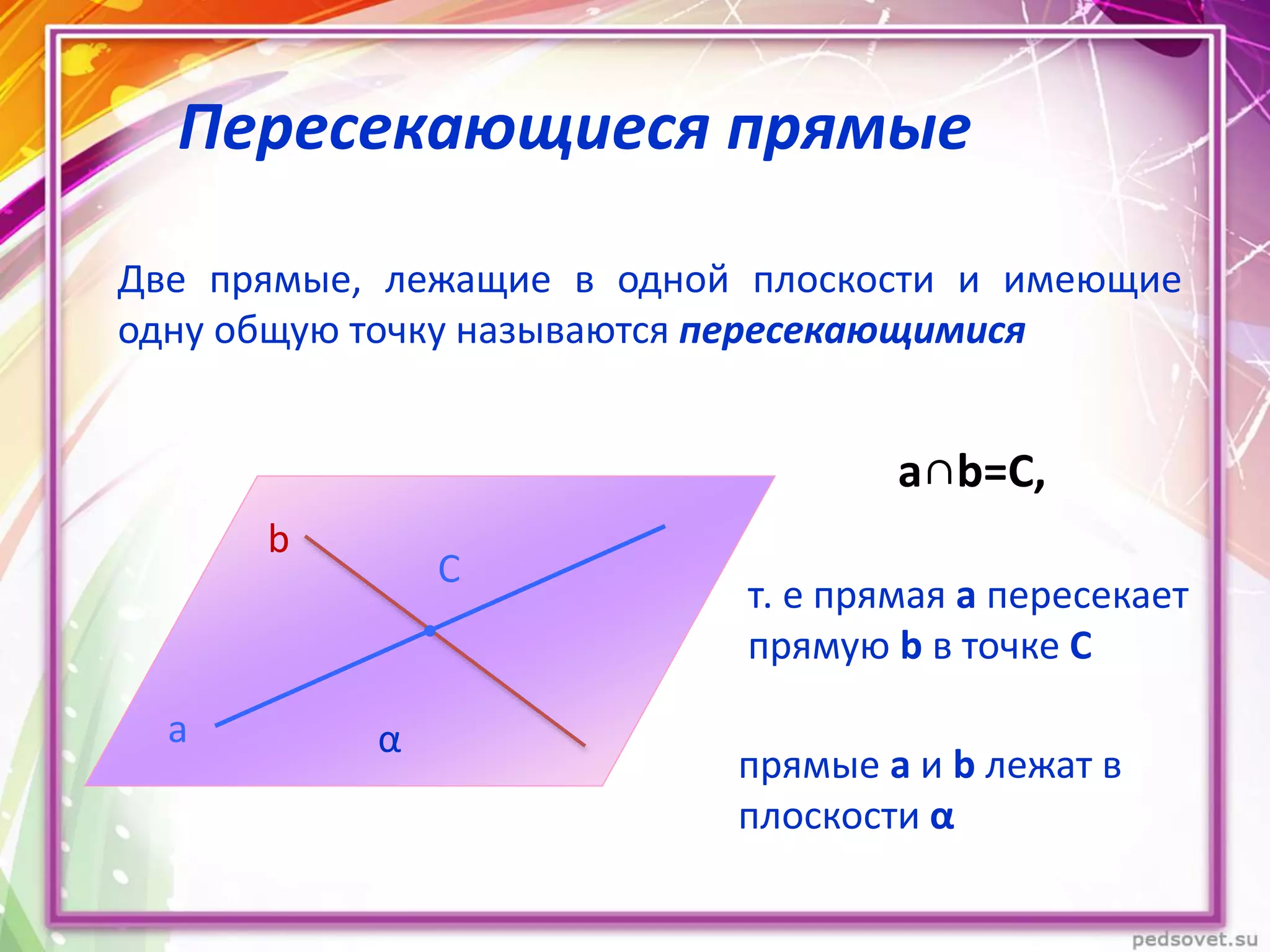
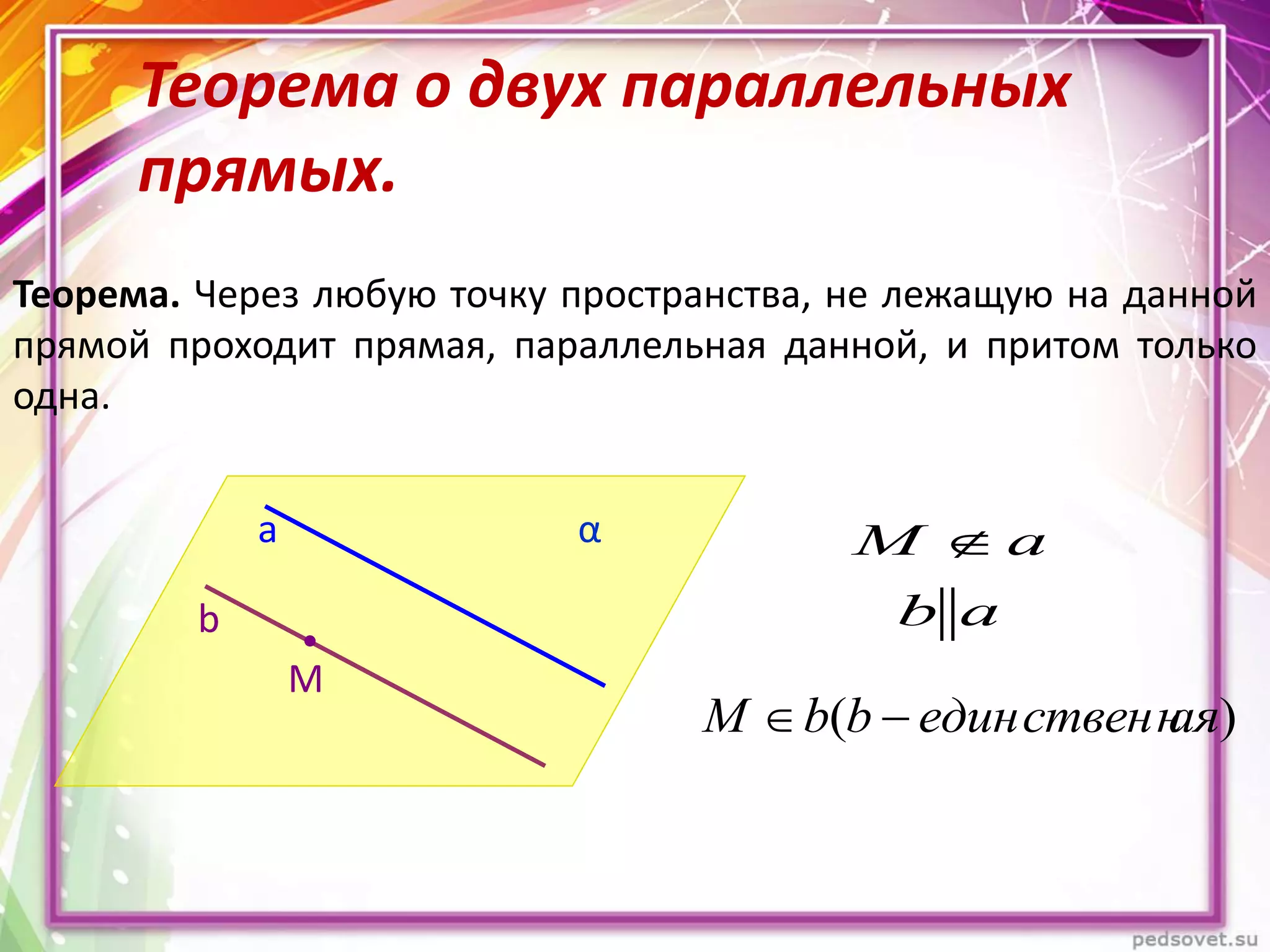
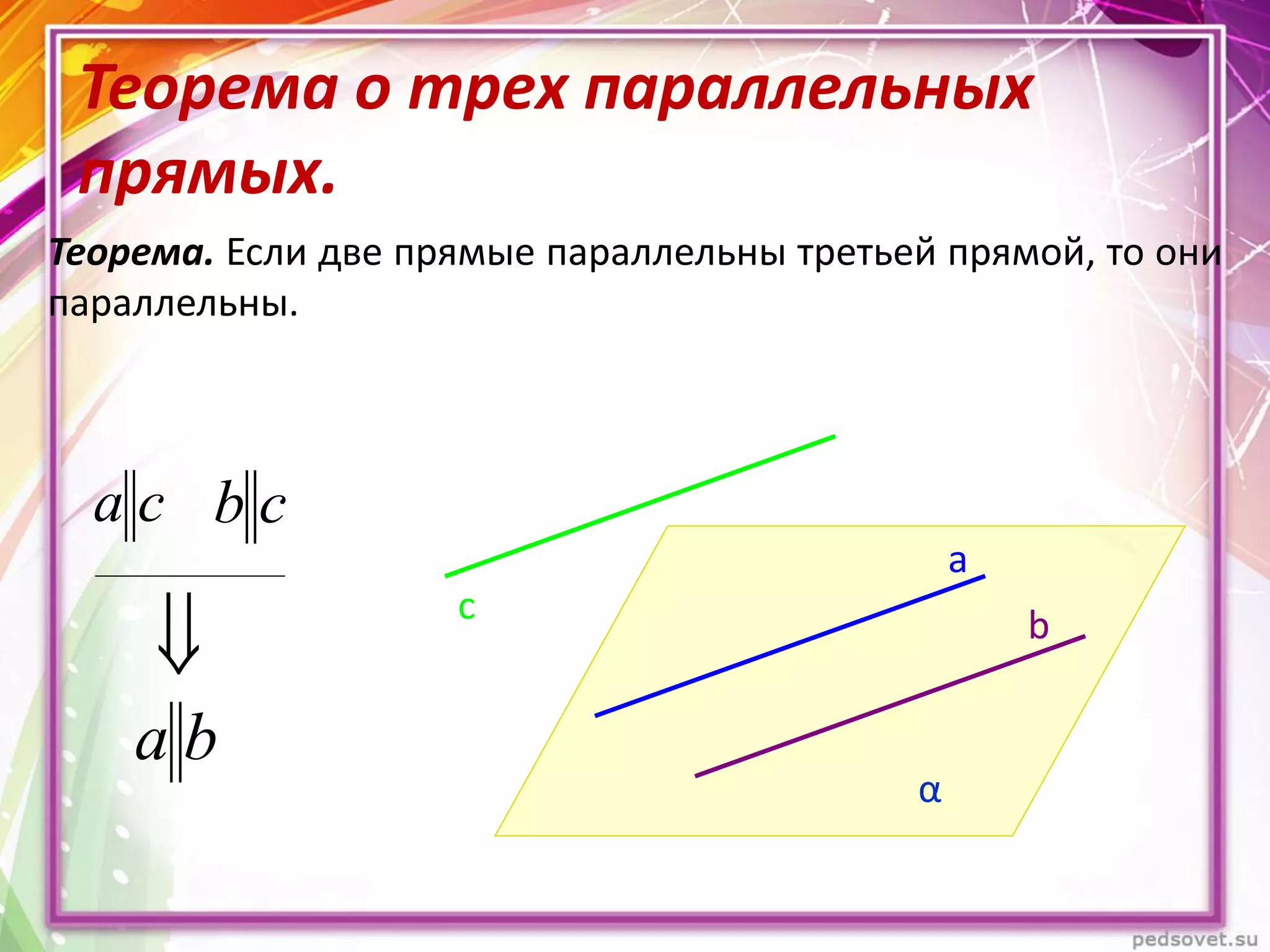
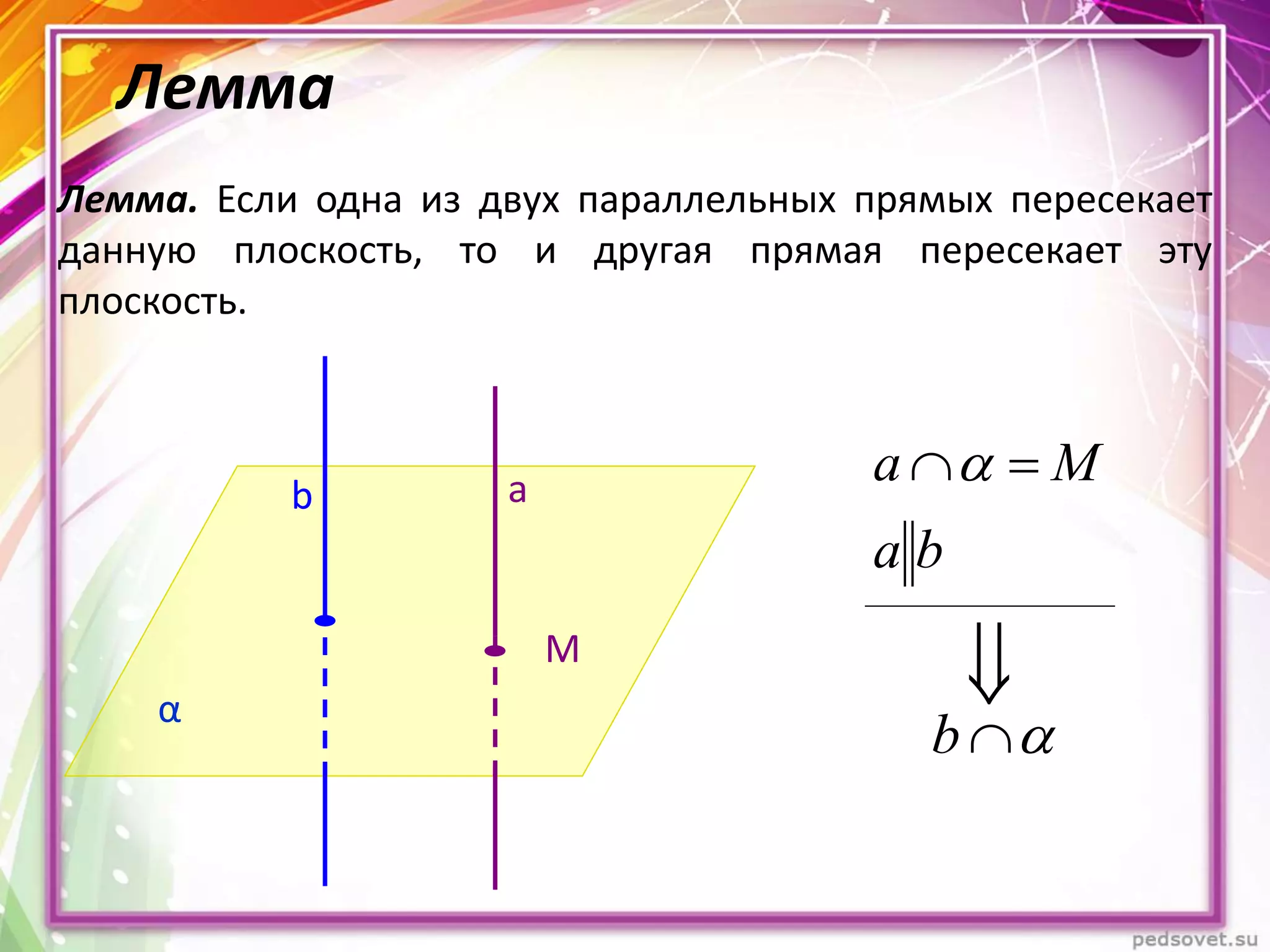
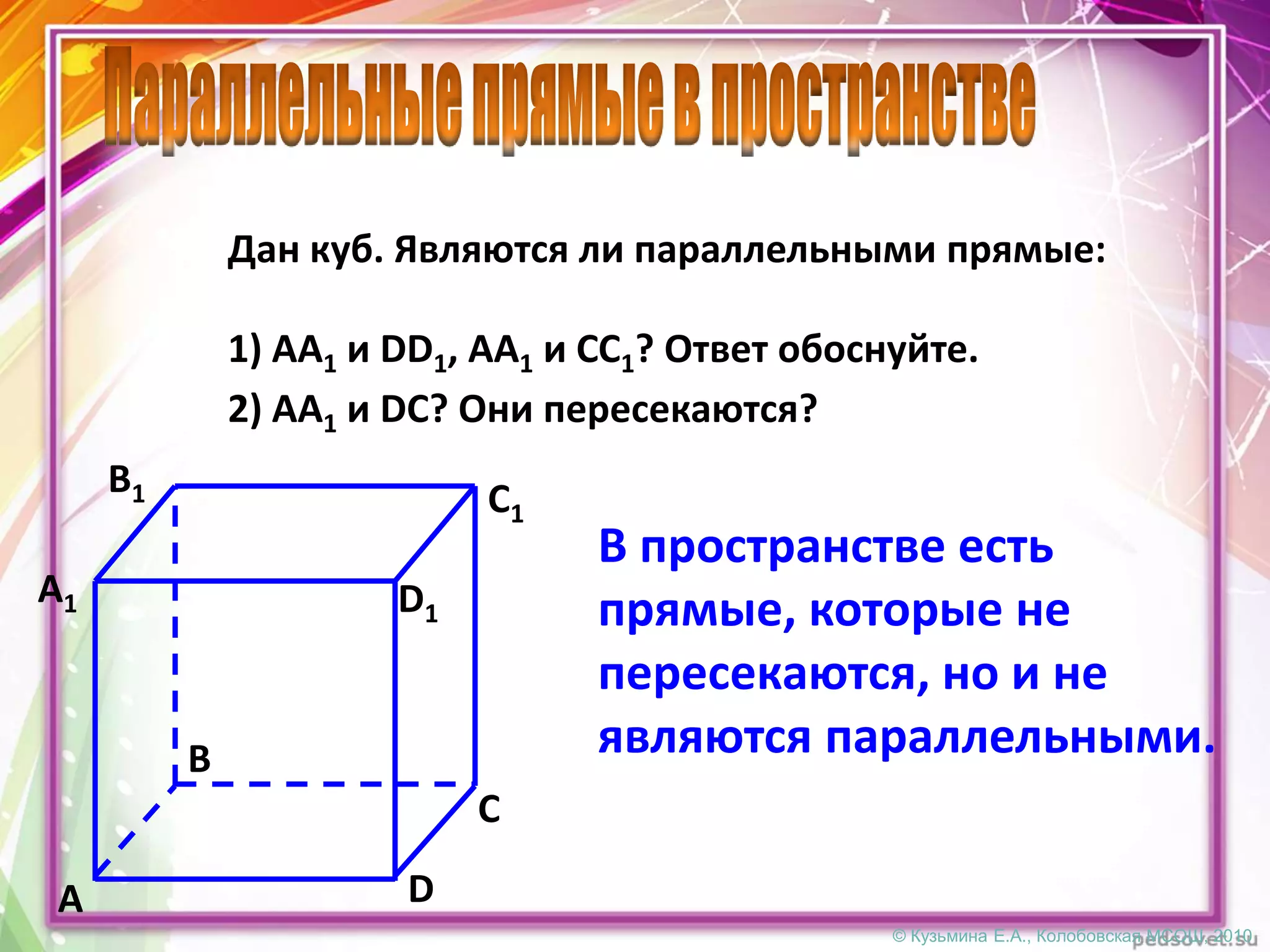
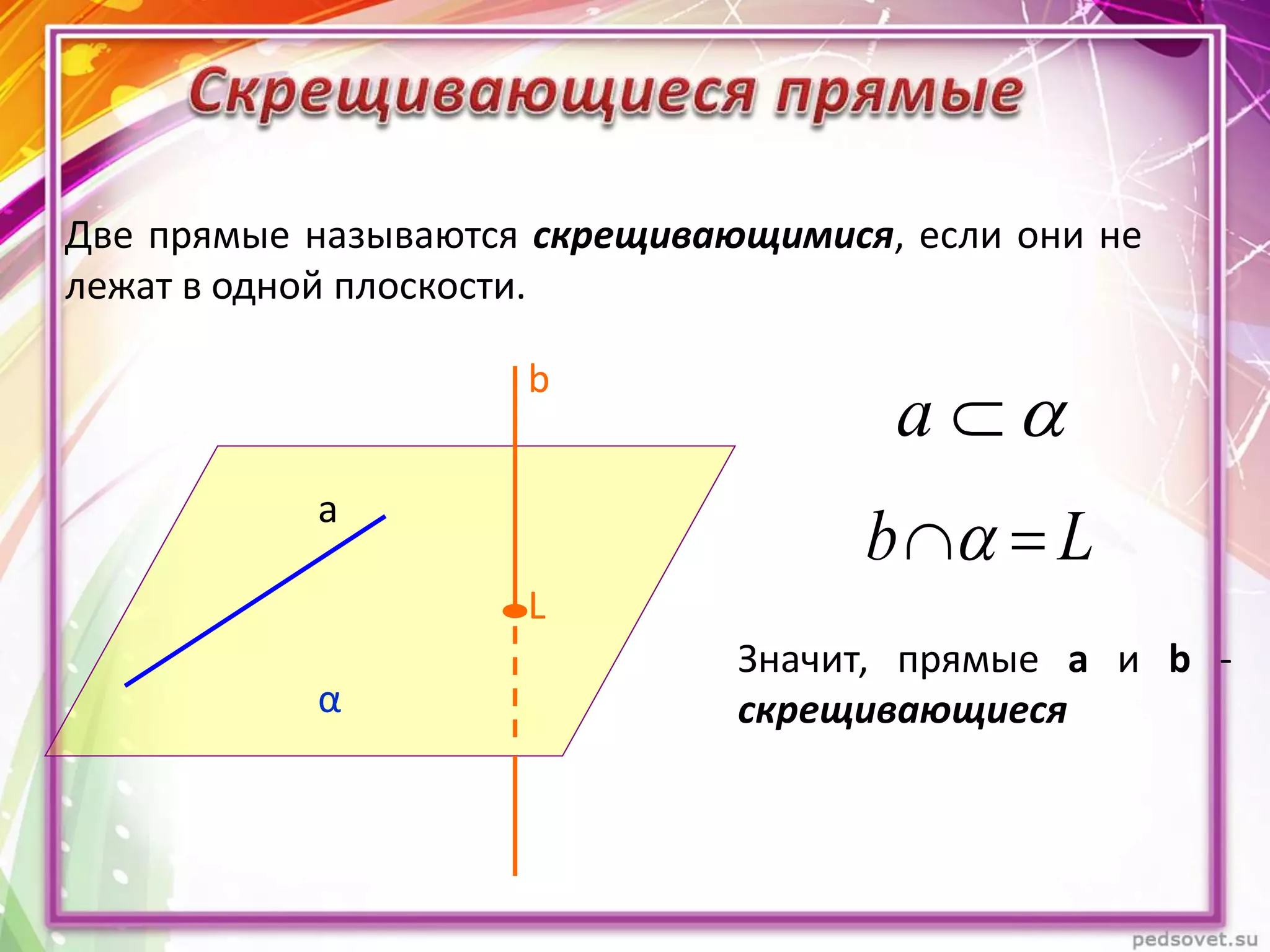
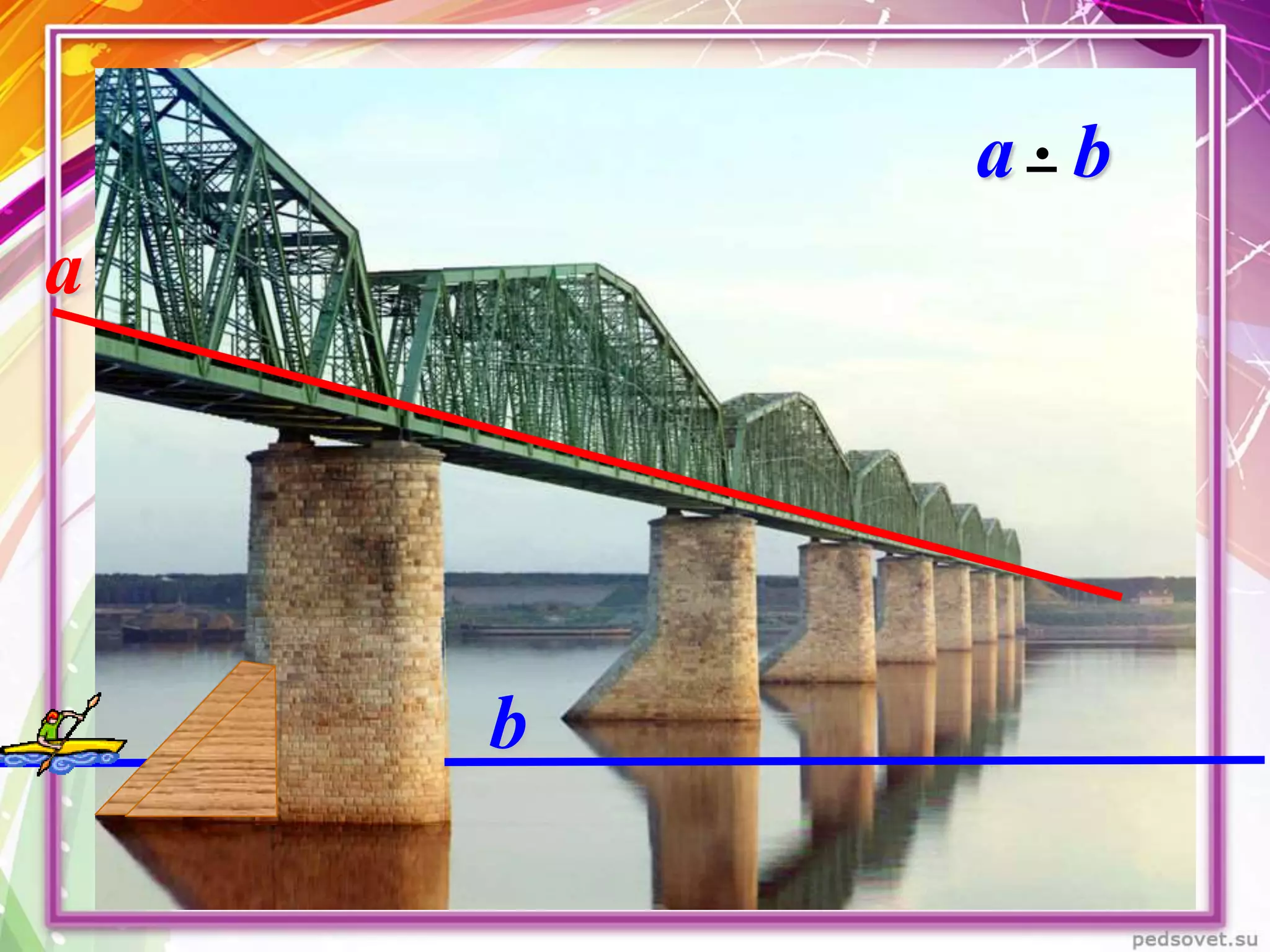
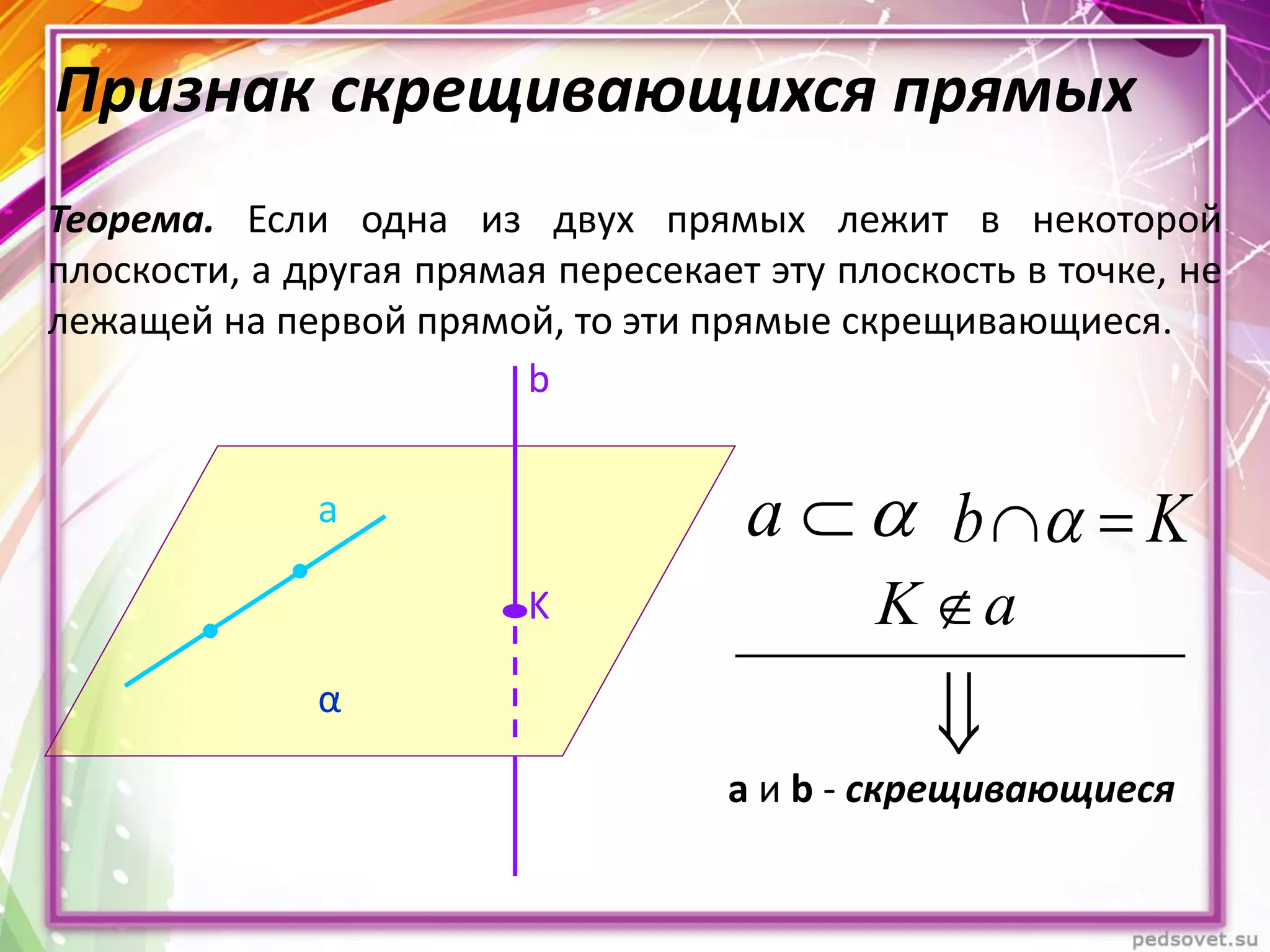
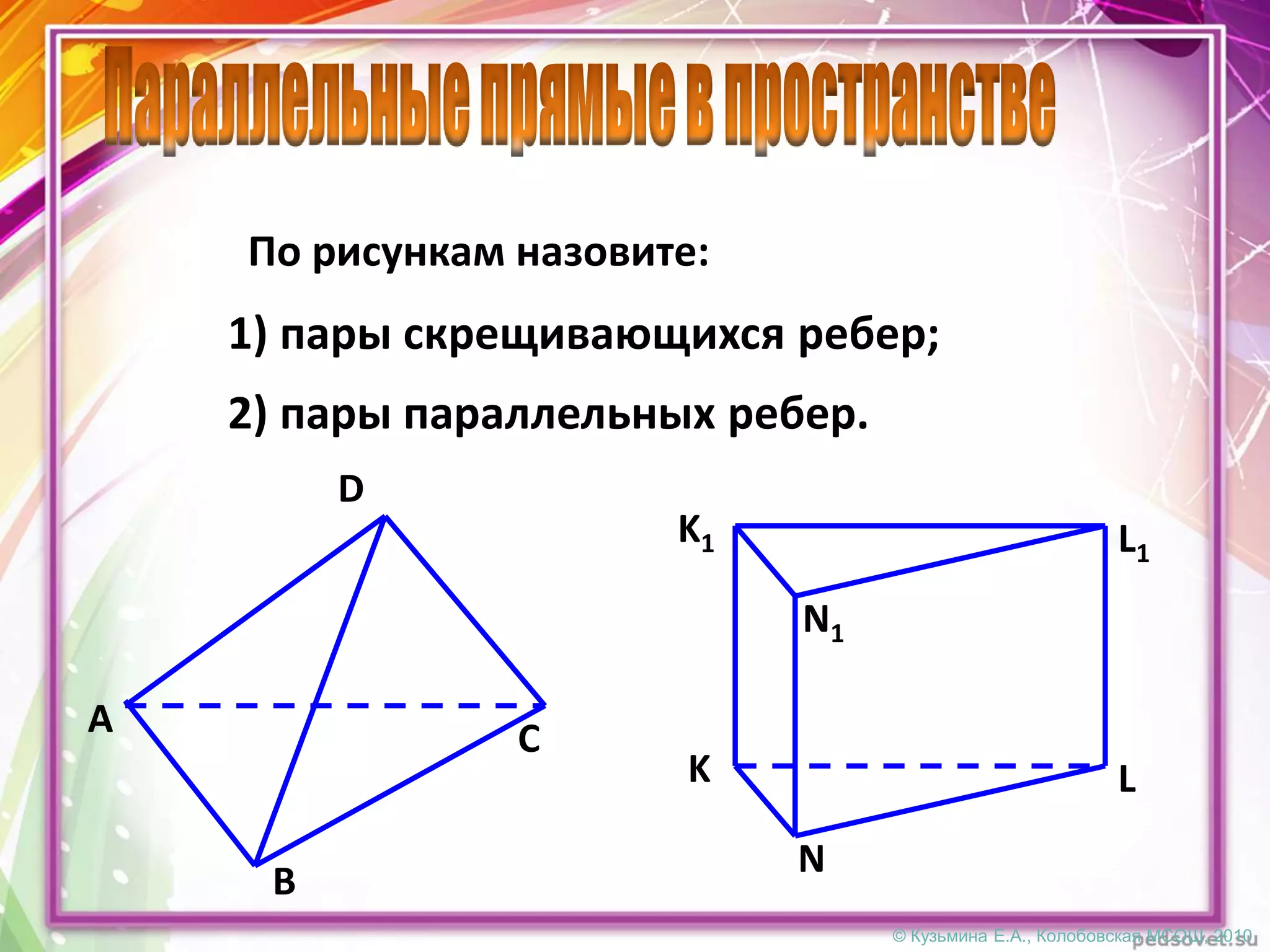
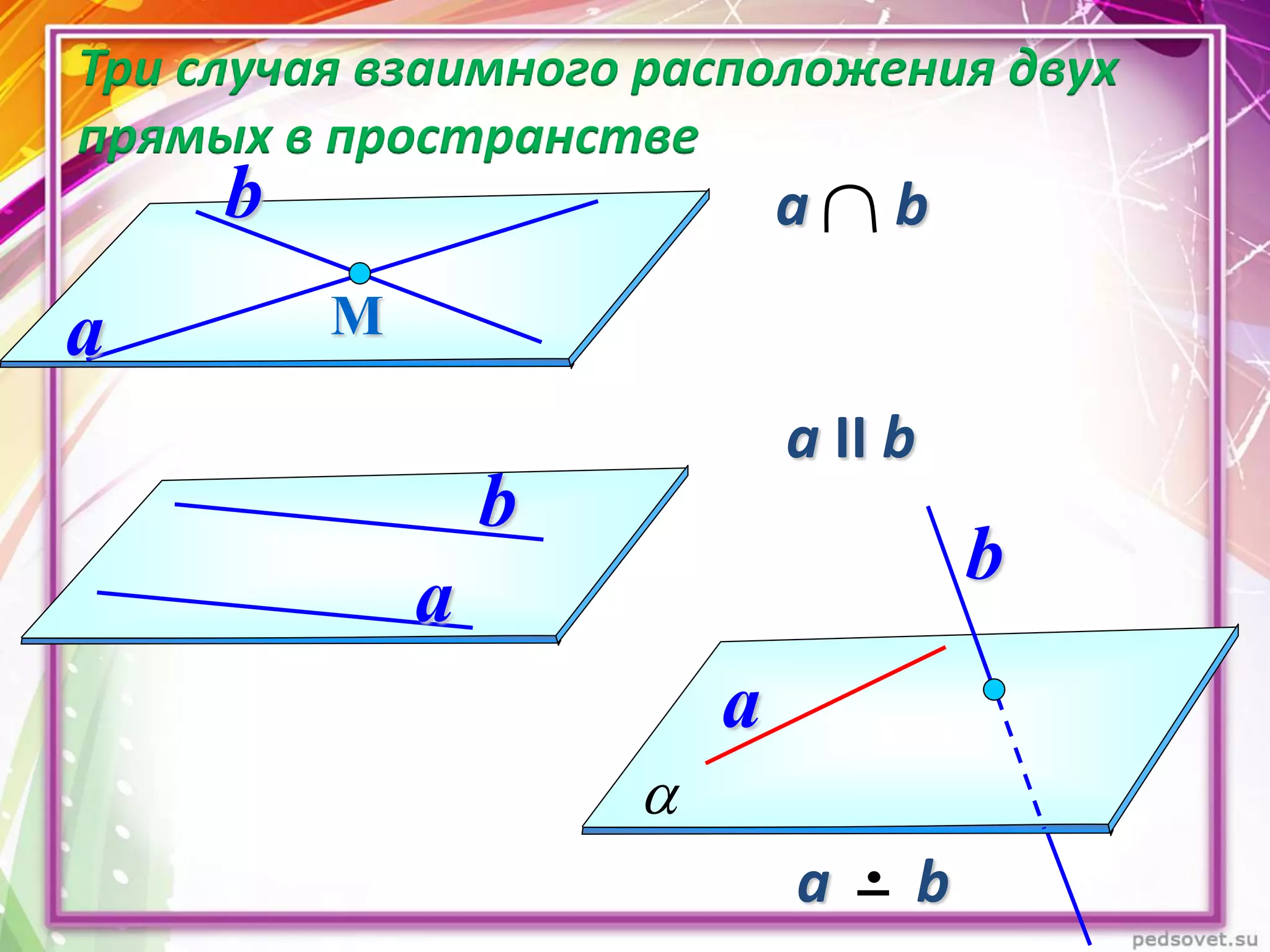
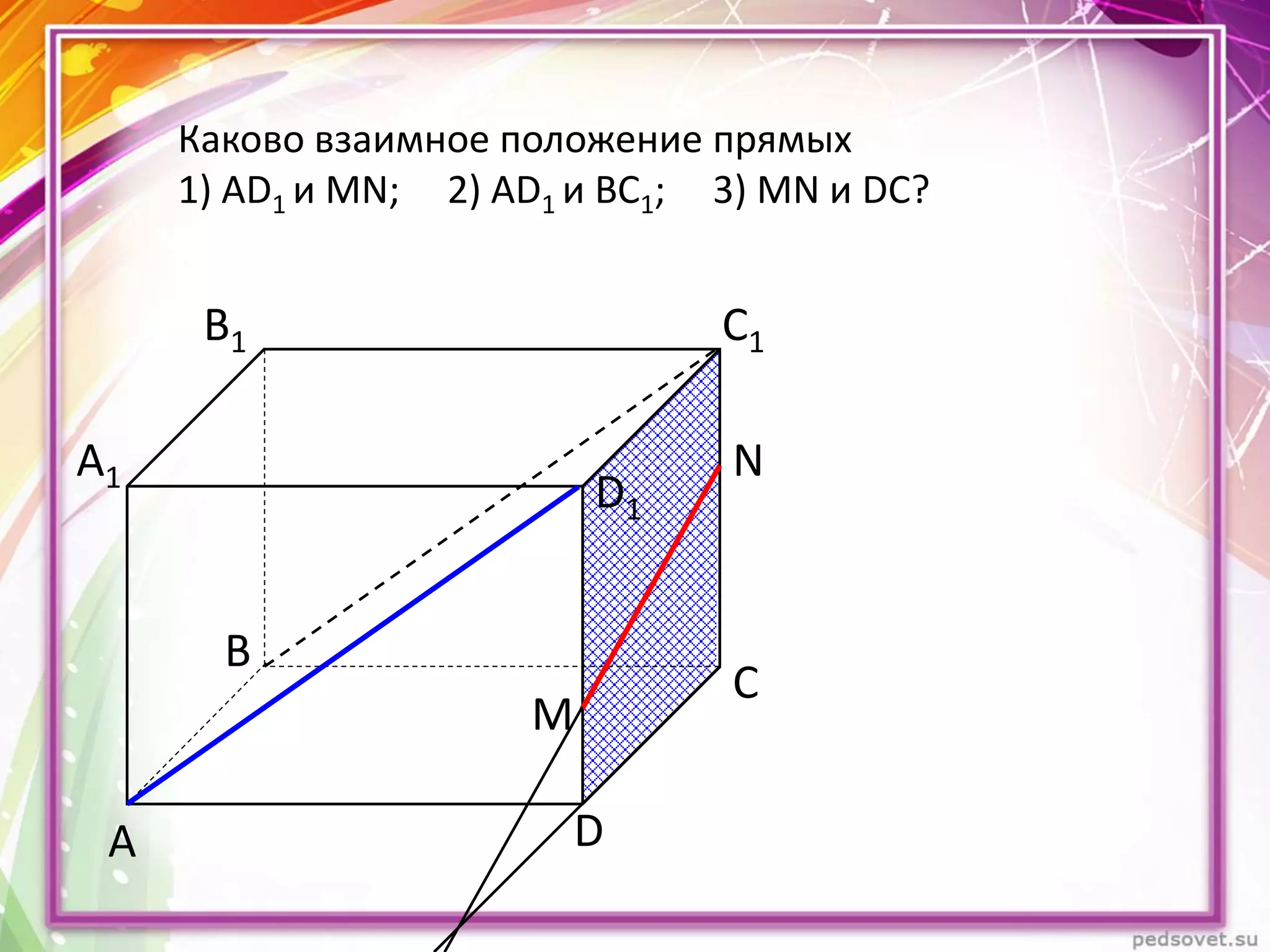
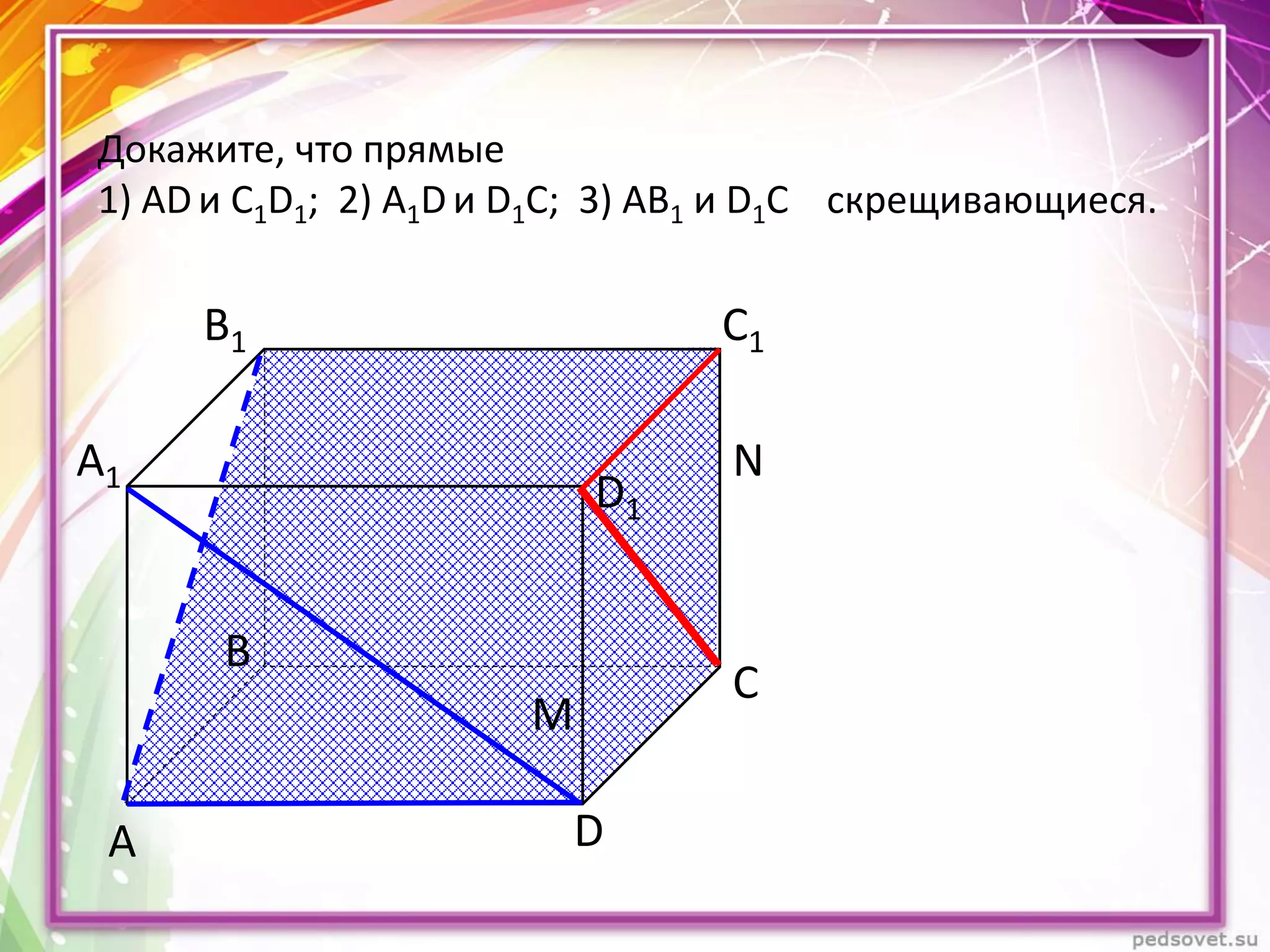
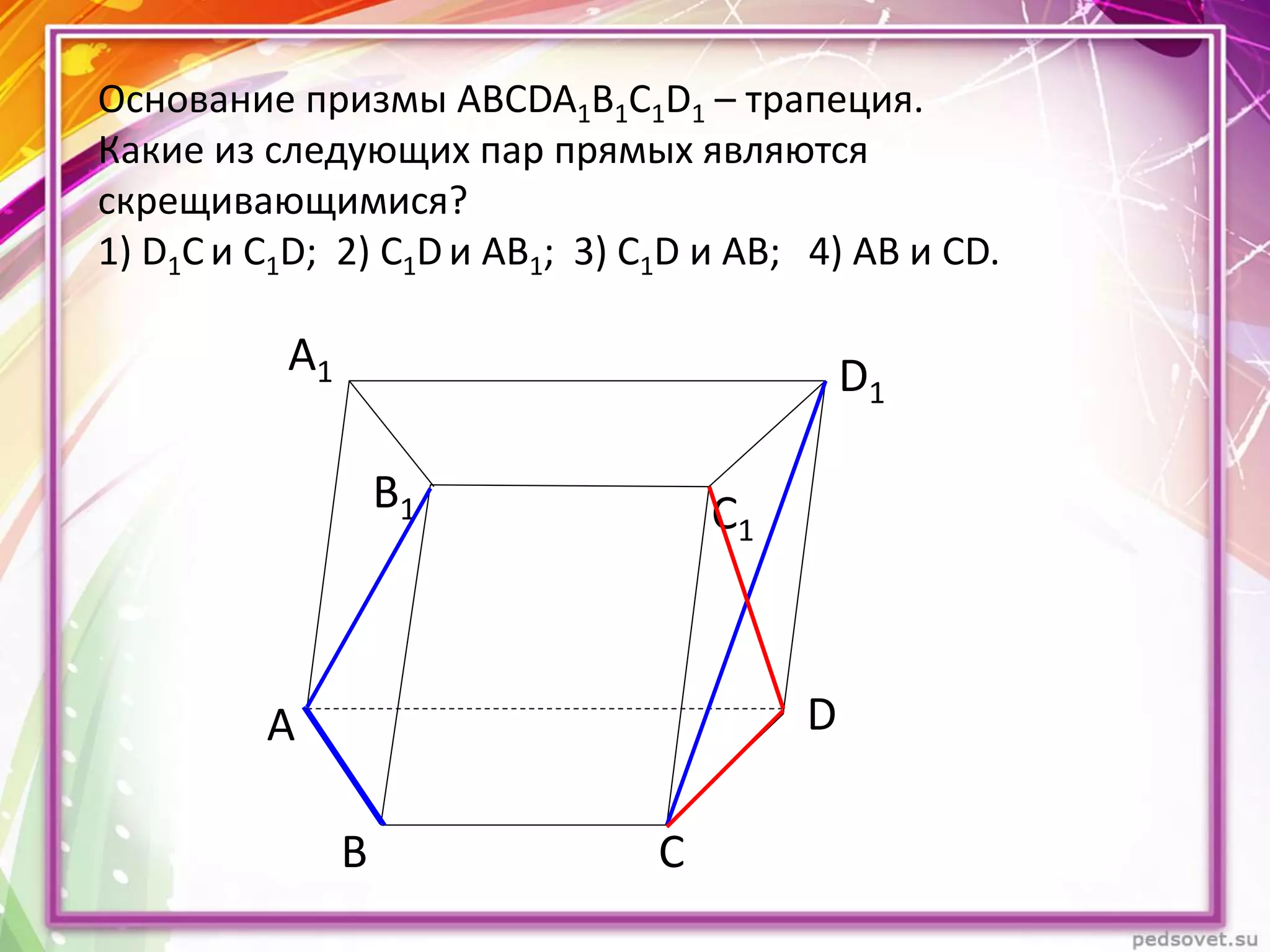
Документ описывает различные взаиморасположения прямых в пространстве, включая пересекающиеся, параллельные и скрещивающиеся прямые. Приводятся теоремы и леммы, касающиеся данных типов прямых, а также примеры и задачи для иллюстрации. Кроме того, рассматриваются визуальные представления и пояснения к понятиям, связанным с параллельными и скрещивающимися прямыми.

2. лежат в одной плоскости не лежат в одной плоскости
пересекаются
не
пересекаются
скрещиваются
параллельны

3. C
b
α
b
a α
Пересекающиеся прямые
a и b
Параллельные прямые
а и b
a
b
L
α
Скрещивающиеся прямые
а и b
а

4. Пересекающиеся прямые
Две прямые, лежащие в одной плоскости и имеющие
одну общую точку называются пересекающимися
C
b
a α
a∩b=C,
т. е прямая а пересекает
прямую b в точке С
прямые а и b лежат в
плоскости α

5. Параллельные прямые
Две прямые в пространстве называются параллельными,
если они лежат в одной плоскости и не пересекаются.
b
a α
a ‫׀׀‬ b,
т.е прямая а
параллельна прямой b
прямые а и b лежат в
плоскости α

6. Теорема о двух параллельных
прямых.
Теорема. Через любую точку пространства, не лежащую на данной
прямой проходит прямая, параллельная данной, и притом только
одна.
b
a α
М
аb
аМ 
)( аяединственнbbМ 

7. Теорема о трех параллельных
прямых.
Теорема. Если две прямые параллельны третьей прямой, то они
параллельны.
b
a
α
с
ca cb

ba

8. Лемма
Лемма. Если одна из двух параллельных прямых пересекает
данную плоскость, то и другая прямая пересекает эту
плоскость.
ab
М
α
ba
Mа 

b

9. © Кузьмина Е.А., Колобовская МСОШ, 2010
Дан куб. Являются ли параллельными прямые:
D
C
A
B
D1
C1
A1
B1
1) АА1 и DD1, АА1 и СС1? Ответ обоснуйте.
2) АА1 и DС? Они пересекаются?
В пространстве есть
прямые, которые не
пересекаются, но и не
являются параллельными.

10. Две прямые называются скрещивающимися, если они не
лежат в одной плоскости.
a
b
L
α
Lb 
a
Значит, прямые а и b -
скрещивающиеся

11. Наглядное представление о скрещивающихся прямых дают две
дороги, одна из которых проходит по эстакаде, а другая под
эстакадой.

12. a
b
a b

13. Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.

14. Признак скрещивающихся прямых
Теорема. Если одна из двух прямых лежит в некоторой
плоскости, а другая прямая пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти прямые скрещивающиеся.
a
b
K
α
Kb a
aK 

а и b - скрещивающиеся

15. © Кузьмина Е.А., Колобовская МСОШ, 2010
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных ребер.
D
CA
B
K L
N
K1 L1
N1

16. а II b

Три случая взаимного расположения двух
прямых в пространстве
а b
Мa
b
a
b
a
b
а b

17. А D
С
В
B1 С1
D1
А1
Каково взаимное положение прямых
1) AD1 и МN; 2) AD1 и ВС1; 3) МN и DC?
N
M

18. А D
С
В
B1 С1
D1
А1
Докажите, что прямые
1) AD и C1D1; 2) A1Dи D1C; 3) AB1 и D1C скрещивающиеся.
N
M

19. А D
СВ
B1 С1
D1
А1
Основание призмы АВСDA1B1C1D1 – трапеция.
Какие из следующих пар прямых являются
скрещивающимися?
1) D1C и C1D; 2) C1D и AB1; 3) C1D и AB; 4) AB и CD.