Документ описывает программу дистанционного образования, целью которой является обеспечение равного доступа учащихся к знаниям и возможность изучения материала в удобном темпе. Программа включает в себя изучение производной функции и навыков самооценки через различные задания и примеры. Она также помогает развивать интерес к предмету, предоставляя учащимся практические упражнения и теоретические знания.

2. Программа дистанционного образования
направлена на создание условий для доступа к
мировым культурно-исторических достижений
человечества и реализацию права каждого
учащегося на одинаковые возможности для
получения образования, независимо от места
проживания, состояния здоровья и пр. Она дает
возможность каждому школьнику выучить
материал темы и выполнять задания в том темпе,
который отвечает его способностям

3. Предложенные задания помогут тебе
открыть для себя много нового и
интересного. Будь уверен. Ты блестяще
справишься с этой программой.

4. • Овладеть новыми понятиями: предел функциив
точке, дифференцирование, правила
дифференцирования, монотонность, экстремум;
• Закрепить навыки дифференцирования в процессе
решения примеров;
• Отработать навыки нахождения производной и ее
применение при решении задач, предложенных
для самостоятельного решения;
• Развивать навыки самооценки и самоконтроля;
• Поддерживать заинтересованность предметом.

5. Урок № 1 Урок № 2
Урок № 3
Урок № 4 Урок № 5

6. Теория
Практика
Самостоятельная
работа

7. Определение: Производная функции – это предел
отношения приращения аргумента к приращению
функции, при стремлении приращения аргумента к
нулю, т.е.
Определение: Если функция дифференцируема в
каждой точке некоторого интервала , то она
называется дифференцируемой на этом интервале.
Определение: Если функция в точке х0
дифференцируема, то она непрерывна
в этой точке.

9. 1. Сумма(разность) двух функций
2. Произведение двух функций
3. Частное двух функций
4. Сложная функция
К содержанию урока

11. Решение
Решение А Решение Б

12. № 2.Найдите производную функции
a) б)
Решение
а)
б)

13. Реши сам
№1. Вычислить производную функции
в точке
Подсказка Решение
№2. Используя определение производной,
найти f '(x), если а) f(x)= 3x+2
б)
Подсказка Решение

14. Уровень 1 Уровень 2

15. Теория
Практика
Самостоятельная
работа

16. Закон движения
Закон равномерного движения
Скорость равномерного движения
Закон равноускоренного движения
Скорость равноускоренного движения
Ускорение равноускоренного движения
К содержанию

17. Угловая скорость – производная от угла поворота, т.е.
Угловое ускорение – производная от угловой скорости, т.е.
Сила тока – производная от количества электричества, т.е.
Мощность – производная от работы, т.е.
Теплоемкость – производная от количества теплоты, т.е.
Производительность труда – производная
от объема продукции, т.е.
Мгновенная скорость – производная от пути
в момент времени t, т.е.

18. Угловой коэффициент касательной,
проведенной к графику функции в точке
, равен
Уравнение касательной к графику функции
в точке имеет вид:
К содержанию

19. На графике функции найдите
точку, в которой касательная параллельна прямой
Решение
Т.к. касательная параллельна прямой , то
угловой коэффициент касательной равен 3. Значит,
когда . Получим:
Ответ: (2;3)
К содержанию

20. При движении тела по прямой его скорость v (м/с)
меняется по закону , где
t - время движения в секундах. Найдите ускорение
(м/ с2) через 2 секунды после начала движения.
Решение.
Т.к. а(t)=v′(t), то a(t) = t4 − 3t2 + 1.
a(2) = 16 − 12 + 1= 5 (м/с2)
Ответ: 5 м/c2.
К содержанию

21. Количество теплоты , которое необходимо для
нагревания воды массой 1 кг от 0°С до температуры
t°С(0°≤t≤95°), приближенно можно определить по
формуле:
Решение

22. Составьте уравнение касательной к графику
функции в его точке пересечения с
осью ординат.
Решение.
Очевидно, что абсцисса точки касания . Тогда
. Получим:
Подставим полученные числовые значения в общее
уравнение касательной
Получим:
Ответ:
К содержанию

23. Точка движется по закону S(t)=1+3t. Найти
среднюю скорость движения за
промежуток времени от t=1 до t=4.
Решение.
Ответ: средняя скорость равна 3

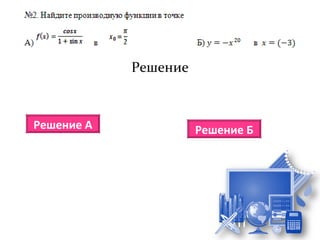
24. №1. Найти мгновенную скорость движения точки, если
закон ее движения s(t) задан формулой
Подсказка Решение
№2. Точка вращается вокруг оси по закону .
Найдите угловую скорость точки в момент времени t.
Подсказка Решение
№3. Объем продукции V мастерской, производящей
елочные украшения, в течении дня выражается
зависимостью ,
где t [1;3]. Вычислите производительность
труда мастерской в течении каждого часа.
Подсказка Решение

25. Уровень 1 Уровень 2

26. Теория
Практика
Самостоятельная
работа

27. Если на промежутке, то функция
возрастает на этом промежутке .
Если на промежутке, то функция
убывает на этом промежутке
Если на промежутке, то функция
на этом промежутке постоянна.
Внутренние точки области определения
функции, в которых ее производная равна нулю
или не существует, называются критическими
точками функциями.
Точки, в которых производная равна нулю
называются стационарными

28. 1. Найти
2. Найти
3. Найти критические точки, т. е. точки, в которых
или не существует.
4. Расположить на координатной оси и
стационарные точки. Определить знак
полученных интервалов.
5. Если производная положительна на интервале
, то на этом интервале функция возрастает.
Если производная отрицательна на интервале
, то на этом интервале функция убывает.
6. Записать ответ.

29. 1. Найти D ( f )
2. Найти f '( x )
3. Найти критические точки, т.е. точки, в которых
производная функции равна нулю или не
существует
4. Расположить критические точки и на
координатной оси. Определить знаки полученных
промежутков.
5. Если при переходе через точку производная меняет
знак с «-» на «+», то в этой точке функция имеет
минимум, если с «+» на «-», то в этой точке функция
имеет максимум.
6. Записать ответ
Замечание: если функция исследуется на экстремум на
отрезке, то нужно проверить на наличие
экстремальных точек концы отрезка.

30. Исследуйте функцию на возрастание, убывание и
экстремум.
Решение
Исследуем функцию на монотонность.
1)
2) =
=

31. 3)
4)
х
0 1 2
5) Функция возрастает на промежутках и
Функция убывает на промежутке и
Найдем экстремум функции, х=0 – точка
максимума, х=2 – точка минимума.

32. Найдите критические точки функции
Решение.
в ;
не существует в и
Ответ: 0; 1,5; 3

33. № 1. Используя график функции, найти ее точки экстремума,
а
также наибольшее и наименьшее значение.
Решение

34. №2. Найдите стационарные точки функции
Подсказка Решение
№3. Найдите промежутки возрастания и убывания функции
Подсказка Решение
№4. Найдите точки экстремума функции
Подсказка Решение

35. Уровень 1 Уровень 2

36. Теория
Практика
Самостоятельная
работа

37. 1. Найти область определения функции
2. Исследовать функцию на четность -
нечетность
3. Найти нули функции, решив уравнение
4. Исследовать функцию на монотонность и
экстремум.
5. Вычислить значение функции в точках
экстремума

38. Постройте график функции
Решение
1. Область определения - вся числовая прямая
2. Исследуем на четность- нечетность
Значит, функция является нечетной
3. Найдем нули функции
нули функция имеет в точках

39. 4. Исследуем функцию на монотонность и
экстремум
;
-1 1
5. Найдем значение функции в критических точках
В точке х= -1 функция имеет максимум, в точке х=1
функция имеет минимум.

40. К содержанию

41. Построить график функции
Решение
1. Область определения - вся числовая
прямая
2. Исследуем функцию на четность.
, т.е. функция не является
четной
, т.е. функция не является
нечетной

42. 3. Найдем нули функции
; ;
нули функции
4. Исследуем функцию на монотонность и экстремум
5. Найдем значение функции в критических точках
;

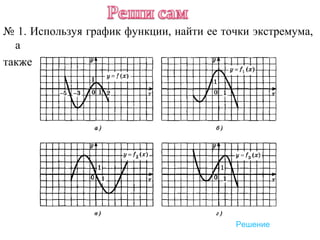
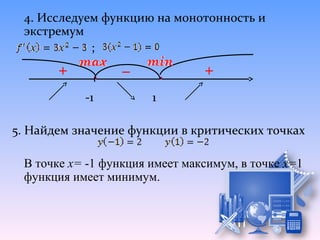
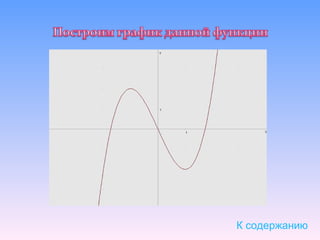
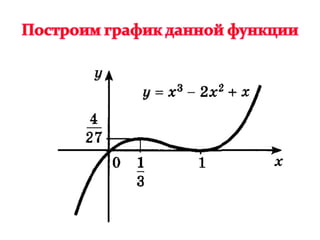
44. №1. Построить график функции на отрезке
[-1;2]
Подсказка Решение
№ 2. Построить график функции
Подсказка Решение

45. Уровень 1 Уровень 2

46. Теория
Практика
Контрольная
работа

47. Если на концах промежутка возрастающая
функция принимает значения разных знаков,
то на этом промежутке график функции
пересекает ось Ох в одной точке.
Следовательно, на этом промежутке
имеет один корень.

48. Найдите наименьший член последовательности
Решение
Для того, чтобы решить задачу нужно найти минимальное
значение функции .Найдем производную данной
функции . Решим уравнение . Получили
3,5
Т.к. в точке n=3,5 производная функции меняет знак с «-» на «+»,
то в этой точке наблюдается минимум. Найдем значение
функции в этой точке .
Т.е. Наименьший член последовательности

49. Найдите число корней уравнения
Решение
Рассмотрим функцию
Область ее определения – вся прямая. Для отыскания
критических точек найдем производную:
Нули производной функции: и
-1 2
Значит на промежутке уравнение имеет 1 корень

50. В шар радиусом вписать цилиндр с радиусом основания и
высотой наибольшего объема.
Решение
По чертежу видно, что выполняется
равенство
Очевидно, что высота цилиндра будет
переменной, тогда
Высота принимает значение от 0 до ,
причем на концах отрезка объем равен нулю. Найдем
критические точки:
При этом значение объем будет максимальным:
Ответ:

51. № 1. Число 18 разбить на такие два слагаемые, чтобы
сумма квадратов была наименьшей.
Подсказка Решение
№ 2. Имеет ли уравнение корни на
промежутке [2;3]
Подсказка Решение

54. 1. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.
Алгебра и начала анализа: учеб. для 10-11 кл. – М.:
Просвещение, 2007.
2. Бевз Г.П. Алгебра и начала анализа6 учеб. для 11
кл.: академ. уровень, профил. уровень. – К.: Освіта,
2011.
3. Н.И. Шкиль, З.И. Слепкань, Е.С. Дубинчук. Алгебра
и начала анализа:учебник для 11 кл. - К.: Зодиак-
ЭКО, 2004.
4. А.Н. Колмогоров, А.М.Абрамова, Ю.П.Дудницын.
Алгебра и начала анализов: Учеб. Для 10-11 кл. –
М.: Просвещение, 1990