The document describes m-way search trees, B-trees, heaps, and their related operations. An m-way search tree is a tree where each node has at most m child nodes and keys are arranged in ascending order. B-trees are similar but ensure the number of child nodes falls in a range and all leaf nodes are at the same depth. Common operations like searching, insertion, and deletion are explained for each with examples. Heaps store data in a complete binary tree structure where a node's value is greater than its children's values.

1. Data Structure and
Algorithm (CS 102)
Ashok K Turuk
1

2. m-Way Search Tree
An m-way search tree T may be an empty
tree. If T is non-empty, it satisfies the
following properties:
(i) For some integer m known as the order
of the tree, each node has at most m
child nodes. A node may be represented
as A0 , (K1, A1), (K2, A2) …. (Km-1 ,
Am-1 ) where Ki 1<= i <= m-1 are the
keys and Ai, 0<=i<=m-1 are the
pointers to the subtree of T
2

3. m-Way Search Tree
[2] If the node has k child nodes where
k<=m, then the node can have only (k-1)
keys, K1 , K2 , …… Kk-1 contained in the
node such that Ki < Ki+1 and each of the
keys partitions all the keys in the subtrees
into k subsets
[3] For a node A0 , (K1 , A1), (K2 , A2) , ….
(Km-1 , Am-1 ) all key values in the subtree
pointed to by Ai are less than the key Ki+1
, 0<=i<=m-2 and all key values in the
subtree pointed to by Am-1 are greater
than Km-1
3

4. m-Way Search Tree
[4] Each of the subtree Ai , 0<=i<=m-1
are also m-way search tree
4

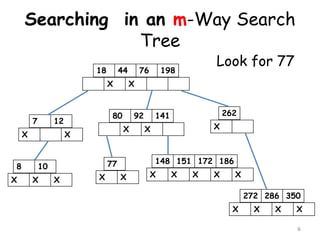
5. m-Way Search Tree [ m=5]
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
272 286 350
X X X X
5

6. Searching in an m-Way Search
Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
272 286 350
X X X X
Look for 77
6

7. Insertion in an m-Way Search
Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
272 286 350
X X X X
Insert 6
7

8. Insertion in an m-Way Search
Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X
X X X
77
X X
272 286 350
X X X X
Insert 6
6
X
Insert 146
146
X
8

9. Deletion in an m-Way Search
Tree
Let K be the key to be deleted from the
m-way search tree.
K
Ai Aj
K : Key
Ai , Aj : Pointers to subtree
9

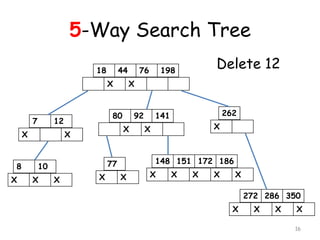
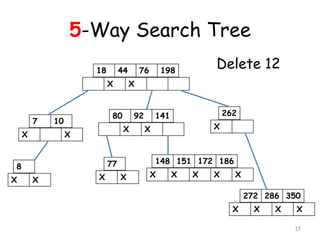
10. Deletion in an m-Way Search
Tree
[1] If (Ai = Aj = NULL) then delete K
[2] If (Ai  NULL, Aj = NULL ) then
choose the largest of the key elements
K’ in the child node pointed to by Ai and
replace K by K’.
[3] If (Ai = NULL, Aj  NULL ) then
choose the smallest of the key element
K” from the subtree pointed to by Aj ,
delete K” and replace K by K”.
10

11. Deletion in an m-Way Search
Tree
[4] If (Ai  NULL, Aj  NULL ) then
choose the largest of the key elements
K’ in the subtree pointed to by Ai or
the smallest of the key element K”
from the subtree pointed to by Aj to
replace K.
11

12. 5-Way Search Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
272 286 350
X X X X
Delete 151
12

13. 5-Way Search Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 172 186
X X X
X X X X
X X X
77
X X
272 286 350
X X X X
Delete 151
13

14. 5-Way Search Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
272 286 350
X X X X
Delete 262
14

15. 5-Way Search Tree
18 44 76 198
X X
7 12
X X
80 92 141 272
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
286 350
X X X
Delete 262
15

16. 5-Way Search Tree
18 44 76 198
X X
7 12
X X
80 92 141 262
8 10
148 151 172 186
X X X
X X X X X
X X X
77
X X
272 286 350
X X X X
Delete 12
16

17. 5-Way Search Tree
18 44 76 198
X X
7 10
X X
80 92 141 262
8
148 151 172 186
X X X
X X X X X
X X
77
X X
272 286 350
X X X X
Delete 12
17

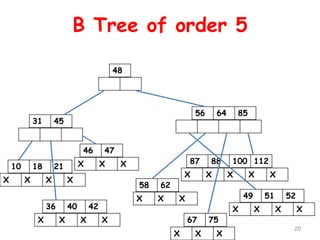
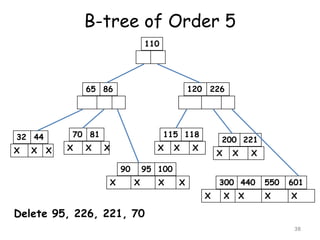
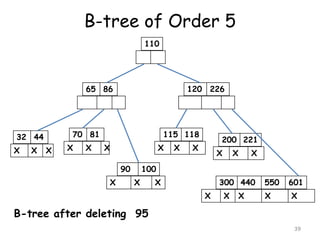
18. B Trees
B tree is a balanced m-way search tree
A B tree of order m, if non empty is an m-
way search tree in which
[i] the root has at least two child nodes and
at most m child nodes
[ii] internal nodes except the root have at
least m/2 child nodes and at most m
child nodes
18

19. B Trees
[iii] the number of keys in each internal
node is one less than the number of
child nodes and these keys partition the
keys in the subtrees of nodes in a
manner similar to that of m-way search
trees
[iv] all leaf nodes are on the same level
19

20. B Tree of order 5
48
31 45
56 64 85
87 88 100 112
X X X X X
49 51 52
X X X X
20
46 47
36 40 42
10 18 21
X X X X
X X X
X X X X
X X X
58 62
67 75
X X X

21. Searching a B Tree
Searching for a key in a B-tree is similar
to the one on an m-way search tree.
The number of accesses depends on the
height h of the B-tree
21

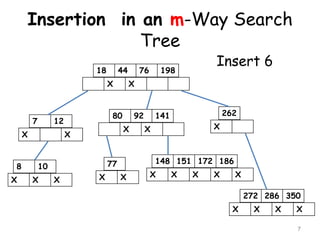
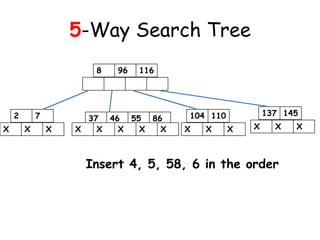
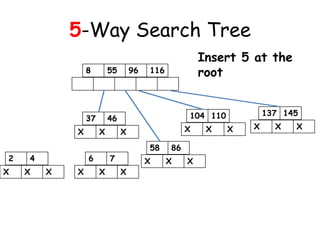
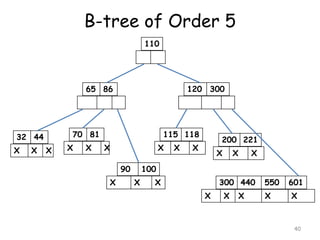
22. Insertion in a B-Tree
A key is inserted according to the
following procedure
[1] If the leaf node in which the key is to
be inserted is not full, then the
insertion is done in the node.
A node is said to be full if it contains a
maximum of (m-1) keys given the
order of the B-tree to be m
22

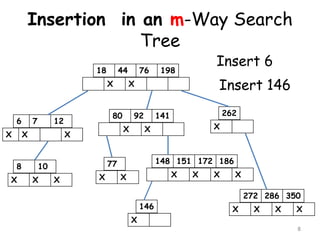
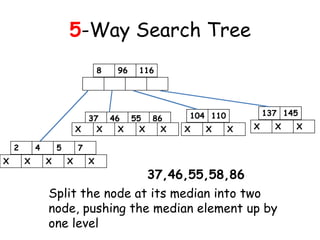
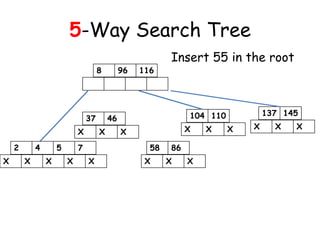
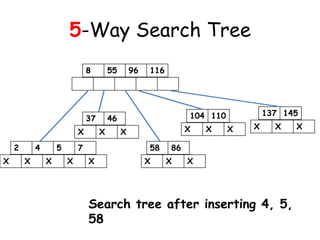
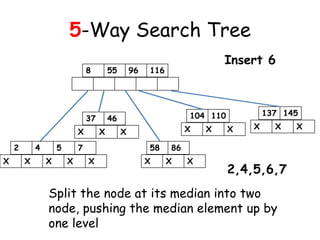
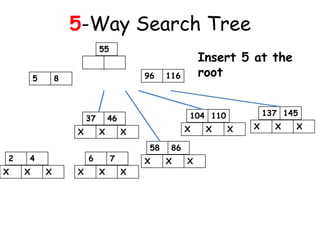
23. Insertion in a B-Tree
[2] If the node were to be full then insert
the key in order into the existing set of
keys in the node. Split the node at its
median into two nodes at the same level,
pushing the median element up by one level.
Accommodate the median element in the
parent node if it is not full. Otherwise
repeat the same procedure and this may
call for rearrangement of the keys in the
root node or the formation of new root
itself.
23

24. 5-Way Search Tree
8 96 116
2 7
X X X
104 11037 46 55 86
X X X X X X X X
137 145
X X X
Insert 4, 5, 58, 6 in the order

25. 5-Way Search Tree
8 96 116
104 11037 46 55 86
X X X X X X X X
137 145
X X X
Search tree after inserting 4
2 4 7
X X X X

26. 5-Way Search Tree
8 96 116
104 11037 46 55 86
X X X X X X X X
137 145
X X X
Search tree after inserting 4, 5
2 4 5 7
X X X X X

27. 5-Way Search Tree
8 96 116
104 11037 46 55 86
X X X X X X X X
137 145
X X X
2 4 5 7
X X X X X
37,46,55,58,86
Split the node at its median into two
node, pushing the median element up by
one level

28. 5-Way Search Tree
104 110
X X X
137 145
X X X
2 4 5 7
X X X X X
37 46
X X X
58 86
X X X
8 96 116
Insert 55 in the root

29. 5-Way Search Tree
104 110
8 55 96 116
X X X
137 145
X X X
Search tree after inserting 4, 5,
58
2 4 5 7
X X X X X
37 46
X X X
58 86
X X X

30. 5-Way Search Tree
104 110
8 55 96 116
X X X
137 145
X X X
Insert 6
2 4 5 7
X X X X X
37 46
X X X
58 86
X X X
2,4,5,6,7
Split the node at its median into two
node, pushing the median element up by
one level

31. 5-Way Search Tree
104 110
8 55 96 116
X X X
137 145
X X X
Insert 5 at the
root
37 46
X X X
58 86
X X X6 72 4
X X XX X X

32. 5-Way Search Tree
104 110
X X X
137 145
X X X
Insert 5 at the
root
37 46
X X X
58 86
X X X6 72 4
X X XX X X
96 1165 8
55

33. 5-Way Search Tree
104 110
X X X
137 145
X X X
Insert 5 at the
root
37 46
X X X
58 86
X X X
6 7
2 4
X X X
X X X
96 116
5 8
55

34. Deletion in a B-Tree
It is desirable that a key in leaf node be
removed.
When a key in an internal node to be
deleted, then we promote a successor or
a predecessor of the key to be deleted
,to occupy the position of the deleted
key and such a key is bound to occur in a
leaf node.
34

35. Deletion in a B-Tree
Removing a key from leaf node:
If the node contain more than the
minimum number of elements, then the
key can be easily removed.
If the leaf node contain just the minimum
number of elements, then look for an
element either from the left sibling
node or right sibling node to fill the
vacancy.
35

36. Deletion in a B-Tree
If the left sibling has more than minimum
number of keys, pull the largest key up
into the parent node and move down the
intervening entry from the parent node
to the leaf node where key is deleted.
Otherwise, pull the smallest key of the
right sibling node to the parent node
and move down the intervening parent
element to the leaf node.
36

37. Deletion in a B-Tree
If both the sibling node has minimum number
of entries, then create a new leaf node out
of the two leaf nodes and the intervening
element of the parent node, ensuring the
total number does not exceed the
maximum limit for a node.
If while borrowing the intervening element
from the parent node, it leaves the number
of keys in the parent node to be below the
minimum number, then we propagate the
process upwards ultimately resulting in a
reduction of the height of B-tree
37

38. B-tree of Order 5
38
110
65 86 120 226
70 8132 44
X X X
90 95 100
X X XX X X
115 118
200 221
X X X
X X X X 300 440 550 601
X X X X X
Delete 95, 226, 221, 70

39. B-tree of Order 5
39
110
65 86 120 226
70 8132 44
X X X
90 100
X X XX X X
115 118
200 221
X X X
X X X 300 440 550 601
X X X X X
B-tree after deleting 95

40. B-tree of Order 5
40
110
65 86 120 300
70 8132 44
X X X
90 100
X X XX X X
115 118
200 221
X X X
X X X 300 440 550 601
X X X X X

41. B-tree of Order 5
41
110
65 86 120 300
70 8132 44
X X X
90 100
X X XX X X
115 118
200 221
X X X
X X X 440 550 601
X X X X
B-tree after deleting 95, 226
Delete 221

42. B-tree of Order 5
42
110
65 86 120 440
70 8132 44
X X X
90 100
X X XX X X
115 118
200 300
X X X
X X X 550 601
X X X
B-tree after deleting 95, 226, 221
Delete 70

43. B-tree of Order 5
43
110
65 86 120 440
65 8132 44
X X X
90 100
X XX X X
115 118
200 300
X X X
X X X 550 601
X X X
Delete 65

44. B-tree of Order 5
44
11086 120 440
65 8132 44
X X X
90 100
X XX X X
115 118
200 300
X X X
X X X 550 601
X X X
B-tree after deleting 95, 226, 221, 70

45. Heap
Suppose H is a complete binary tree with
n elements
H is called a heap or maxheap if each
node N of H has the following property
Value at N is greater than or equal to the
value at each of the children of N.
45

46. Heap
46
97
88 95
66 55
66 35
18 40 30 26
48
24
55
95
62 77
48
25 38
9
7
8
8
9
5
6
6
5
5
9
5
4
8
6
6
3
5
4
8
5
5
6
2
7
7
2
5
3
8
1
8
4
0
3
0
2
6
2
4
1 2 3 4 5 6 7 8 9 1
0
11 1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0

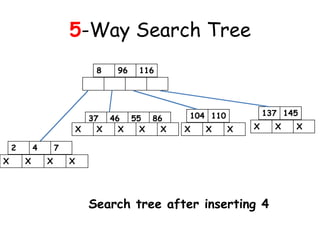
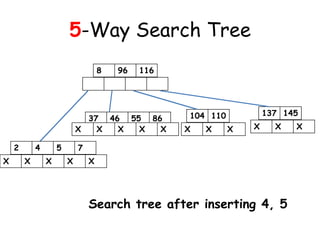
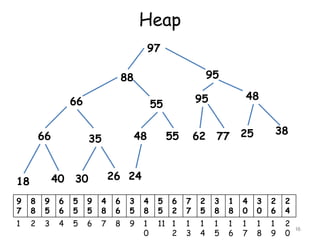
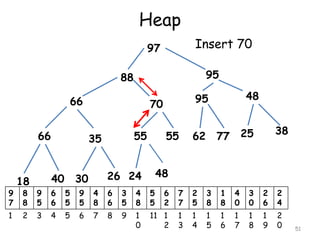
47. Inserting into a Heap
Suppose H is a heap with N elements
Suppose an ITEM of information is given.
Insertion of ITEM into heap H is given as follows:
[1] First adjoin ITEM at the end of H so that H is
still a complete tree, but necessarily a heap
[2] Let ITEM rise to its appropriate place in H so
that H is finally a heap
47

48. Heap
48
97
88 95
66 55
66 35
18 40 30 26
48
24
55
95
62 77
48
25 38
9
7
8
8
9
5
6
6
5
5
9
5
4
8
6
6
3
5
4
8
5
5
6
2
7
7
2
5
3
8
1
8
4
0
3
0
2
6
2
4
1 2 3 4 5 6 7 8 9 1
0
11 1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
Insert 70
70

49. Heap
49
97
88 95
66 55
66 35
18 40 30 26
48
24
55
95
62 77
48
25 38
9
7
8
8
9
5
6
6
5
5
9
5
4
8
6
6
3
5
4
8
5
5
6
2
7
7
2
5
3
8
1
8
4
0
3
0
2
6
2
4
1 2 3 4 5 6 7 8 9 1
0
11 1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
Insert 70
70

50. Heap
50
97
88 95
66 55
66 35
18 40 30 26
70
24
55
95
62 77
48
25 38
9
7
8
8
9
5
6
6
5
5
9
5
4
8
6
6
3
5
4
8
5
5
6
2
7
7
2
5
3
8
1
8
4
0
3
0
2
6
2
4
1 2 3 4 5 6 7 8 9 1
0
11 1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
Insert 70
48

51. Heap
51
97
88 95
66 70
66 35
18 40 30 26
55
24
55
95
62 77
48
25 38
9
7
8
8
9
5
6
6
5
5
9
5
4
8
6
6
3
5
4
8
5
5
6
2
7
7
2
5
3
8
1
8
4
0
3
0
2
6
2
4
1 2 3 4 5 6 7 8 9 1
0
11 1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
Insert 70
48

52. Build a Heap
Build a heap from the following list
44, 30, 50, 22, 60, 55, 77, 55
52

53. 53
44
44, 30, 50, 22, 60, 55, 77, 55
44
30
44
30 50
50
30 44
50
30 44
22
Complete the Rest Insertion
77
55 60
50 30
22
44 55

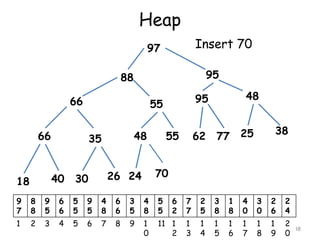
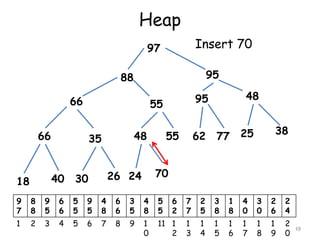
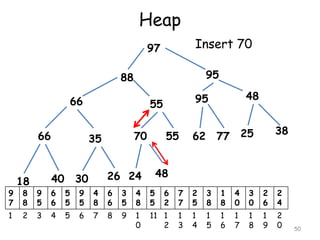
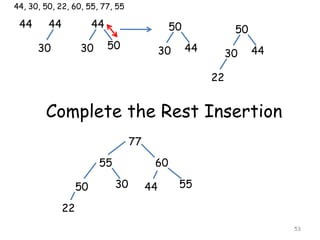
54. Deleting the Root of a Heap
Suppose H is a heap with N elements
Suppose we want to delete the root R of H
Deletion of root is accomplished as follows
[1] Assign the root R to some variable ITEM
[2] Replace the deleted node R by the last
node L of H so that H is still a complete
tree but necessarily a heap
[3] Reheap. Let L sink to its appropriate
place in H so that H is finally a heap.
54

55. 55
95
85 70
55 33
15
30 65
20 15 22
22
85 70
55 33
15
30 65
20 15
85
22 70
55 33
15
30 65
20 15
85
55 70
22 33
15
30 65
20 15