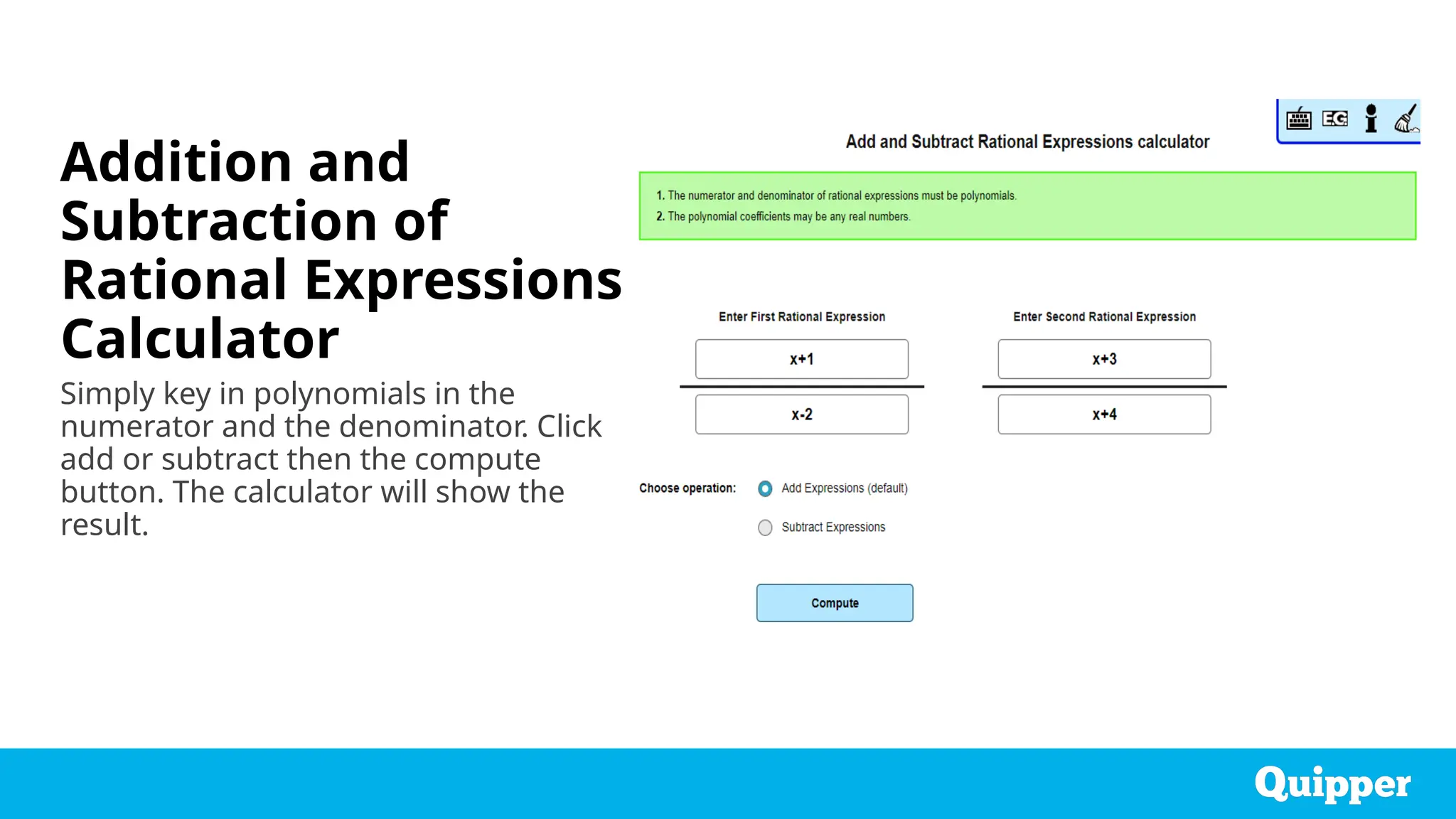
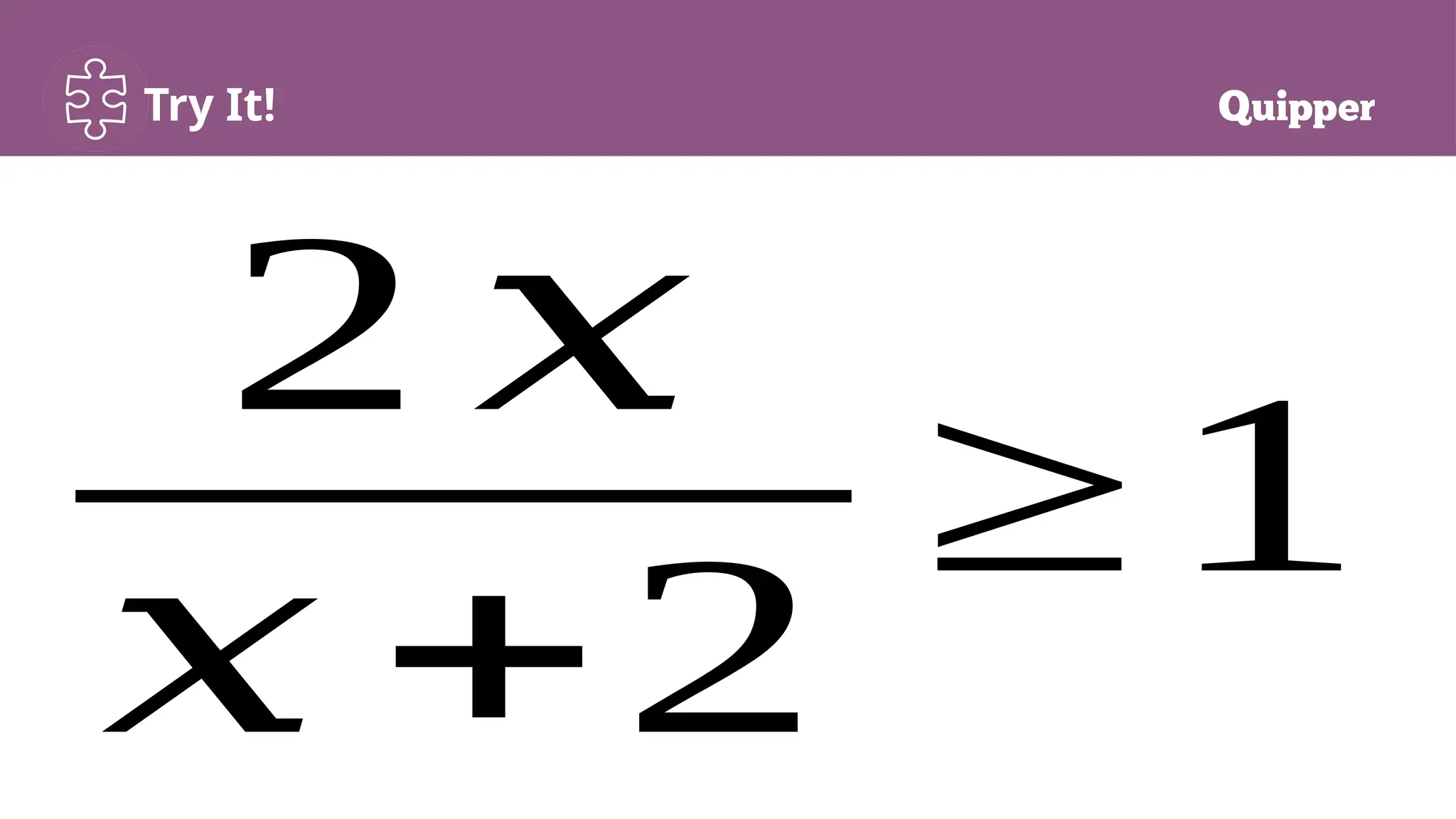This lesson focuses on defining and solving rational inequalities, emphasizing the importance of understanding critical values and the steps involved in solving them. Key methodologies include the use of number lines to identify solution intervals and constructing tables of signs to determine where the rational expression is positive or negative. Students will engage in both individual and group practice to reinforce their understanding and application of rational inequalities.

1. Lesson 3
Rational Inequalities

2. Objectives
At the end of this lesson, the learner should be able to
● correctly define rational inequalities and critical
values; and
● accurately solve rational inequalities.

3. Essential Questions
● What are critical values?
● What are rational inequalities?
● How do you solve rational inequalities?

4. Warm Up!
The skill of adding and subtracting rational expressions is
important as we learn how to solve rational inequalities. let
us first recall how to add or subtract rational expressions
using this online calculator which can be found using the link
below:
https://www.mathportal.org/calculators/rational-
expressions/add-subtract-rational-calculator.php

5. Addition and
Subtraction of
Rational Expressions
Calculator
Simply key in polynomials in the
numerator and the denominator. Click
add or subtract then the compute
button. The calculator will show the
result.

6. Guide Questions
● What are rational expressions?
● How do we add or subtract rational expressions?

7. Learn about It!
1 Inequality
shows a comparison between different quantities or expressions using the
symbols , , , , or
Example:
The expression shows a comparison between and .

8. Learn about It!
2
Rational Inequality
uses any of the symbols , , , , or , and contains at least one rational expression
Example:
The expressions is a rational inequality.

9. Learn about It!
3 Critical Value (of a rational expression)
a number that makes the expression undefined or equal to zero.
Example:
In the expression , the critical values are and -1 because 2
make makes it zero and -1 makes it undefined.

10. Try It!
Example 1: Solve the rational inequality .
Solution:
1. Rewrite the inequality such that the left-hand side is
written as a single rational expression and the right-hand
side becomes zero.

11. Try It!
2 𝑥
𝑥 +2
≥1

12. Try It!
2. Factor the numerator and the denominator.
Both the numerators and denominators are completely
factored.
3. Find the critical values of the rational expression on the
left-hand side of the inequality. This can be done by writing
the numerator and the denominator separately, equating
each of them to zero, and solving the resulting equations.

13. Try It!
Numerator:
Denominator:
The critical values are and .

14. Try It!
The roots of the numerator make the rational
expression equal to 0. Thus, these values must be included
in the final solution set. The root of the denominator,
however, is not included because it will make the rational
expression undefined.
4. Use the critical values as bounds to divide the set of real
numbers into intervals. Remember the following guidelines:
a. The symbols and always come with parentheses
because they cannot possibly be included in any interval
of real numbers.

15. Try It!
b. If the inequality involves the strict inequality
symbols , , or , all intervals should be enclosed in
parentheses because their endpoints cannot possibly
become part of the solution set.
c. If the inequality involves the non-strict inequality
symbols or , the roots of the numerator should be
included in their respective intervals using the symbols
or , while the roots of the denominator should be
excluded using the symbols or .

16. Try It!
The number line helps you to divide the set of real
numbers into intervals. Use a shaded circle if the value is
included in the solution set, and a hollow circle if not. (The
number line below is not drawn to scale.)
As indicated by the previous guidelines, we use the
critical values and to divide the set of real numbers into the
intervals , , .

17. Try It!
5. Construct a table of signs for the rational inequality. The
top row of the table should contain the intervals from the
previous step, while the leftmost column should contain the
test point, the factors of the numerator, and the factors of
the denominator. Add another row at the bottom for the
entries that correspond to the entire rational expression.

18. Try It!
Test Point

19. Try It!
6. To fill an entry on the table, choose a convenient number
from the corresponding interval on top (do not choose a
critical value). Substitute this number into the expression on
the left, then simplify. Take the sign of the answer you
obtained (the actual value does not matter) and write it on
the table.

20. Try It!
Test Point

21. Try It!
7. Determine the sign of the entire rational expression for
each interval by multiplying the signs in each column. Write
the answers in the last row of the table.
Test Point

22. Try It!
8. Determine the solution set by forming the union of all
intervals that satisfy the inequality.
Recall that the left-hand side of the inequality is the rational
expression in the bottom row of the table, and this inequality
states that the rational expression is greater than or equal to
zero. This means that our solution set consists of intervals for
which the expression is positive. These intervals are and as
shown in the table.
Therefore, the solution of the inequality is .

23. Try It!
Another method may be used in solving rational
inequalities. We call this as the method of test values. The
steps 1-4 of the abovementioned method are just the same. The
next steps are as follows:
5. Choose a convenient test value for each interval.
Substitute each of the chosen values to the given rational
inequality and simplify.

24. Try It!
Test Point: Test Point: Test Point:
The statement is true.
Thus, the interval is a
solution.
The statement is
false. Thus, the
interval is not a
solution.
The statement is true.
Thus, the interval is a
solution.

25. Try It!
6. Determine the solution set by forming the union of all
intervals that satisfy the inequality.
Therefore, the solution set of the inequality is .

26. Try It!
Note:
Unlike in solving rational equations, it is not valid to multiply
both sides of an inequality by a variable. Multiplying both sides
of an inequality by a positive number retains the inequality
symbol, while multiplying both sides of an inequality by a
negative number reverses the inequality symbol. The sign of the
variable is unknown. Thus, it is not valid to multiply both sides
of an inequality by a variable.

27. Try It!
Example 2: Solve for in the rational inequality .
Solution:
1. Rewrite the inequality such that the left-hand side is
written as a single rational expression and the right-hand
side becomes zero.
In this case, we do not have to manipulate the
inequality because the left-hand side is written as a single
expression, while the right-hand side is already zero.

28. Try It!
2. Factor the numerator and the denominator.
3. Find the critical values of the rational expression on the
left-hand side of the inequality. This can be done by writing
the numerator and the denominator separately, equating
each of them to zero, and solving the resulting equations.

29. Try It!
Numerator:
Denominator:

30. Try It!
The critical values are and .
4. Use the critical values as bounds to divide the set of real
numbers into intervals.
The values and are not included in the solution set
since they make the fraction equal to zero. The value is also
not included in the solution set since it makes the fraction
undefined.

31. Try It!
We use the critical values and to divide the set of real
numbers into the intervals, , , , and .
5. Construct a table of signs for the rational inequality.

32. Try It!
Test Point

33. Try It!
6. Fill out the entries of the table.
Choose a convenient number from the corresponding
interval on top (do not choose a critical value). Substitute
this number into the expression on the left, then simplify.
Take the sign of the answer you obtained (the actual value
does not matter), and write it on the table.

34. Try It!
Test Point

35. Try It!
7. Determine the sign of the entire rational expression for
each interval by multiplying the signs in each column. Write
the answers in the last row of the table.
Test Point

36. Try It!
8. Determine the solution set by forming the union of all
intervals that satisfy the inequality.
The rational expression in the left-hand side of the
inequality is less than zero. This means that our solution set
consists of intervals for which the expression is negative. These
intervals are and as shown in the table.
Therefore, the solution of the inequality is .

37. Let’s Practice!
Individual Practice:
1. Solve the rational inequality .
2. Solve for in the rational inequality .

38. Let’s Practice!
Group Practice: To be done in groups of three
1. Solve: .
2. A drug is injected into the bloodstream of a patient
through his arm. The concentration (in milligrams per
liter) of the drug in the bloodstream hours after the
injection is approximately given by . When will the
concentration of the drug in the arm be 0.02 milligram
per milliliter or greater?

39. Key Points
1 Inequality
shows a comparison between different quantities or expressions using the
symbols , , , , or .
2
Rational Inequality
uses any of the symbols , , , , or whose terms are rational expressions.
.
3
Critical Value (of a rational expression)
a number that makes the expressions undefined or equal to zero.

40. Synthesis
● How do you solve rational inequalities?
● Why are rational inequalities important in our lives?
● In what areas can we apply rational inequalities?