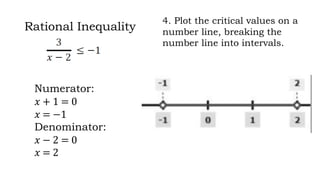
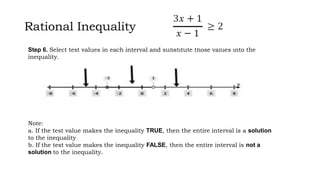
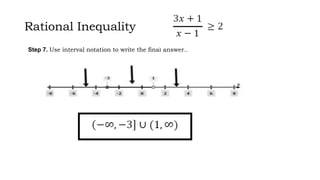
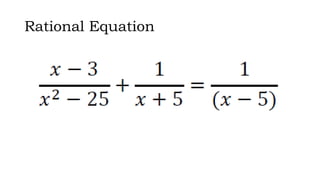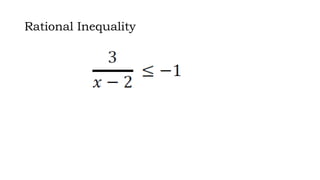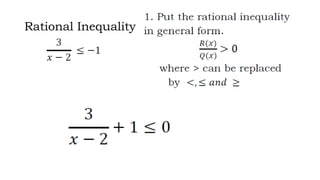This document discusses how to solve rational equations and inequalities. It provides steps for solving rational equations, which include finding the least common denominator, multiplying both sides by the LCD, applying the distributive property, and checking solutions. It also outlines six steps for solving rational inequalities: writing the inequality as a single rational expression, setting the numerator and denominator equal to zero to find critical values, plotting critical values on a number line, substituting critical values into the inequality, selecting test values in each interval, and using interval notation to write the final answer.

1. Solving Rational
Equations and
Inequalities
M11GM-Ib-3
solves rational equations and inequalities.

2. Rational Equation

3. 1. Find the Least Common Denominator(LCD).

4. 2. Multiply both sides of the equation by it’s the LCD.

5. 3. Apply the Distributive Property and then simplify.

6. 4. Find all the possible values of x.

7. 5. Check each value by substituting into original equation
and reject any extraneous root/s

8. Rational Inequality

9. Rational Inequality

10. Rational Inequality

11. Rational Inequality

12. Rational Inequality
2. Write the inequality into a single
rational expression on the left side.
(You can refer to the review section
for solving unlike denominators)

13. Rational Inequality
4. Plot the critical values on a
number line, breaking the
number line into intervals.
Numerator:
𝑥 + 1 = 0
𝑥 = −1
Denominator:
𝑥 − 2 = 0
𝑥 = 2

14. Rational Inequality
5. Substitute critical values to the inequality to
determine if the endpoints of the intervals in the
solution should be included or not.
Numerator:
𝑥 + 1 = 0
𝑥 = −1
Denominator:
𝑥 − 2 = 0
𝑥 = 2

15. Rational Inequality
5. Select test values in each interval and substitute
those values into the inequality.
Note:
If the test value makes the inequality true, then the
entire interval is a solution to the inequality.
If the test value makes the inequality false, then the
entire interval is not a solution to the inequality.

16. Rational Inequality
6. Use interval notation or set notation to write the
final answer.

17. Rational Inequality
Step 1. Put the rational inequality in the general form where > can be replaced by
<, ≤ 𝑎𝑛𝑑 ≥.
Step 2. Write the inequality into a single rational expression on the left-hand side.
Step 3. Set the numerator and denominator equal to zero and solve. The values you
get are called critical values.
Step 4. Plot the critical values on a number line, breaking the number line into
intervals.
Step 5. Substitute critical values to the inequality to determine if the endpoints of
the intervals in the solution should be included or not.

18. Rational Inequality
Step 6. Select test values in each interval and substitute those values into the
inequality.
Note:
a. If the test value makes the inequality TRUE, then the entire interval is a solution
to the inequality
b. If the test value makes the inequality FALSE, then the entire interval is not a
solution to the inequality.

19. Rational Inequality
Step 7. Use interval notation to write the final answer..