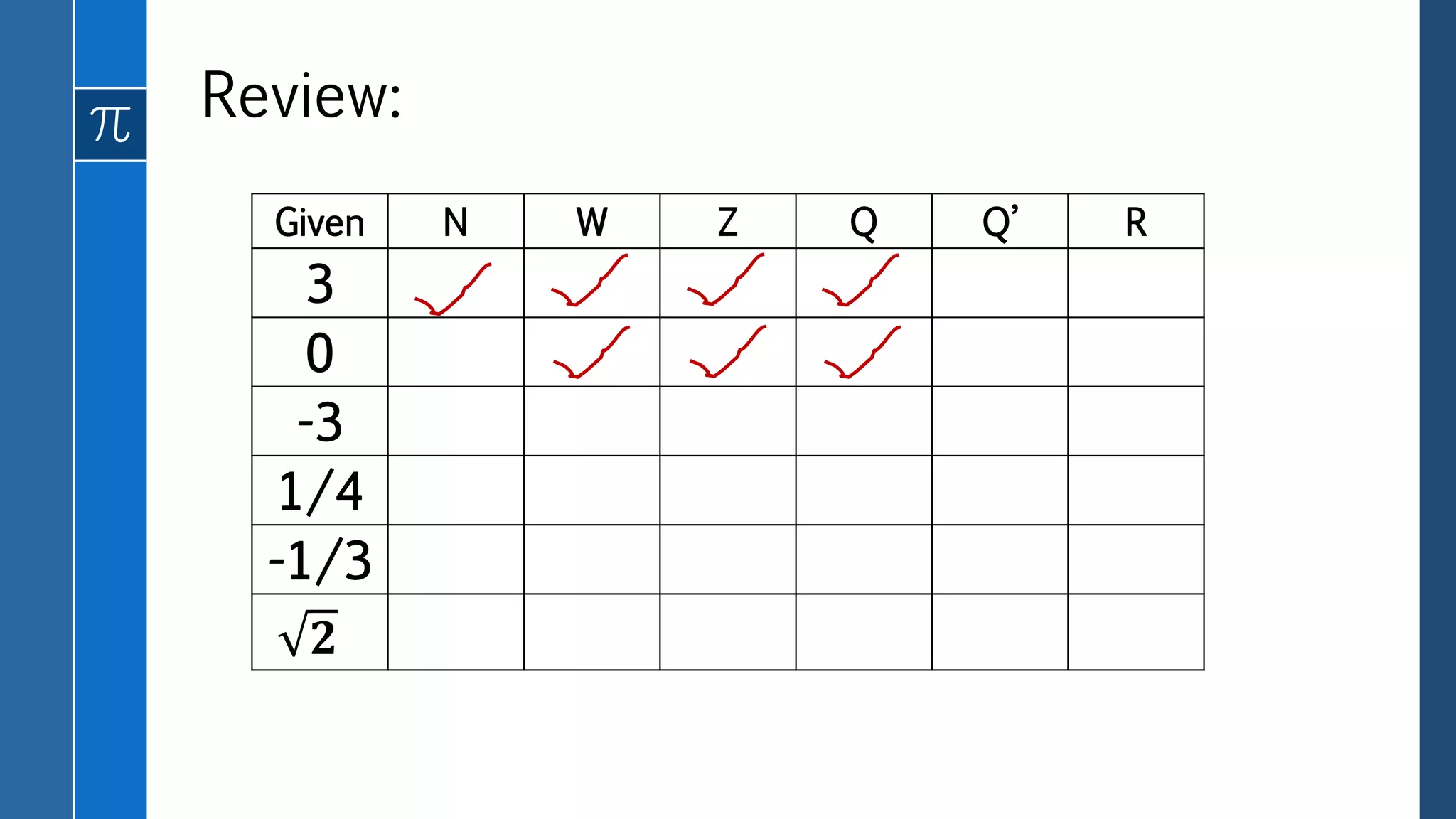
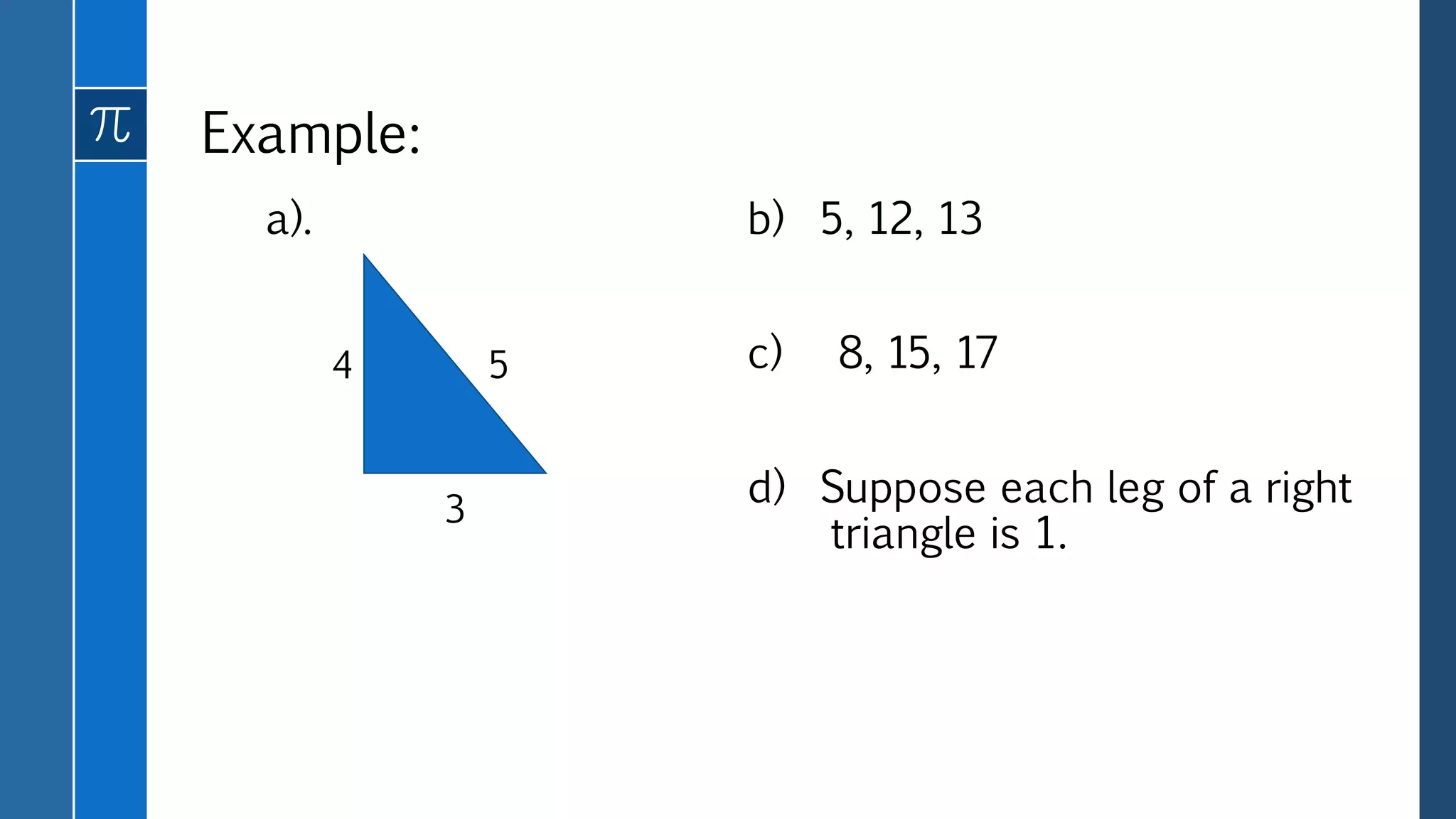
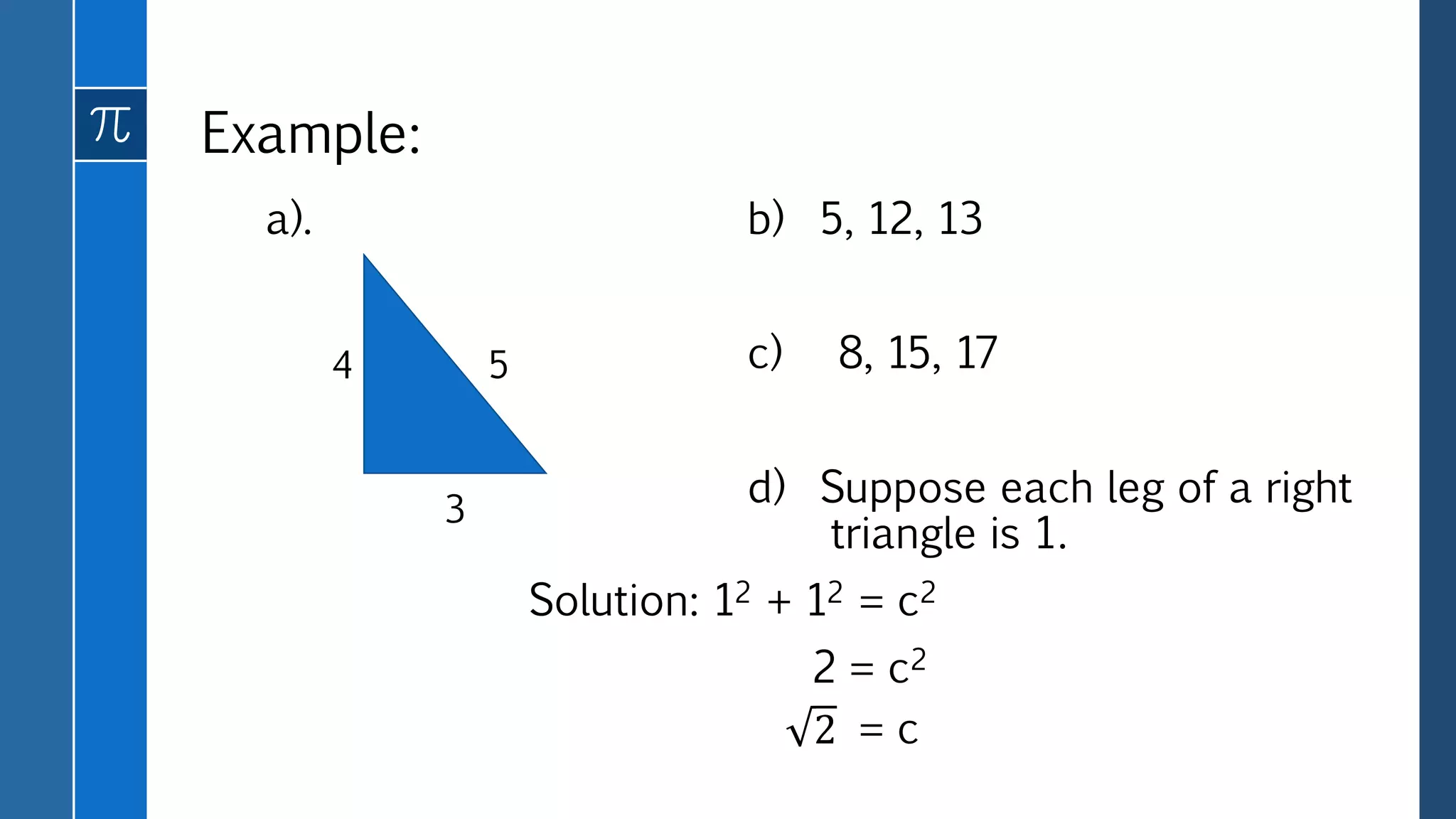
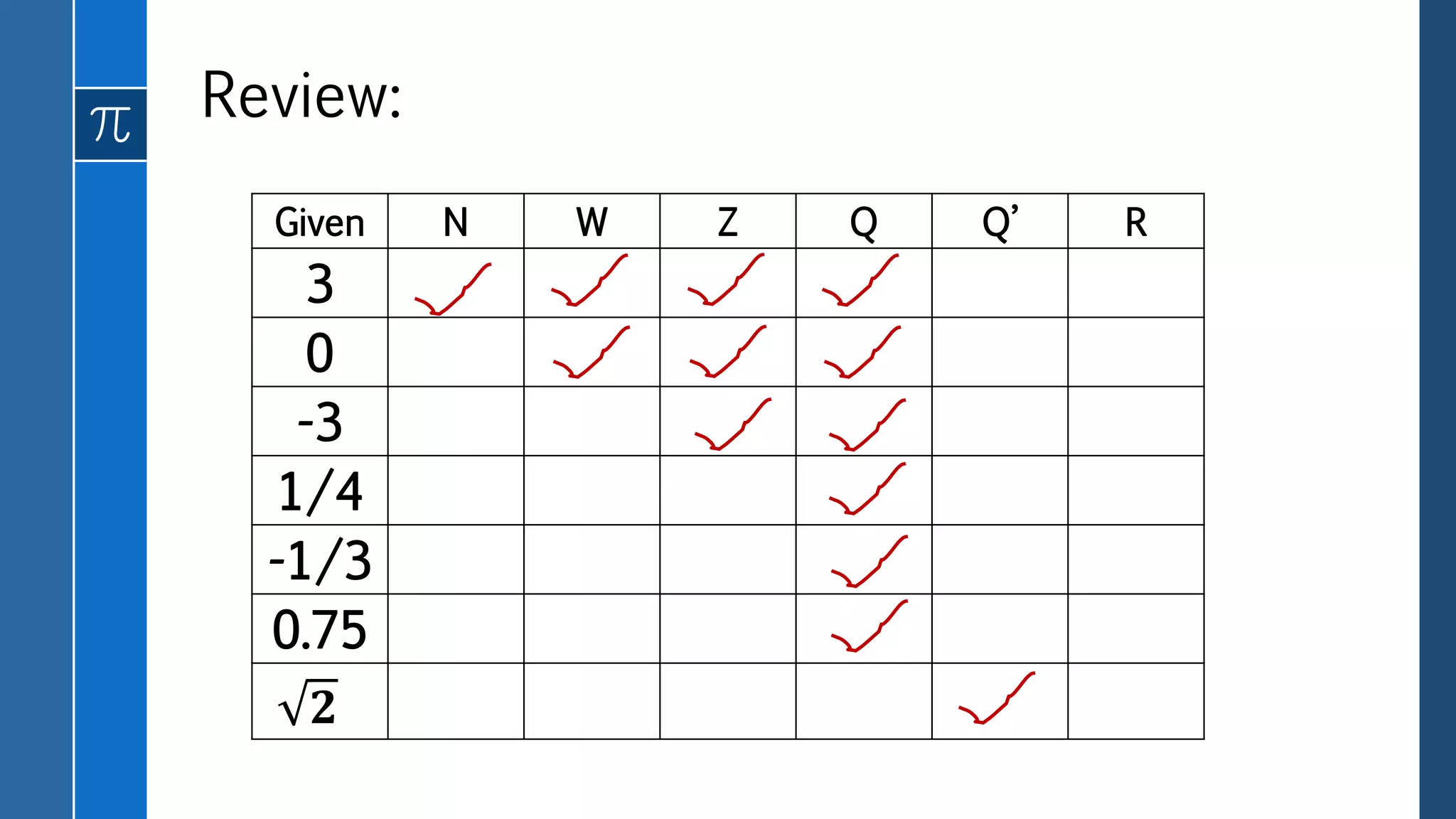
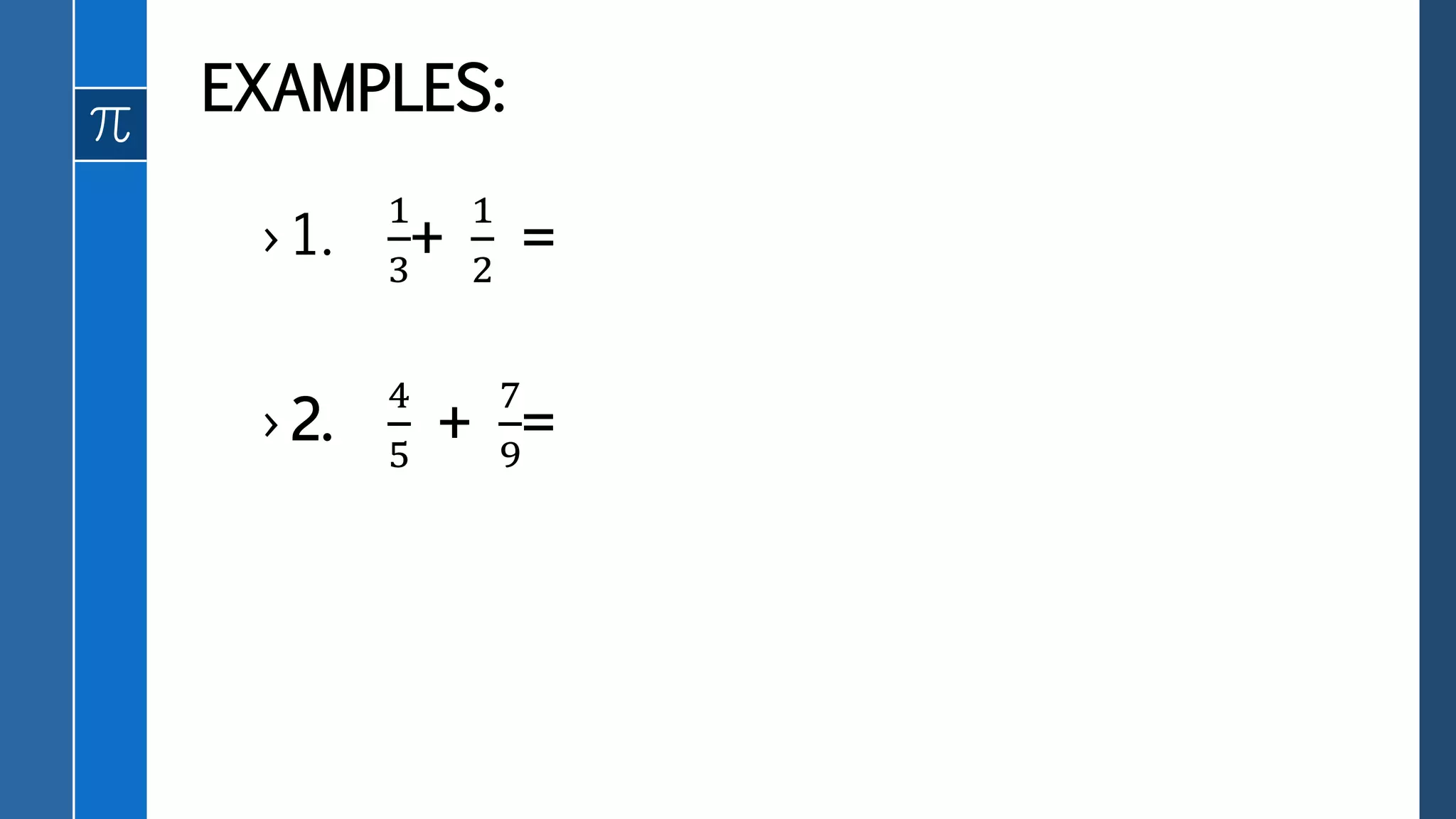This document defines and provides examples of different types of real numbers including rational and irrational numbers. It discusses how rational numbers can be represented as fractions or decimals, and how to convert between fraction and decimal representations. Irrational numbers are defined as having non-terminating, non-repeating decimal representations. The key types of real numbers - natural numbers, integers, rational numbers, and irrational numbers - are related in a Venn diagram with their union being the set of all real numbers.

1. Real Numbers
www.slideshare.net/reycastro1
The Nature of Modern Mathematics

2. Introduction:
RATIONALS
The society that we have been
considering has used numbers only as
they relate to practical problems.
However, this need not be the case,
since numbers can be appreciated for
their beauty and interrelationships.

3. DEFINITION:
The rational number
𝟒
𝟓
is interpreted as the
quotient obtained when 4 is divided by 5.
RATIONAL NUMBERS
The rational numbers, denoted by ℚ, are the set
of all numbers of the form
𝓹
𝓺
, where 𝓹 and 𝓺 are
integers and 𝓺 ≠ 𝟎.

4. Thus,
𝟓
𝟗
,
−𝟏𝟏
𝟏𝟑
,
𝟓
𝟏
,
𝟎
𝟏𝟕
,
−𝟏𝟎
𝟓
, and
𝟐𝟓
𝟓
are all elements of ℚ.
RATIONAL NUMBERS

5. Notice that,
𝟓
𝟏
,
𝟐𝟓
𝟓
,
−𝟏𝟎
−𝟐
, …
represent the same numbers.
𝒂
𝒃
=
𝒄
𝒅
means ad = bc.
RATIONAL NUMBERS

6. Thus we see that,
𝟐𝟓
𝟓
=
−𝟏𝟎
−𝟐
,
since
25(-2) = 5(-10)
-50 = -50
Also, 125/70 ≠ 73/41 why?
RATIONAL NUMBERS

7. If a/b and c/d are rational numbers, then
𝒂
𝒃
+
𝒄
𝒅
=
𝒂𝒅 + 𝒃𝒄
𝒃𝒅
.
where a, b, c, d are integers, b and d
nonzero.
ADDITION OF RATIONALS

8. › 1.
1
3
+
1
2
=
› 2.
4
5
+
7
9
=
EXAMPLES:

9. If a/b and c/d are rational numbers, then
𝒂
𝒃
−
𝒄
𝒅
=
𝒂𝒅 − 𝒃𝒄
𝒃𝒅
.
where a, b, c, d are integers, b and d
nonzero.
SUBTRACTION OF RATIONALS
Example: 1.
𝟐
𝟑
−
−𝟏
𝟐
= 2.
𝟒
𝟗
−
𝟕
𝟗
=

10. If a/b and c/d are rational numbers, then
𝒂
𝒃
∙
𝒄
𝒅
=
𝒂𝒄
𝒃𝒅
.
MULTIPLICATION OF RATIONALS
Example: 1.
𝟒
𝟓
∙
𝟕
𝟗
= 2.
−𝟑
𝟓
∙
−𝟏
𝟐
=

11. If a/b and c/d are rational numbers,
c≠ 0, then
𝒂
𝒃
𝒄
𝒅
=
𝒂𝒅
𝒃𝒄
.
DIVISION OF RATIONALS
Example: 1.
−𝟑
𝟒
÷
−𝟒
𝟕
= 2.
𝟒
𝟓
÷
𝟕
𝟗
=

12. A. 1. Find the sum.
a.
𝟐
𝟑
+
𝟕
𝟗
b.
−𝟓
𝟕
+
𝟒
𝟑
c.
−𝟏𝟐
𝟑𝟓
-
𝟖
𝟏𝟓
d.
𝟒
𝟓
+ 𝟐 +
−𝟕
𝟐𝟓
e. 2-1 + 2
PROBLEM SET:

13. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
𝟐
Review:

14. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
𝟐
Review:

15. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
𝟐
Review:

16. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
𝟐
Review:

17. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
𝟐
Review:

18. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
0.75
𝟐
Review:

19. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
0.75
𝟐
Review:

20. Pythagoreans discovered the famous
property of square numbers that today
bears Pythagoras’ name.
“In any right triangle, the area of the
larger square was equal to the sum of the
areas of the smaller squares.
a2 + b2 = c2
IRRATIONALS

21. Example:
a). b) 5, 12, 13
c) 8, 15, 17
d) Suppose each leg of a right
triangle is 1.
3
4 5

22. Example:
a). b) 5, 12, 13
c) 8, 15, 17
d) Suppose each leg of a right
triangle is 1.
Solution: 12 + 12 = c2
2 = c2
3
4 5
2 = c

23. Recall:
› An integer is even if it is a multiple of 2.
expressed as 2k, for any integer k.
› An integer that is not even is said to be odd.
expressed as 2k + 1, for any integer k.

24. Argument:
Is 2 a is a rational a/b, where a and b are
integers and b is not 0?

25. The necessity of still another set of numbers
› The set of Irrational Numbers; notation ( Q’ ).
2 is irrational
also be 3, 5 and 7
and the square root of any number that is not a
perfect square. and so on

26. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
0.75
𝟐
Review:

27. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
0.75
𝟐
Review:

28. Real Numbers
Definition: The set of real numbers, denoted
by R, is defined as the union of the set of
rationals and the set of irrationals.

29. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
0.75
𝟐
Review:

30. Given N W Z Q Q’ R
3
0
-3
1/4
-1/3
0.75
𝟐
Review:

31. Real numbers that are rational
› Real numbers that are rational can be terminating
decimal
example:
1
4
= 0.25 and
5
8
= 0.625
Can be represented by repeating decimals
example:
2
3
= 0.66 … and
5
11
= 0.4545 …

32. Real numbers that are irrational
› Real numbers that are irrational have decimal
representations are nonterminating and nonrepeating.
example: 2 = 1.414214 … and 𝜋 = 3.1415926 …

33. Real Numbers
› We can say that the real numbers may be classified in
several ways.
› Any real number is;
1. positive, negative, or zero.
2. a rational number or an irrational number.
3. expressible as terminating, a repeating, or a
nonterminating and non-repeating decimal:

34. A set of Real Numbers
RQ’Q
ZW
N
-Z0

35. Changing From one representation to another
› From fraction to decimal
Given a fraction a/b, we change it to a decimal; a/b
means a divided by b.
Example: 1. Change 4/5 to decimal ans. 0.8
2. Change 1/7 to a decimal ans. 0.142857…
3. Change 6
2
9
to a decimal ans. 6. 2

36. Changing From one representation to another
From decimal to fraction
A. If decimal is terminating
a) 0.123 means 0.123/1000
b) 6.28 means
c) 0.349 means

37. Changing From one representation to another
From decimal to fraction
B. If decimal is repeating
procedure:
1. Let n=repeating decimal
2. Multiply both sides of the equation by 10k where k is
the number of digits repeating.
3. Subtract the original equation.
4. Solve the resulting equation for n.

38. If decimal is repeating
› Example:
a) Change 0. 7 to fraction
b) Change 0. 123 to fraction
c) Change 7. 564 to fraction

39. Try it! Problem set
› 1. What is the distinguishing characteristic between the
rational and irrational numbers?
› 2. Draw a Venn Diagram showing the natural numbers,
integers, rationals, and irrationals where the universe is
the set of reals.
› 3.

40. THANK YOU
www.slideshare.net/reycastro1
@reylkastro2
reylkastro