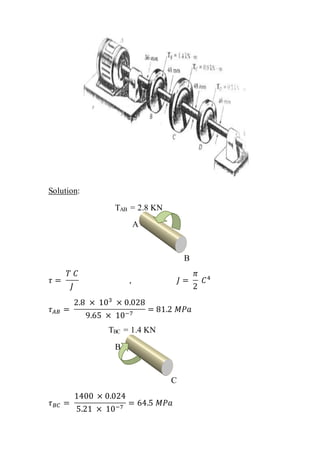
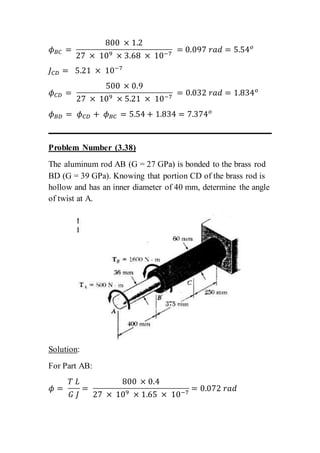
The document contains solutions to multiple problems involving determining shear stress, torque, and angle of twist in shaft and rod systems. Key details include formulas for calculating shear stress given torque and geometry, determining required diameters to not exceed allowable stress, and calculating angle of twist between sections using torque, length, shear modulus, and polar second moment of area. Examples analyze hollow and solid shafts made of materials like steel, brass, and aluminum under different torque conditions.

1. Problem Number (3.3)
Knowing that the internal diameter of the hollow shaft
shown is d = 22 mm, determine the maximum shearing stress
caused by a torque of magnitude T = 900N.m.
Solution:
𝜏 =
𝑇 𝐶
𝐽
, 𝐽 =
𝜋
2
𝐶4
𝜏 =
900 × 20 × 10−3
3.14
2
(0.024 − 0.0114)
= 78.87 𝑀𝑃𝑎
Problem Number (3.8)
The solid spindle AB has a diameter ds = 38 mm and is
made of a steel with an allowable shearing stress of 84 MPa,
while sleeve CD is made of a brass with an allowable shearing
stress of 50 MPa. Determine the largest torque T that can be
applied at A.

2. Solution:
𝜏 =
𝑇 𝐶
𝐽
, 𝐽 =
𝜋
2
𝐶4
𝑇 =
𝜏 𝐽
𝐶
, 𝐹𝑜𝑟 ℎ𝑜𝑙𝑙𝑜 𝐶𝑦𝑙𝑖𝑛𝑑𝑟𝑒: 𝐽 =
𝜋
2
( 𝐶 𝑜𝑢𝑡𝑒𝑟
4
− 𝐶𝑖𝑛𝑛𝑒𝑟
4
)
𝐹𝑜𝑟 𝑠𝑜𝑙𝑖𝑑 𝑠𝑝𝑖𝑛𝑑𝑙𝑒 𝐴𝐵:
𝑇 =
84 × 106
× 2.046 × 10−7
0.019
= 904.565 𝑁. 𝑚
𝐹𝑜𝑟 𝑠𝑙𝑒𝑒𝑣𝑒 𝐶𝐷:
𝑇 =
50 × 106
× 1.558 × 10−6
0.0375
= 2077.5 𝑁. 𝑚
Problem Number (3.11)
Under normal operating conditions, the electric motor
exerts a torque of 2.8 KN.m on shaft AB. Knowing that each
shaft is solid, determine the maximum shearing stress in (a)
shaft AB, (b) shaft BC, (c) shaft CD.

3. Solution:
TAB = 2.8 KN
A
B
𝜏 =
𝑇 𝐶
𝐽
, 𝐽 =
𝜋
2
𝐶4
𝜏 𝐴𝐵 =
2.8 × 103
× 0.028
9.65 × 10−7
= 81.2 𝑀𝑃𝑎
TBC = 1.4 KN
B
C
𝜏 𝐵𝐶 =
1400 × 0.024
5.21 × 10−7
= 64.5 𝑀𝑃𝑎

4. TCD = 0.5 KN
C
D
𝜏 𝐶𝐷 =
500 × 0.024
5.21 × 10−7
= 23.033 𝑀𝑃𝑎
Problem Number (3.17)
The solid shaft shown is formed of a brass for which the
allowable shearing stress is 55 MPa. Neglecting the effect of
stress concentrations, determine the smallest diameter dAB and
dBC for which the allowable shearing stress is not exceeded.
Solution:
TAB = 800N
A
B

5. 𝜏 =
𝑇 𝐶
𝐽
, 𝐽 =
𝜋
2
𝐶4
𝜏 𝐴𝐵 =
800 × 𝐶
3.14
2
𝐶4
= 55 × 106
∴ 𝐶 = 21 𝑚𝑚 , ∴ 𝑑 𝐴𝐵 = 42 𝑚𝑚
TBC = 400 N
B
C
𝜏 𝐵𝐶 =
400 × 𝐶
3.14
2
𝐶4
= 55 × 106
∴ 𝐶 = 16.67 𝑚𝑚 , ∴ 𝑑 𝐵𝐶 = 33.34 𝑚𝑚
Problem Number (3.20)
The solid rod BC has a diameter of 30 mm and is made of an
aluminum for which the allowable shearing stress is 25 MPa.
Rod AB is hollow and has an outer diameter of 25 mm; it is
made of a brass for which the allowable shearing stress is 50
MPa. Determine (a) the largest inner diameter of rod AB for
which the factor of safety is the same for each rod.(b) the largest
torque that can be applied at A.

6. Solution:
𝑇 =
𝜏 𝐽
𝐶
=
25 × 106
× 7.948 × 10−8
15 × 10−3
= 132.5 𝑁. 𝑚
𝐽 =
𝑇 𝐶
𝜏
=
132.5 × 12.5 × 10−3
50 × 106
=
3.14
2
(2.44 × 10−8
− 𝐶4
)
𝐶 = 7.588 × 10−3
Then the inner diameter of rod AB = 15.18 mm
Problem Number (3.21)
A torque of magnitude T = 900 N.m is applied at D as
shown. Knowing that the allowable shearing stress is 50 MPa in
each shaft, determine the required diameter of (a) shaft AB, (b)
shaft CD.

7. Solution:
𝜏 =
𝑇 𝐶
𝐽
, 𝐽 =
𝜋
2
𝐶4
𝑇𝑐
0.04
=
𝑇 𝐵
0.1
,
900
0.04
=
𝑇 𝐵
0.1
, 𝑇 𝐵 = 2250 𝑁. 𝑚
𝐶3
=
2𝑇
𝜋 𝜏
, 𝐶 𝐴𝐵 = √
2𝑇
𝜋 𝜏
3
= √
2 × 2250
3.14 × 50 × 106
3
= 0.031 𝑚
𝑇ℎ𝑒𝑛 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟 𝑜𝑓 𝑠ℎ𝑎𝑓𝑡 𝐴𝐵 𝑖𝑠 61.2 𝑚𝑚
𝐶 𝐷𝐶 = √
2𝑇
𝜋 𝜏
3
= √
2 × 900
3.14 × 50 × 106
3
= 0.0225 𝑚
𝑇ℎ𝑒𝑛 𝑡ℎ𝑒 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟 𝑜𝑓 𝑠ℎ𝑎𝑓𝑡 𝐷𝐶 𝑖𝑠 45 𝑚𝑚
Problem Number (3.22)
A torque of magnitude T = 900 N.m is applied at D as
shown. Knowing that the diameter of shaft AB is 60 mm and
that the diameter of shaft CD is 45 mm, determine the maximum
shearing stress in (a) shaft AB, (b) shaft CD.

8. Solution:
𝜏 =
𝑇 𝐶
𝐽
, 𝐽 =
𝜋
2
𝐶4
𝑇𝑐
0.04
=
𝑇 𝐵
0.1
,
900
0.04
=
𝑇 𝐵
0.1
, 𝑇 𝐵 = 2250 𝑁. 𝑚
𝜏 𝐴𝐵 =
2250 × 0.03
1.2717 × 10−6
= 53.078 𝑀𝑃𝑎
𝜏 𝐶𝐷 =
900 × 0.0225
4.024 × 10−7
= 50.33 𝑀𝑃𝑎
Problem Number (3.35)
The electric motor exerts a 500 N.m torque on the aluminum
shaft ABCD when it is rotating at a constant speed. Knowing
that G = 27 GPa and that the torques exerted on pulleys B and C
are as shown, determine the angle of twist between (a) B and C,
(b) B and D.
Solution:
𝜙 =
𝑇 𝐿
𝐺 𝐽
, 𝐽 =
𝜋
2
𝐶4
𝐽 𝐵𝐶 = 3.68 × 10−7

9. 𝜙 𝐵𝐶 =
800 × 1.2
27 × 109 × 3.68 × 10−7
= 0.097 𝑟𝑎𝑑 = 5.54 𝑜
𝐽 𝐶𝐷 = 5.21 × 10−7
𝜙 𝐶𝐷 =
500 × 0.9
27 × 109 × 5.21 × 10−7
= 0.032 𝑟𝑎𝑑 = 1.834 𝑜
𝜙 𝐵𝐷 = 𝜙 𝐶𝐷 + 𝜙 𝐵𝐶 = 5.54 + 1.834 = 7.374 𝑜
Problem Number (3.38)
The aluminum rod AB (G = 27 GPa) is bonded to the brass rod
BD (G = 39 GPa). Knowing that portion CD of the brass rod is
hollow and has an inner diameter of 40 mm, determine the angle
of twist at A.
Solution:
For Part AB:
𝜙 =
𝑇 𝐿
𝐺 𝐽
=
800 × 0.4
27 × 109 × 1.65 × 10−7
= 0.072 𝑟𝑎𝑑

10. For Part BC:
𝜙 =
𝑇 𝐿
𝐺 𝐽
=
2400 × 0.375
39 × 109 × 1.273 × 10−6
= 0.018 𝑟𝑎𝑑
For Part CD:
𝜙 =
𝑇 𝐿
𝐺 𝐽
=
2400 × 0.25
39 × 109 × 1.0205 × 10−6
= 0.0152 𝑟𝑎𝑑
Then 𝜙 𝐴 = 0.072 + 0.018 + 0.0152 = 0.1052 𝑟𝑎𝑑 = 6.03 𝑜