This document provides an overview of factorizing algebraic expressions. It discusses several methods of factorizing including finding common factors, regrouping terms, using factorizing identities, and dividing polynomials. Examples are provided to illustrate each method. The document is divided into seven parts covering factors of natural numbers, common factors, regrouping terms, factorizing identities, factors in the form of (x+a)(x+b), and dividing algebraic expressions.

1. FACTORISATIONFACTORISATION
KONDETI YASHWANT
Class – VIII “A”

2. PREVEIW
• PART1 :FACTORS OF NATURAL NUMBERS & AGEBRAIC EXPNS
• PART2 :METHOD OF COMMON FACTORS
• PART3: FACTORISATION BY REGROUPING TERMS
• PART4 :SOLVING SUMS ON FACTORIZING EXPNS
• PART5 :SOLVING SUMS ON FACTORISATION USING IDEN
• PART6 :FACTORS OF THE FORM (x+a)(x+b)
• PART7 :DIVISION OF ALGEBRAIC EXPNS

3. Introduction
Factors of natural numbers
e.g. 90 = 2 x 3 x 3 x 5
Factors of algebraic expressions
Terms are formed as product of factors.
e.g. 5xy = 5 x x x y
10x(x+2)(y+3)=2x5xxx(x+2)x(y+3)

4. Method of common factors
• We write each term as a product of
irreducible factors. Then take out the common
factors of the terms and write the remaining
factors to get the desired factor form.
• E.g. 5ab+10a
(5xaxb)+(10xa)
(5axb) + (5ax2)
5a( b+2 ) (desired factor form)

5. Factorisation by regrouping terms
• Regrouping is re-arranging the terms with common
terms.
e.g. 1) a2
+ ab + 8a + 8b
a(a+b) + 8(a+b)
(a+b) (a+8)
2) 15ab – 6a + 5b – 2
3a(5b-2) + 1(5b-2)
(3a+1) (5b-2)

6. Let us solve some examples

7. 5m2
n – 15mn2
5mn ( m -3n)
5 x m x n x(m-3n)

8. Factorise
a2
bc + ab2
c + abc2
Take the common factors
abc ( a + b +c )
a x b x c x (a + b + c)

9. Factorise
15pq + 15 + 9q + 25p
• Regrouping like terms to find common factors
15pq + 9q + 25p +15
3q ( 5p + 3 ) + 5 ( 5p + 3 )
(3q + 5) (5p + 3)

10. Factorisation using identities
• Observe the expression.
• If it has a form that fits the right hand side of one of the identities , then
the expression corresponding to the left hand side of the identity gives
the desired factorisation.
• (a+b)2
= a2
+2ab+b2
• (a-b)2
= a2
-2ab+b2
• (a2
-b2
) = (a+b)(a-b)

11. Few examples
• 1) p2
+ 8p + 16
It is in the form of the identity a2
+2ab+b2
therefore
p2
+ 2 (p) (4) + 42
Since a2
+ 2ab +b2
= (a+b)2
By comparison
p2
+ 8p + 16 = ( p + 4)2
( required factorisation )

12. Factorise
• 49p2
– 36
(7p)2
– (6)2
(7p+6) (7p-6)
•a2
– 2ab +b2
– c2
(a-b)2
– c2
(a-b-c) (a-b+c)

13. Factors of the form (x+a)(x+b)
• In general , for factorising an algebraic expression of the type
x2
+px+q , we find two factors a and b of q (i.e. the constant
term) such that
ab = q
a+b = p

14. 4 2 2 4
2 2 2 2 2 2
2 2 2
2
( ) 2 ( )
( )
a a b b
a a b b
a b
− +
− +
+

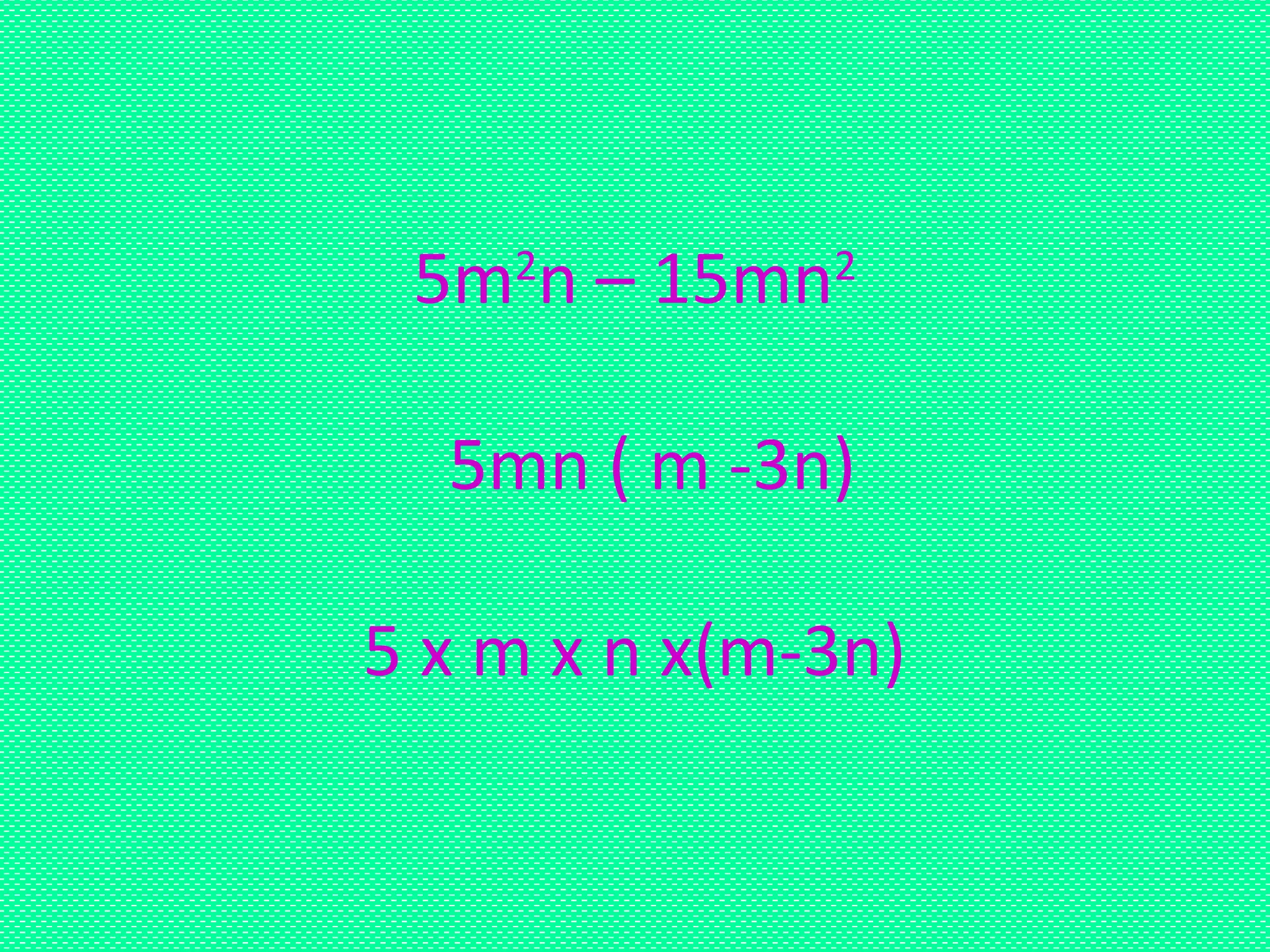
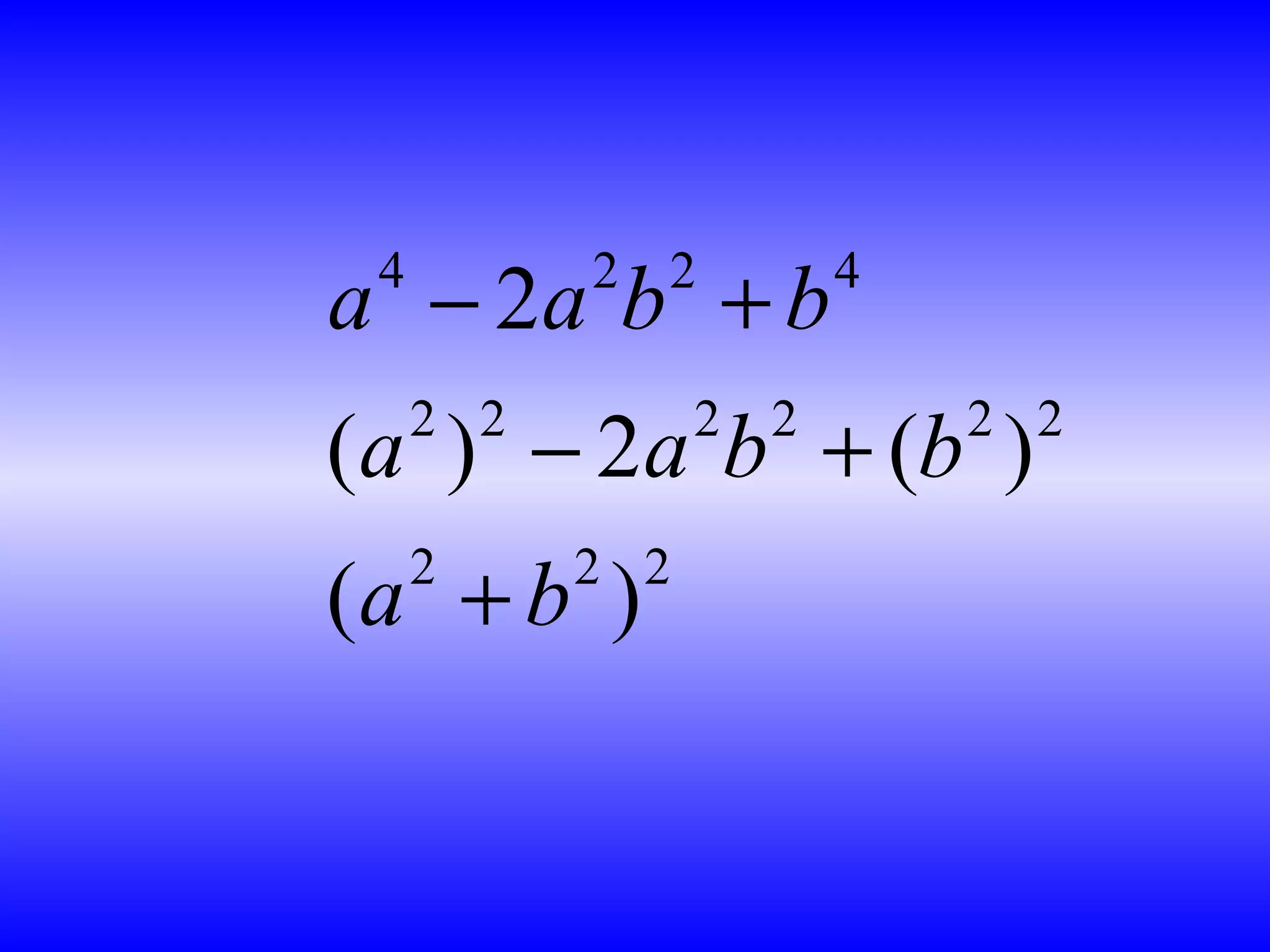
15. 2
2
2
2
4 8 4
4( 2 1)
4( 1)
4[ ( 1) 1( 1)]
4( 1)( 1)
4( 1)
x x
x x
x x x
x x x
x x
x
− +
− +
− − +
− − −
− −
−

16. 2
2
6 8
4 2 8
( 4) 2( 4)
( 2)( 4)
p p
p p p
p p p
p p
+ +
+ + +
+ + +
+ +

17. 2
2
10 21
7 3 21
( 7) 3( 7)
( 7)( 3)
a a
a a a
a a a
a a
− +
− − +
− − −
− −

18. Division of algebraic expressions
• Division of monomial by another monomial
• Division of polynomial by a monomial
• Division of polynomial by polynomial

19. Division of monomial by another
monomial
3
6 2x x÷
Now let us write the irreducible factor forms
3
3
2
3 2
6 2 3
2 2
6 2 (3 )
(2 ) (3 )
6 2 3
x x x x
x x
x x x x
x x
x x x
= ×× × ×
= ×
∴ = × × × ×
= ×
∴ ÷ =

20. Division of polynomial by a monomial
2
(5 6 ) 3
(5 6)
3
(5 6)
3
x x x
x x
x
x
− ÷
−
×
−

21. 3 2
2
2
( 2 3 ) 2
( 2 3)
2
( 2 3)
2
x x x x
x x x
x
x x
+ + ÷
+ +
×
+ +

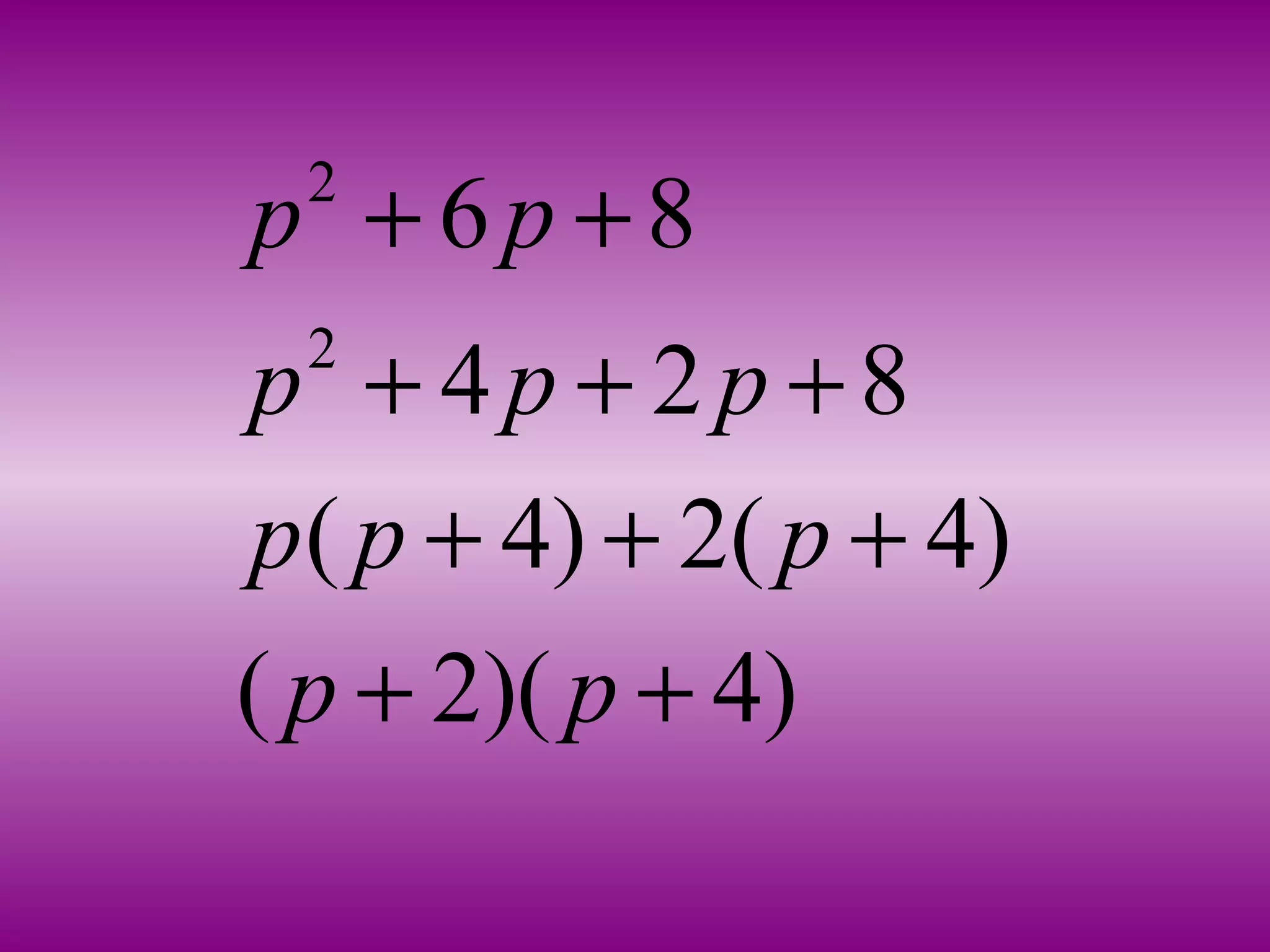
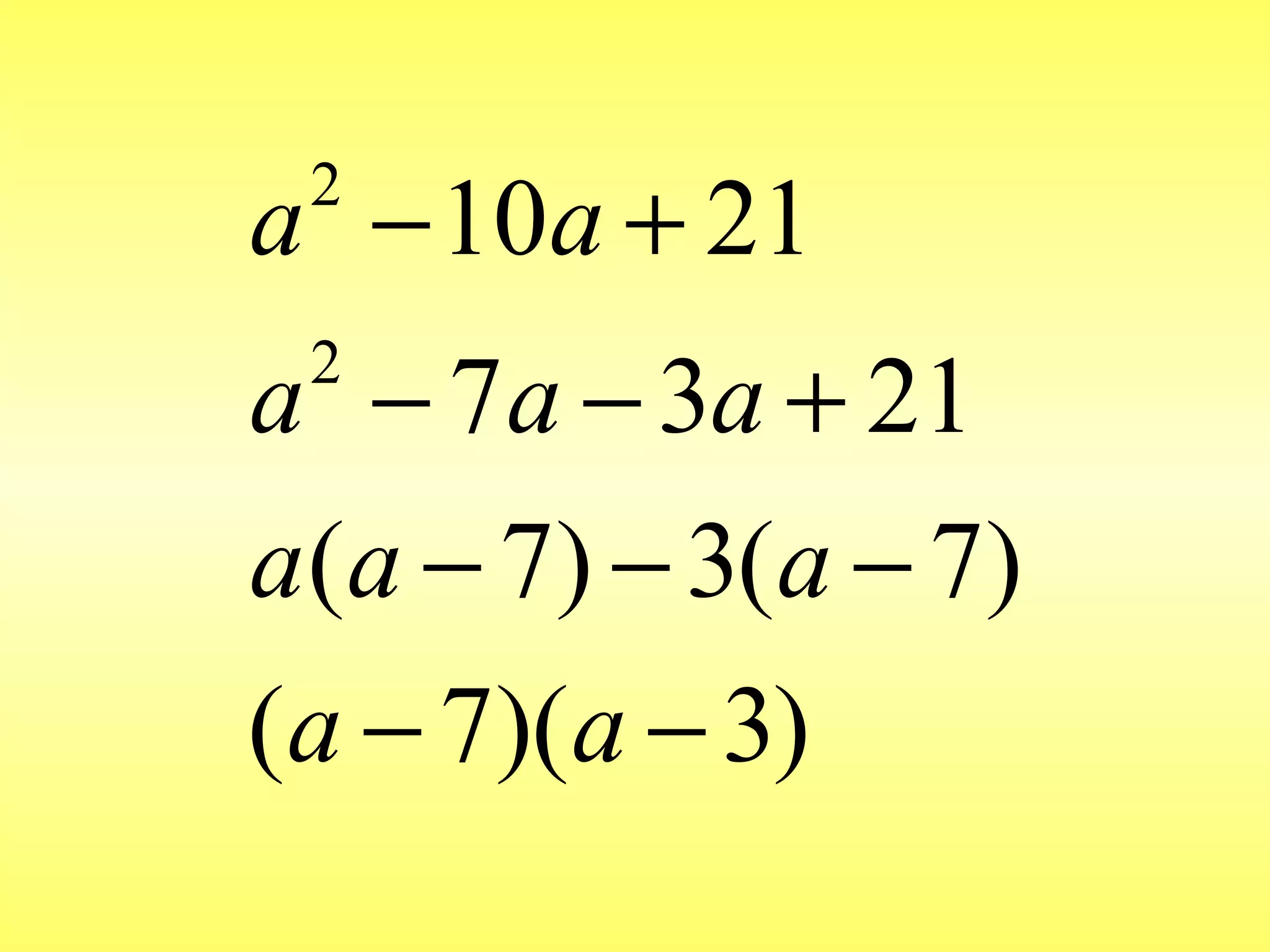
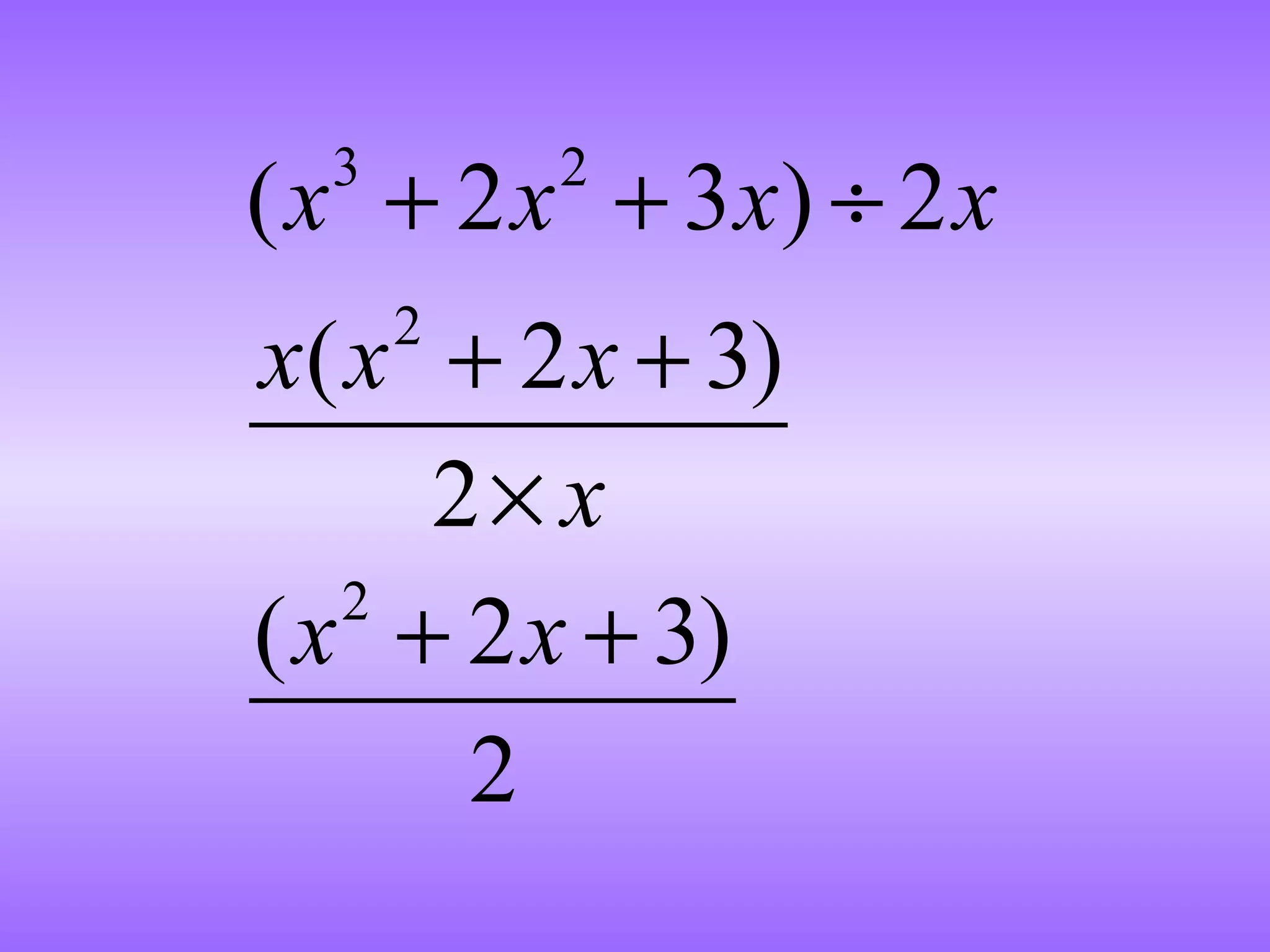
22. Division of polynomial by polynomial
2
2
( 7 10) ( 5)
( 5 2 10)
( 5)
[ ( 5) 2( 5)]
( 5)
( 5)( 2)
( 5)
( 2)
y y y
y y y
y
y y y
y
y y
y
y
+ + ÷ +
+ + +
+
+ + +
+
+ +
+
+

23. 2
2
( 14 32) ( 2)
( 16 2 32)
( 2)
[ ( 16) 2( 16)]
( 2)
( 16)( 2)
( 2)
( 16)
m m m
m m m
m
m m m
m
m m
m
m
− − ÷ +
− + −
+
− + −
+
− +
+
−