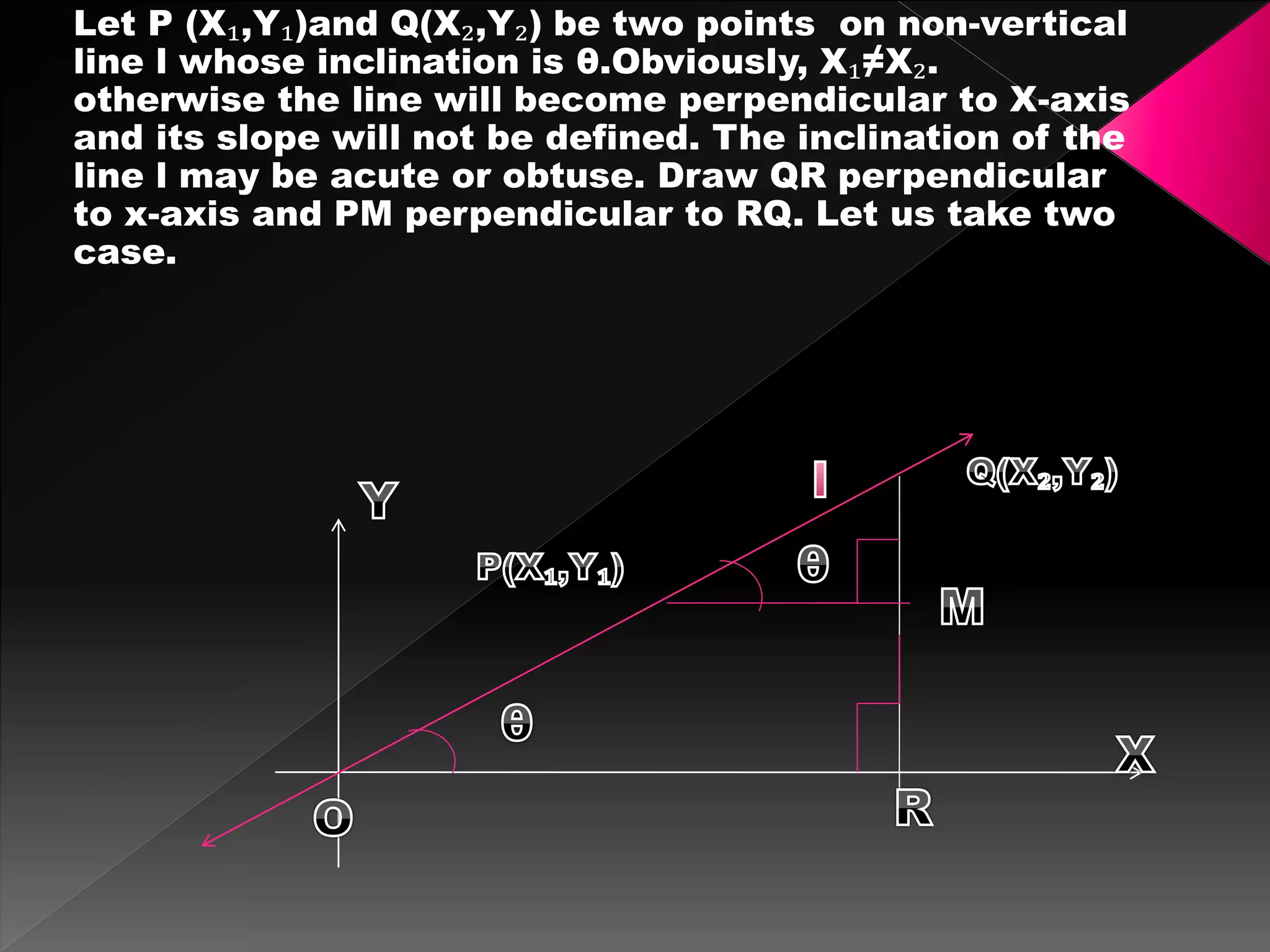
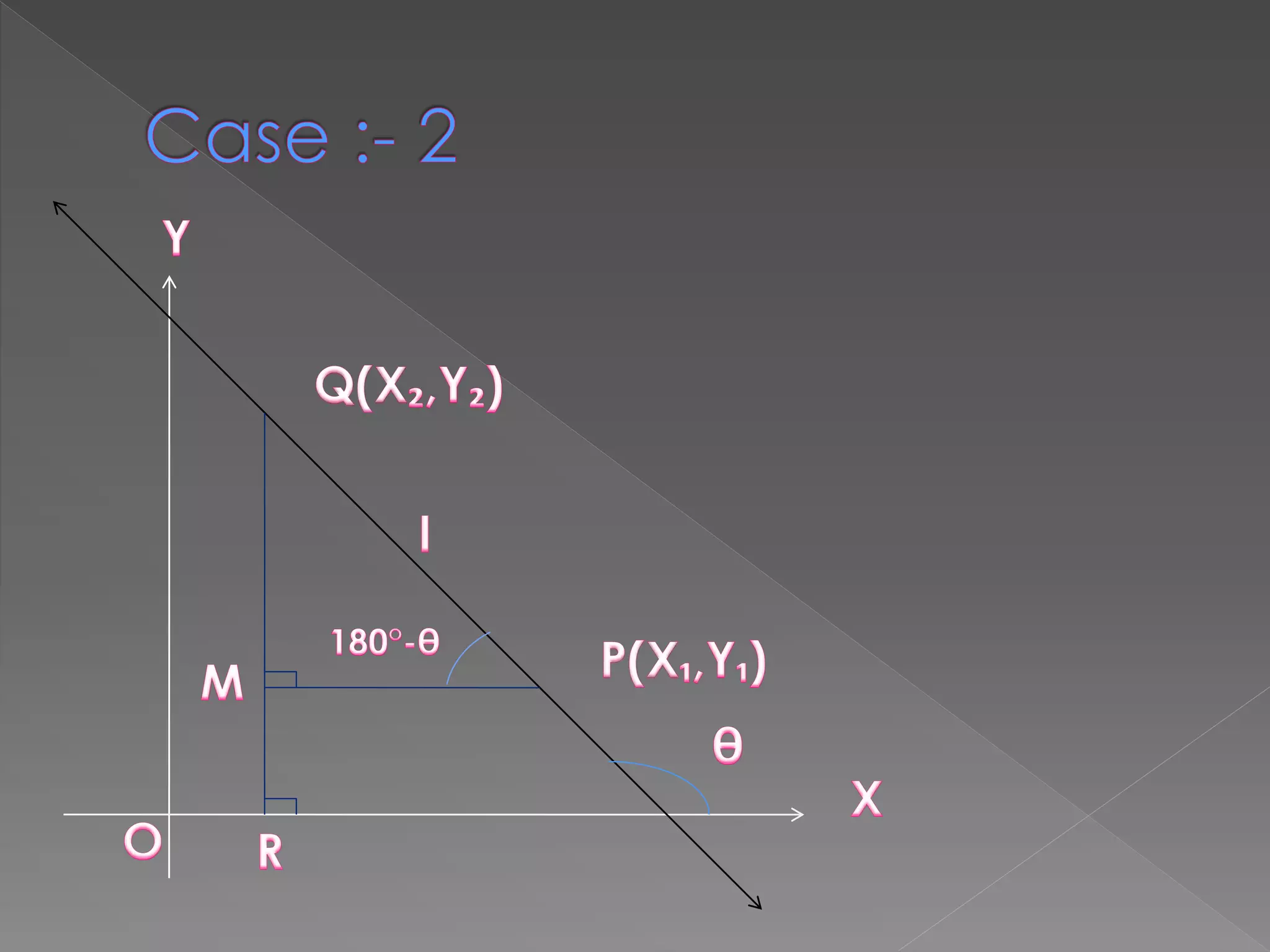
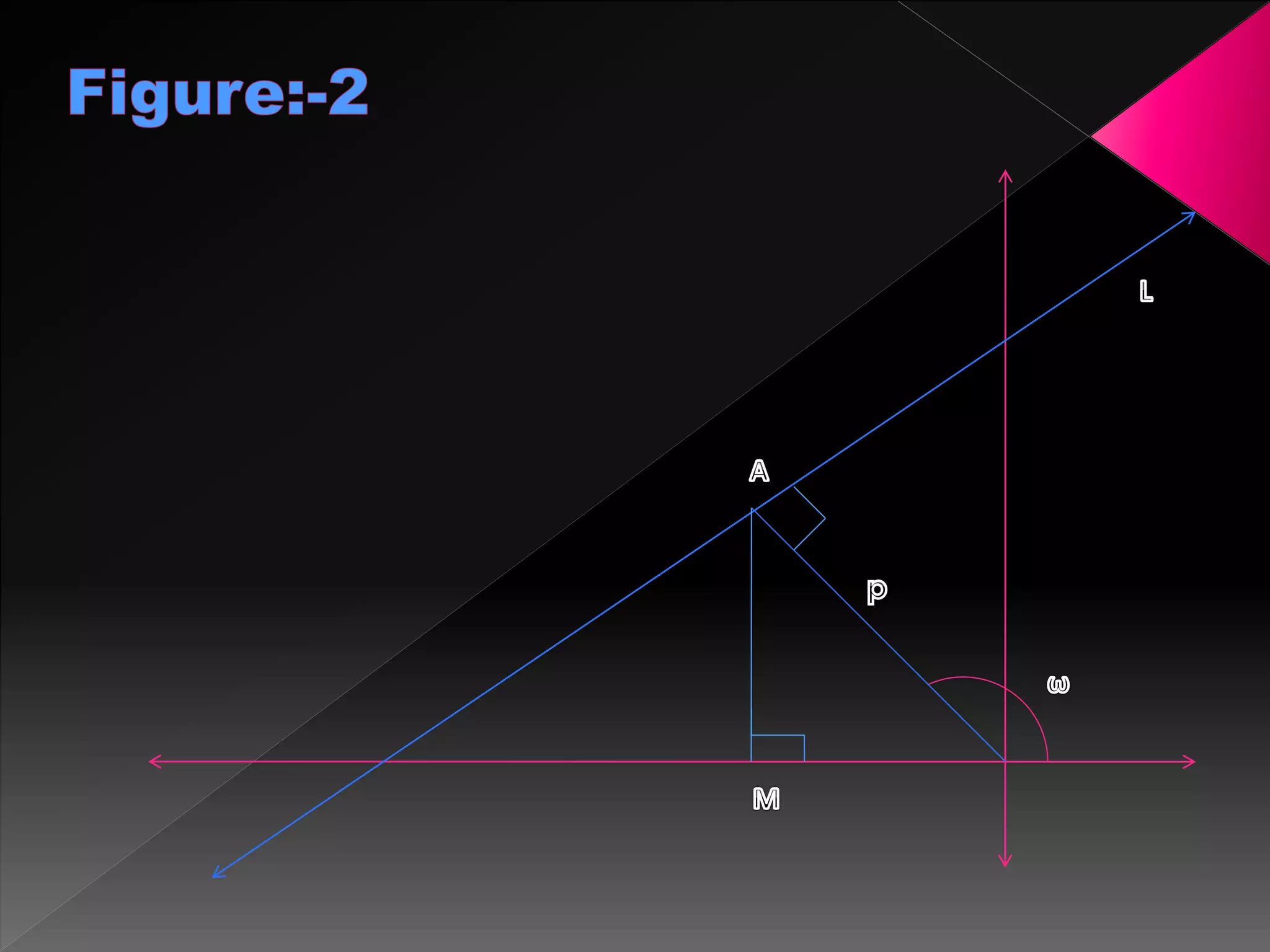
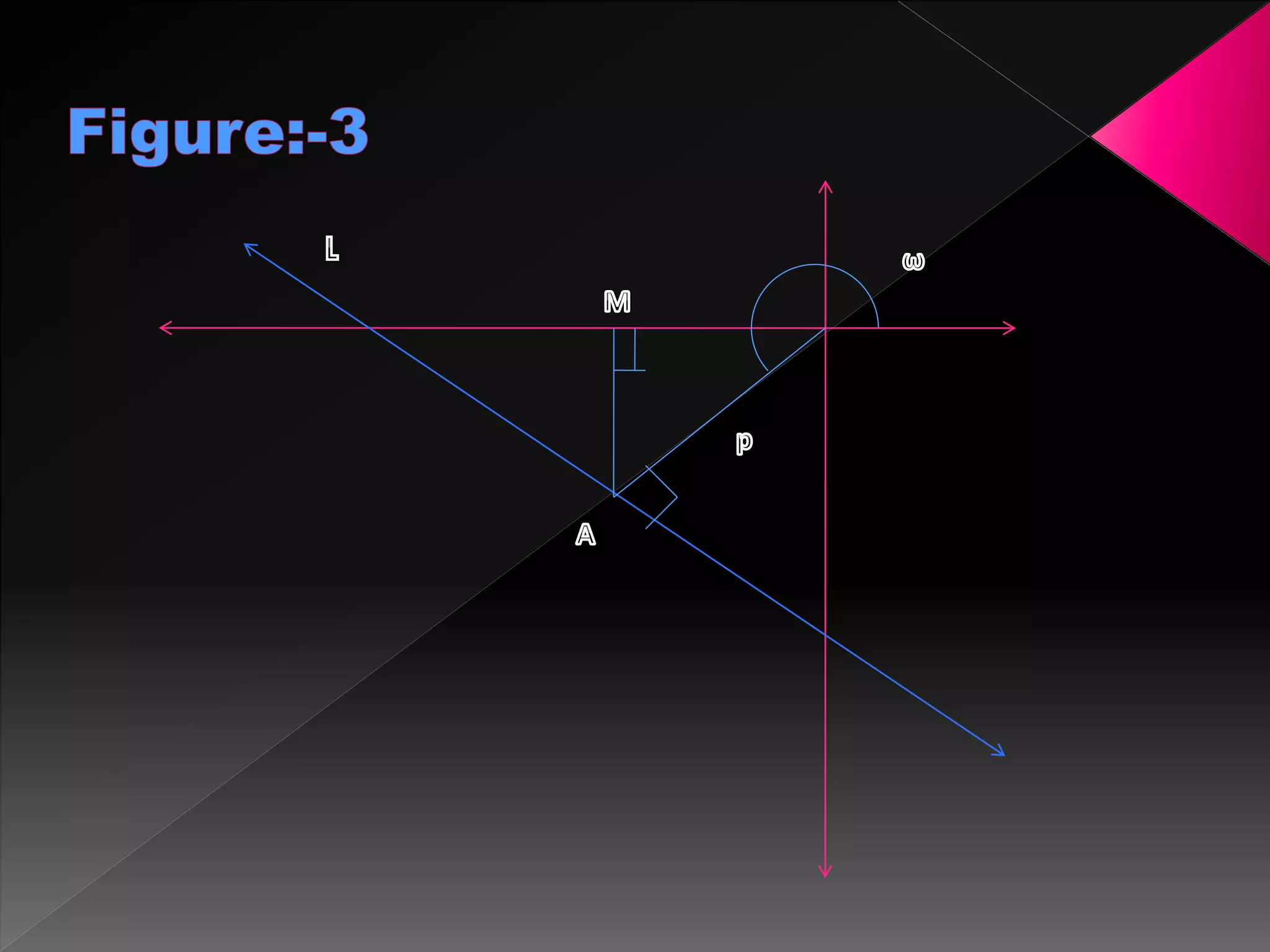
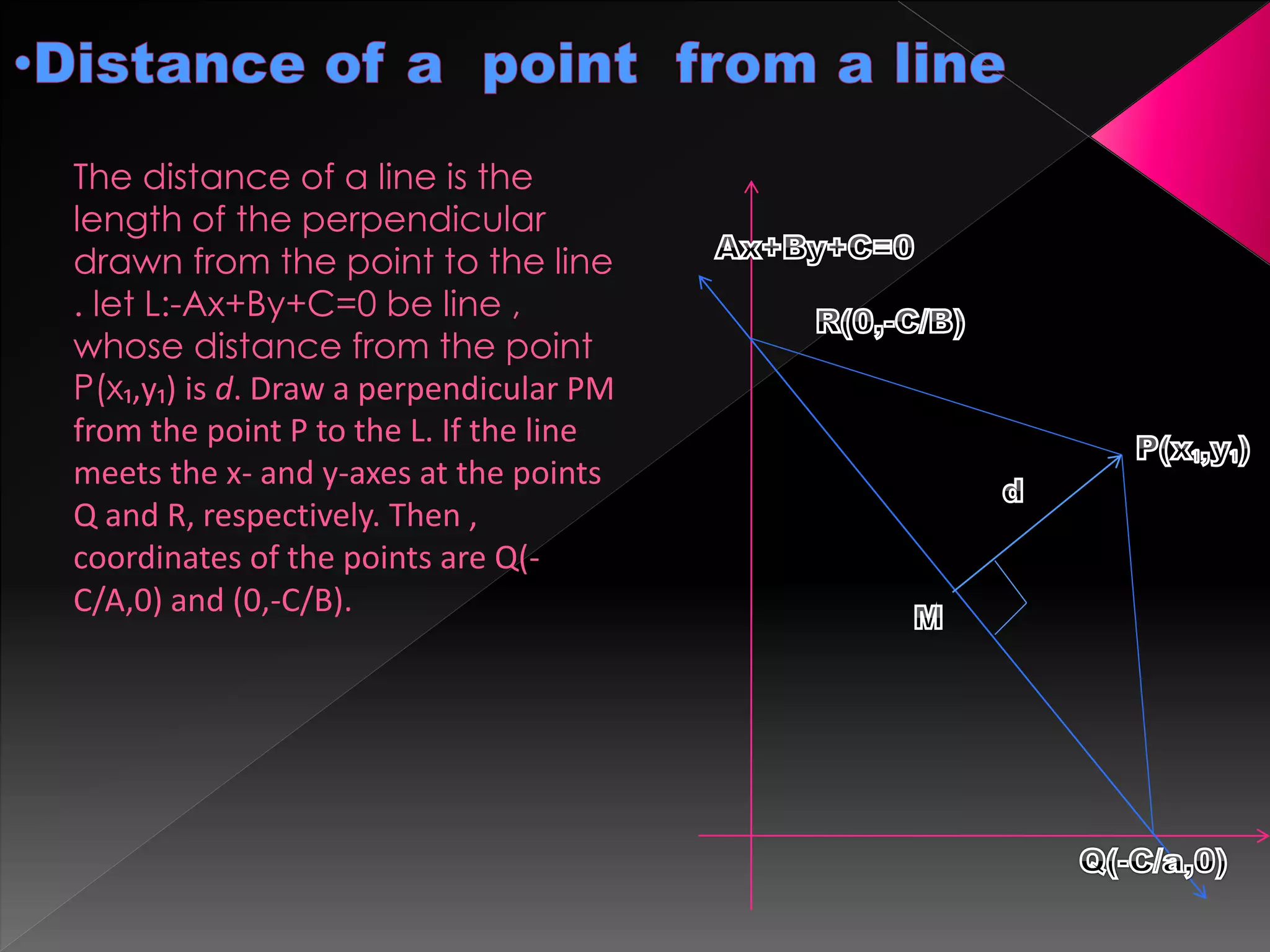
The document discusses various topics related to lines in a coordinate plane including: 1) How to find the slope of a line given two points on the line. The slope is defined as the rise over the run between the two points. 2) The different forms of the equation of a line including slope-intercept, two-point, and normal forms. 3) How to find the distance between a point and a line, between two parallel lines, and the intercepts of a line with the x and y axes.

2. 1. Coordinate axes
2. Coordinate plan
3. Plotting of points in plane
4. Distance between two points
5. Section Formula

3. 1. If θ is the inclination of a line
L,then θ is called the slope or
gradient of the line L.
2. The slope of a line is denoted by
m. Thus,m=tan θ,θ≠90°

6. Let P (X₁,Y₁)and Q(X₂,Y₂) be two points on non-vertical
line l whose inclination is θ.Obviously, X₁≠X₂.
otherwise the line will become perpendicular to X-axis
and its slope will not be defined. The inclination of the
line l may be acute or obtuse. Draw QR perpendicular
to x-axis and PM perpendicular to RQ. Let us take two
case.

7.  When angle θ is acute:
In fig, MPQ=θ.
Therefore,slope of line l=m=tanθ.
.......(1)
 But in ∆MPQ,we have tanθ=MQ/MP
= Y₂-Y₁/X₂-X₁ ..........(2)
From (1) &(2),we have
m= Y₂-Y₁/X₂-X₁

9.  When angle θ is obtuse: In fig, we have
m=tanθ
MPQ=180°-θ.
Therefore,θ=180°- MPQ
Now, slope of line
=tan(180°- MPQ)
=-tan MPQ=- MQ/MP
= - (Y₂-Y₁)/(X₁-X₂)
= Y₂-Y₁/X₁-X₂
Consequently, we see that in the both cases the
slope m of line through the points (X₁,Y₁)&(X₂,Y₂) is
given by m= Y₂-Y₁/X₁-X₂

10. •If the line l is parallel to L then their
inclinations are equal,i.e..,
=β,and hence,
tan =tanβ
Therefore m₁=m₂, i.e.,their slopes are
equal.
Conversly,if the slope of two lines l₁ & l₂ is
same,i.e., m₁=m₂
Then tan =tanβ
By property of tangent function
(between 0° & 180° , =β.
Therefore,the line are parallel if and only
if their slopes are equal.

11. If the lines L & l are perpendicular then
β= + 90°.
Therefore,
tan β =tan( + 90°)
= -cot
= - 1/tan
i.e., m₂=- 1/m₁
or m₁.m₂=-1
Conversely, if m₁.m₂ =-1, i.e,tan tanβ=-1
Then
tanβ=cotβ=tan(β+90°)
or tan(β-90°)
Therefore &β differ by 90°.
Hence, two non vertical lines are
perpendicular to each other if and only if
their slopes are negative
reciprocals of each other.

12. Let L₁ & L₂ be two non vertical lines with slopes m₁ &
m₂ respectively. if &β are the inclination of lines
L₁&L₂ respectively. Then
m₁=tan ₁ & m₂=tan ₂.
Let θ & be adjacent angles between the line L₁
& L₂. Then θ= ₂- ₁ & ₁, ₂≠90°.
Therefore
tanθ=tan( ₂- ₁)
=tan ₂-tan ₁/1+tan ₁tan ₂
=m₂-m₁/1+m₁m₂
And =180°-θ
tan =tan(180°-θ)
= - (m₂-m₁)/1+m₁m₂
Now there arise two cases.

13. If tanθ is positive, then tan will be negative,
which means that θ will be acute and will
be obtuse.
If tanθ is negative,then tan will be positive,
which means that θ will be obtuse and will
be acute.
Thus, for solve problem we use tanθ=│m₂-
m₁/1+m₁m₂│.

14. We know that slopes of two parallel lines are equal. If two lines having
the same slope pass through a common point, then two lines will
coincide.hence,if A,B &C are three points in the XY plane, then they will
lie on a line ,i.e., three points are collinear if and only slope of AB= slope
of BC

16. If a horizontal line L is distance a from the X-axis then ordinate of every
point lying on the line is either a or –a. Therfore,equation of line L is either
y=a or y=-a. sign will depend upon the position of the line according as the
line is above or below the y-axis. Similarly, the equation of a vertical line at a
distance b from the y-axis is either x=b or x= -b.

17. Suppose that P₀(X₀,Y₀) is a fixed point on a
non-vertical line L,whose slope is m.Let
P(X,Y)be an arbitrary point on L.
Then, by definition , the slope of L is given by
m=Y-Y₀/X-X₀
Y-Y₀=m(X-X₀) …(1)
Since the point P₀(X₀,Y₀) along with all
points (X,Y) on L satisfies (1) and no other
point in plane satisfies (1).Equation (1) is
needed the equation for the given line L.
Thus, the point (X,Y) lies on the line with
slope m through the fixed point(X₀,Y₀), if and
only if, its coordinates satisfies the equation
Y-Y₀=m(X-X₀)

18. Let the line L passes through two given
points P₁(X₁,Y₁) and P₂(X₂,Y₂). Let P(X,Y)
be a general point on L.
The three points P₁,P₂ & P are collinear ,
therefore, we have slope of
P₁P=slope of P₁P₂
i.e., Y-Y₁/X-X₁=Y₂-Y₁/X₂=X₁
Thus , equation of the line passing
through the points (X₁,Y₁) and (X₂,Y₂) is
given by
Y-Y₁/X-X₁=Y₂-Y₁/X₂-X₁

20. Suppose a line L with slope m cuts the y-axis
at a distance c from the origin. The distance
c is called the y-intercept of the line L.
obvisouly,coordinate
of the point where the line meet they-axis
are (0,c).
Thus , L has slope m and passes through a
fixed point (0,c).
Therefore , by point-slope form, the equation
of L is
y-c=m(x-0) or y=mx+c
Thus, the point (x,y) on the line with slope m
and y-intercept c lies on the line if and only
if
y=mx+c

21. •Suppose line L with slope m makes x-intercept d. Then
equation of L is
y=m(x-d)

22. Suppose a line L makes x-
intercept a and y-intercept b on
the axes.Obivously L meets x-
axis at point (0,b) . By two form
of the equation of the line we
have
y-0=b-0/0-a. (x-a)
Thus, equation of the line
making intercepts a and b on x-
axis and y-axis , respectively, is
x/a+ y/b=1

23. Suppose a non vertical line is known to us with following
data:
(1)Length of the e perpendicular from origin to the line.
(2)Angle which normal makes with the positive direction of
x-axis
Let L be the line, whose perpendicular distance from origin
O be OA=p and the angle between the positive to
perpendicular x-axis and OA be XOA=ω. The possible
position of the L in the Cartesian plan. Now , our purpose is
to find slope of L and a point on it. Draw perpendicular AM
on the x-axis in each case.

28. In each case, we have OM=pcosωand MA=psinω, so that the
coordinates of the point A.
Further , line L is perpendicular to OA.Therefore
the slope of the line L=- 1/slope of OA
=- 1/tanω
= - cosω/sinω.
Thus, the line L has slope -cosω/sinω and point A on it.
Therefore , by point slope form , the equation of the line L is y-
p sinω = - cos ω/ sinω(x-p cosω)
x.cosω + y sinω=p
Hence, the equation of the line having normal makes distance
p from origin and angle ω which the normal makes with the
positive direction of x-axis is given by
x.cosω + y.sinω=p

29. Ax+By+C=0 is general form equation of a line

30. •If B≠0,then Ax+By+C=0 can be written as
y=-A/B.x-C/B or y=mx+c ………(1)
where m=-A/B and c=-C/B.
we know that equation (1) is the slope intercept form of the
equation of a line whose slope is -A/B and y-intercept is –C/B.
If B=0,then x=-C/A, which is vertical line whose slope is
undefined and x-intercept is –C/A.

31. If C≠0,then Ax+By+C=0 can be written as x +
y = 1
-C/A -C/B
a=-C and b=-C
A B
we know that equation is the intercept form of the
equation of a line whose x-intercept is –C/A and y-
intercept is –C/B.
If C=0,then Ax+By+C=0 can be written as
Ax+By+C=0,which is a line passing through the origin
and, therefore , has zero intercept on the axis.

32. Let x cosω+ y sinω=p be the normal form of the line represented
by the equation Ax+By+C=0 or Ax+By=-C. Thus, both the equation
are same and therefore, A = B =-C
cosω sinω p
which gives cosω=-Ap/C and
sinω =-Bp/C.
Now,
sin² ω + cos² ω=(-Ap/C)² + (-BP/c)²=1
p²= C² or p=± C .
A²+B² √A²+B²
Therefore cosω=± A and
√A²+B²
Sinω=± B .
√A²+B²
Thus ,the normal form equation is xcosω+Ysinω=p

33. The distance of a line is the
length of the perpendicular
drawn from the point to the line
. let L:-Ax+By+C=0 be line ,
whose distance from the point
P(x₁,y₁) is d. Draw a perpendicular PM
from the point P to the L. If the line
meets the x- and y-axes at the points
Q and R, respectively. Then ,
coordinates of the points are Q(-
C/A,0) and (0,-C/B).

34. •Thus ,the area of the triangle PQR is given by
area(∆PQR)=½PM.QR
PM=2area (∆PQR)
QR ………(1)
also, area(∆PQR)
=½│x₁(0+C/B)+(-C/A)(-C/B-y₁)+0(y₁-0)│
=½│x₁.C/B + y₁.C/A+C²/AB│
2 area (∆PQR)=│C/AB│.│AX₁+By₁+C│, and
QR= (0+C/A)²+ (C/B-0)²
= │C/AB│.√A²+B²
Substituting the values of area(∆PQR) and QR in (1) , we get
PM=│Ax₁+By₁+C│/√ A²+B²
d = │Ax₁+By₁+C│/√ A²+B².

35. We know that slopes of two parallel lines are equal.
Therefore , two parallel lines can be taken in the form y=mx+c₁ …
(1)
y=mx+c₂ ….(2)
Line (1) will be intersect x-axis at point A(-c₁/m,0) .
Distance between two lines is equal to the length of perpendicular
from point A to line(2).Therefore , distance between the lines (1)
and (2) is
│(-m)(-c₁/m)+(-c₂)│/√1+m²
d= │c₁-c₂│/ √1+m²
Thus , the distance d between two parallel line
y=mx+c₁ and y=mx+c₂ is given by
d= │c₁-c₂│/ √1+m²
If lines are given form , i.e. , Ax+By+C₁=0 & Ax+By+C₂=0 then
d=│c₁-c₂│/√A²+B².