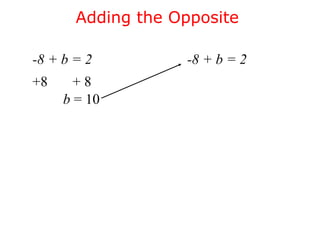
This document discusses solving one-step linear equations using addition and subtraction. It defines key terms like equations, solutions, and isolating variables. It explains that when transforming equations, the same operations must be applied to both sides to maintain equivalence. Inverse operations like addition and subtraction can isolate variables. Examples show how to isolate variables using addition or subtraction and solve equations. Students are then prompted to solve practice equations on their own. The document also discusses using equations to solve real-world problems, like finding a person's maximum heart rate based on their age.

1. 2-1 – Solving Equations Using
Addition and Subtraction

2. 2-1 – Solving Equations Using
Addition and Subtraction
Goals:
1. I can solve one step linear equations
using addition and subtraction.
2. I can use linear equations to solve
real-life problems such as finding a
record temperature.

3. Special Vocab (notebook please…
Equation – a mathematical statement that two expressions are
equal.
A solution of an equation is a value of the variable that makes
the equation true.
To find solutions, we isolate the variable. A variable is
isolated when it appears by itself (no coefficients) on one side
of the equation.

4. Solving Equations Basics
When transforming equations (isolating the variable) – they
must remain balanced! Whatever you do to one side of the =
sign, you MUST do to the other side!

5. Inverse Operations – are operations that undo each other, such
as addition and subtraction. Inverse operations help you
isolate the variable in an equation.
* Do the opposite to “undo” an equation!
 If you are adding TO the variable – then subtract.
 If subtracting FROM the variable – then add.
 Sometimes you have to add the opposite……
 If multiplying TO the variable, then divide!
 If DIVIDING the variable by something, then multiply
by the reciprocal!

6. Transformations that Produce
Equivalent Equations
Add the same
number to each
side.
Original Equation Equivalent Equation
x – 3 = 5 x = 8
Subtract the same
number from
each side.
x + 6 = 10 x = 4
Simplify one or
both sides. x = 8 - 3 x = 5
sides. 7 = x x = 7
Interchange the
Add 3
Subtract 6
Simplify
Interchange

7. Properties of Equality
Addition Property of Equality – You can add the same
number to both sides of an equation, and the statement will
still be true.
Numbers Algebra
3 = 3 a = b
3 + 2 = 3 + 2 a + c = b + c
5 = 5

8. Properties of Equality
Subtraction Property of Equality – You can subtract the
same number from both sides of an equation, and the
statement will still be true.
Numbers Algebra
7 = 7 a = b
7 - 5 = 7 - 5 a - c = b - c
2 = 2

9. Solution Steps
Each time you apply a transformation to an equation, you are
writing a solution step. Solution steps may be written one
below each other with the equal sign aligned.
Survival tip: SHOW your solution steps – it makes checking
your work easier and your grade higher! This may not seem
important now, but when have you much more complex
equations, you will need that skill. (BTW – this is not
optional).

10. Examples – Using addition to solve
x – 9 = -17
+ 9 = +9
x = -8
x – 9 = -17
-8 – 9 = -17
-17 = -17
Now try….. And check: x – 12 = 13

11. Your turn
n – 3.2 = 5.6
-6 = k - 6

12. Examples – Using subtraction to
solve
x + 12 = 15
- 12 = -12
x = 3
x +12 = 15
3 + 12 = 15
15 = 15
Now try….. And check: -5 = k +5

13. Your turn
1 1
2 2
d + =
6 + t =14

14. Adding the Opposite
-8 + b = 2
+8 + 8
b = 10
-8 + b = 2

15. Your turn
-2.3+ m = 7
3 11
4 4
- + z =

16. Examples – Simplifying First
-9 = n – (-4)
-9 = n + 4
- 4 = -4
-13 = n
-9 = n – (-4)
-9 = -13 – (-4)
-9 = -13 +4
-9 = -9

17. Your Turn
-11 = n – (-2)

18. Your turn
2 - (-b) = 6

19. Real World Problem
A person’s maximum heart rate, is the highest rate,
in beats per minute that the person’s heart should
reach. One way to estimate maximum heart rate
states that your age added to your maximum heart
rate is 220. Using this method, write and solve an
equation to find the maximum heart rate of a 15 year
old.
- Then use this method to find Mr. Hedges’ age if his
maximum heart rate is 168.

20. Quick Review
What are Equivalent Equations?
What are inverse operations? Give me an example.

21. 2-1 – Homework
P80, 22 - 74 even