This document provides an overview of the Ohio Department of Transportation's (ODOT) pavement design method. It discusses the basic factors considered in design, including serviceability, subgrade characterization, traffic loading, reliability, and drainage. The ODOT method is based on the American Association of State Highway and Transportation Officials (AASHTO) Guide, using a regression relationship between load cycles, pavement structural capacity, and performance. It considers traffic loads in terms of equivalent single axle loads and uses reliability levels depending on road importance. Rigid and flexible pavement designs are outlined, including parameters considered and thickness design processes. Limitations of the current ODOT method are also discussed.

1. Critical Appraisal of Pavement Design of
Ohio Department of Transportation
(ODOT)
Presented by
Pranamesh Chakraborty
Sharath M N
Indian Institute of Technology,
Kanpur
13 April 2013

2. Basis of Pavement Design Manual
The ODOT method for pavement design is
almost identical to the American Association
of State Highway and Transportation Officials
(AASHTO) Guide for Design of Pavement
Structures (1993).

3. Basic factors in pavement design
1. Serviceability/Pavement performance
expressed in terms of Present Serviceability
Rating (PSR).
2. Subgrade Soil Characterization
(expressed in terms of Subgrade Resilient
Modulus (MR)).
3. Traffic (expressed in terms of Equivalent
Single Axle Load ESAL).
4. Reliability
5. Drainage

4. Approach in pavement design
There are three basic approach for Pavement design
1. Empirical Approach
2. Mechanistic Approach
3. Mechanistic –Empirical Approach
ODOT/AASHTO method is an empirical
method based on the AASHO Road Test from
the late 1950s .

5. ODOT method
The ODOT design method is a regression relationship
between
1. # of load cycles
2. Pavement Structural capacity
3. Performance (measured in terms of serviceability)
Disadvantages of regression methods
Limitation of Application
Can be applied to conditions similar to those
for which they were developed.

6. Serviceability
The concept of serviceability is supported by four
fundamental assumptions:
1. Highways are for the comfort of the travelling
user;
2. The user’s opinion as to how a highway should
perform is highly subjective;
3. There are characteristics that can be measured and
related to user’s perception of performance;
4. Performance may be expressed by the mean
opinion of all users;

7. Structural  Cracking, faulting, raveling, etc.
Functional  Riding comfort (measured in terms of
roughness of pavement.)
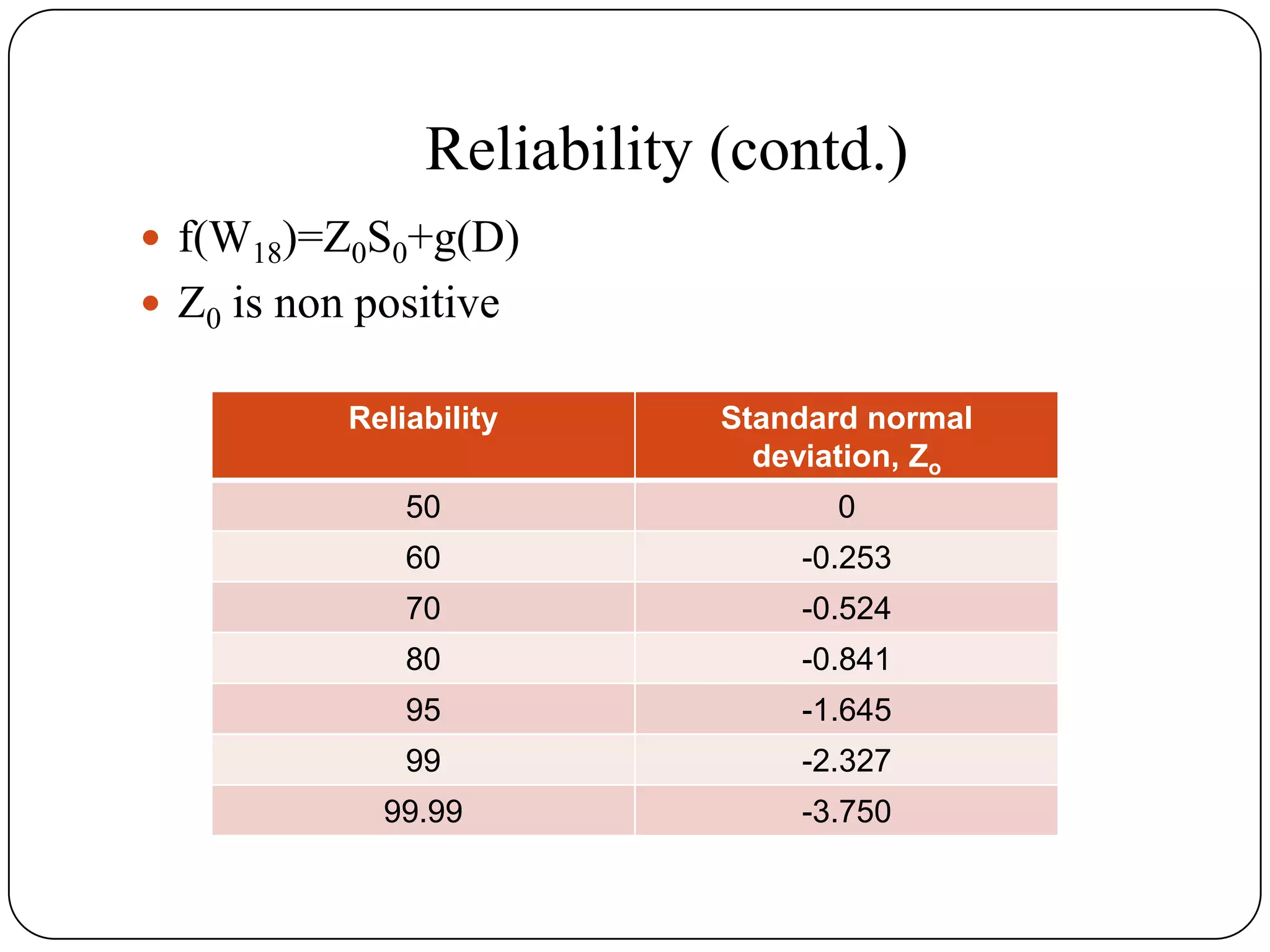
Serviceability Performance: Measured by PSI  Present
Serviceability Index with scale 0 to 5.
0 "Road closed"
5 "Just constructed" Initial PSI (pi) [4.2 (rigid)
and 4.5(flexible)]
Terminal PSI (pt)
 2.5 to 3.0 for major highways
 2.0 for lower class highways
 1.5 for very special cases
PSI
Serviceability (contd.)

8. Serviceability (contd.)
Serviceability cannot be directly measured in the field.
Panel of users required to provide subjective assessments of serviceability
known as Present Serviceability Ratio (PSR).
The correlation of PSR with measured distresses is the Present Serviceability
Index (PSI).
However, PSI is the input parameter of the design equation, not the PSR,
because determining PSR is very subjective.
 Alternative approaches are available correlating PSI with roughness, (Al-
Omari and Darter, 1994; Gulen et al., 1994) which is a more reliable, and
more easily measured parameter than the recommended distresses like mean
rut depth, cracking, patching, etc.

9. Traffic calculation
Traffic is considered in terms of ESAL.
The first step in calculating ESALs for mixed traffic is to
establish first the load equivalent factor (LEF) of every axle
of the traffic distribution.
The LEFs consider the following variables:
Axle load
 Axle configuration (e.g., single, tandem, etc.)
 Structural number (for flexible pavements)
 Terminal serviceability
LEFs were developed based on empirical data obtained from
the AASHO Road Test.

10. Traffic calculation (contd.)
With LEF calculated for every load group, the second step is to compute the
truck factor Tf as follows:
Tf = Ʃ(pi LEFi ) A
in which:
pi = percentage of repetitions for ith load group
LEFi = LEF for the ith load group (e.g., single-12kip, tandem-22kip, etc.)
A = average number of axles per truck
The number of ESALs is calculated as follows:
ESAL = AADT T Tf G D L 365 Y
in which:
D= trucks in design direction (%)
L = trucks in design lane (%)
AADT = annual average daily traffic
T = percentage of trucks
G = growth factor
D = trucks in lane (%)
Y = design period

11. Discussion on Traffic calculation
It relies on a single value to represent the overall traffic
spectrum which is questionable.
The LEFs consider serviceability as the damage equivalency
between two axles.
Zhang et al. (2000) have found that LEFs determined by this,
is inconsistent with capturing damage in terms of equivalent
deflection, which is easier to measure and validate.
However quantifying damage equivalency in terms of
serviceability or even deflections is not enough to represent the
complex failure modes of pavements.

12. Reliability
 R=p(Napp<nf)
 Considers the expected traffic to be normally
distributed
 R=f(ZoSo)
 Reliability level required is dependent on importance
of the road
 Overall standard deviation=0.39

13. Reliability (contd.)
 f(W18)=Z0S0+g(D)
 Z0 is non positive
Reliability Standard normal
deviation, Zo
50 0
60 -0.253
70 -0.524
80 -0.841
95 -1.645
99 -2.327
99.99 -3.750

14. Rigid Pavement Design
 Design Parameters
 Modulus of Rupture 700 psi
 Modulus of Elasticity 5,000,000 psi
 Drainage coefficient 1
 Overall standard deviation 0.39
 PSI
 Load Transfer Coefficient
 Composite Modulus of Subgrade Reaction
 Loss of Support
 Effective Modulus of Subgrade Reaction
 Minimum thickness = 8’’

15. Joints
 Transverse Joint
 Joint spacing=21’
 18’’ long Dowels
 Longitudinal Joints
 Mandatory when width >18’

16. Pressure relief joint

17. Composite Pavement Design
 Designed as rigid pavement
 Concrete thickness obtained is reduced by an inch and
replaced by 3 inches of asphalt layer

18. Composite Pavement Design
 Designed as rigid pavement
 Concrete thickness obtained is reduced by an inch and
replaced by 3 inches of asphalt layer

19. Design of Flexible Pavement

20. Design of Flexible Pavement

21. Design of Flexible Pavement (contd.)
An example showing computation of Structural Number
Source: AASHTO 1993

22. Design of Flexible Pavement (contd.)
Once SN value is set, thickness design begins…
33322211 mDamDaDaSN
where a1, a2 and a3 are structural number coefficients obtained from
nomographs for MR values of materials used.
m2 and m3 are drainage coefficients obtained from table in design
manual..
The depth that results in a SN value close to the SN value obtained
from traffic loading, etc. is the design thickness. Thus , the design
solution is not unique.

23. Compulsory Aggregate Base Layer
Regardless of SN required, the aggregate base layer is
to be provided rather than asphalt –on –subgrade
buildup, particularly when full depth flexible design is
very thin.
Design of Flexible Pavement (contd.)
The aggregate base is less sensitive to moisture
than the subgrade and it separates the pavement
further from the subgrade.

24. Use of layer coefficients a1, a2 and a3
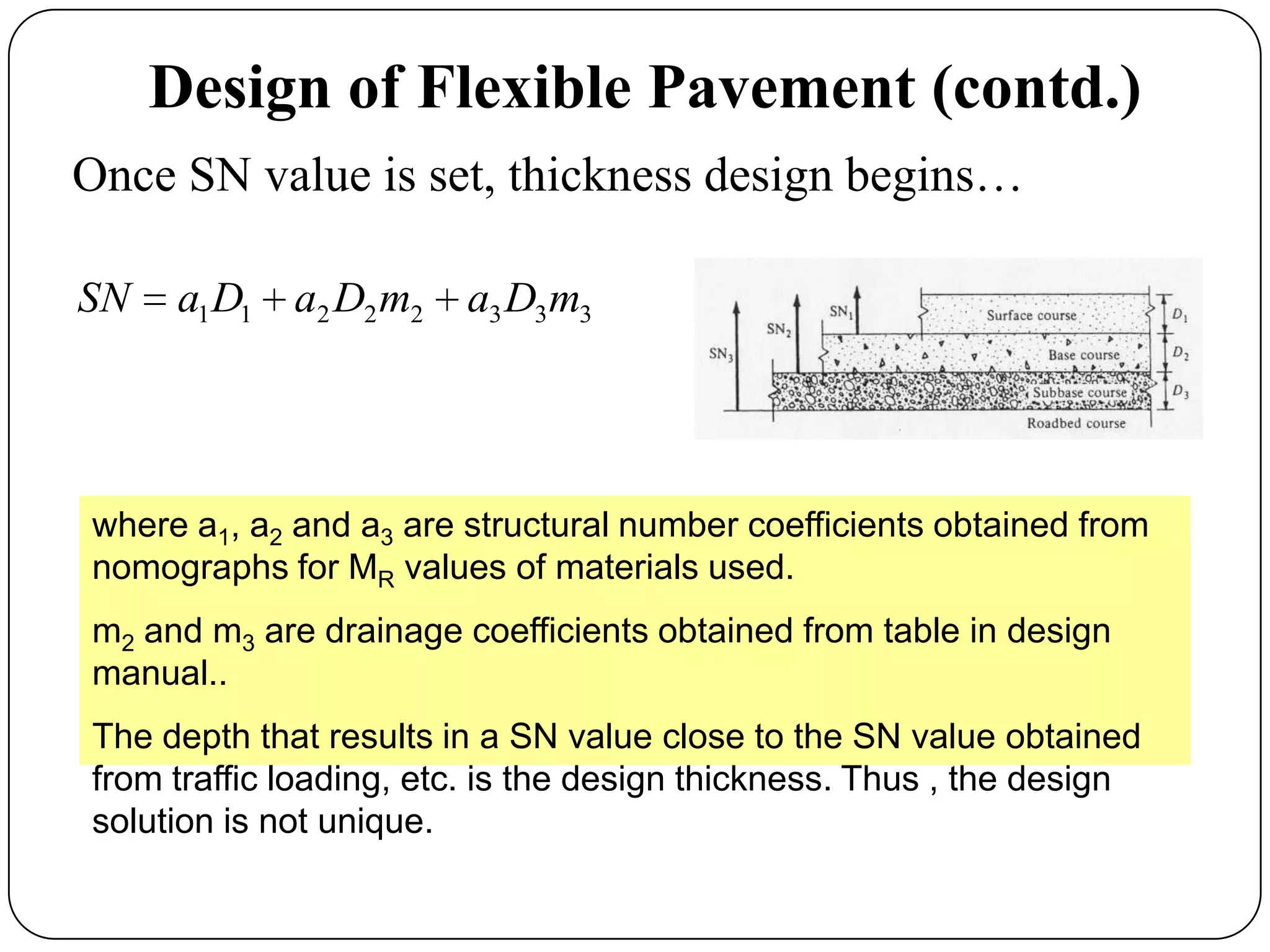
The approach of use of layer coefficients has been found
to be inappropriate for design purposes [Coree and
White (1990)]
The layer coefficient has been found to be NOT a simple
function of the individual layer modulus, but a function
of all layer thicknesses and properties. [Baladi and
Thomas (1994)]

25. Improvements in Flexible Pavement Design Equation
As per the present provisions, all distresses were lumped
to one composite index- PSI.
However, by predicting individual distresses and roughness
separately, a flexible pavement design process can be
optimized to meet the specific needs.
Generate separate designs for each of the individual
distresses and an optimum can be selected such that each
of the distresses can fall below a specific level.

26. References
 AASHTO. (1993). AASHTO Guide for Design of Pavements
Structures, American Association of State Highway and
Transportation Officials, Washington, DC
 Al Omari, Bashar and Daughter, M. I, (992). "Relationships
between IRI and PSR", Transportation engineering series no.69,
University of Illinois, Urbana.
 Baladi, G. Y., and A. Thomas. (1994). "Mechanistic Evaluation of
AASHTO Flexible Pavement Design Equations," Transportation
Research Record 1449, Washington, DC, pp. 72-78.
 Coree, B. J., and T. D. White. (1990). "AASHTO Flexible
Pavement Design Method: Fact or Fiction," Transportation
Research Record 1286, Washington, DC, pp. 206-216.
 HRB. (1962). "The AASHO Road Test. Report 7 - Summary
Report," Highway Research Board, National Academy of
Sciences - National Research Council, Washington, DC.
 "Pavement Design Manual", Ohio department of transportation,
Ohio, USA
 Schwartz, W.C. and Carvalho, L.R. (2007). "Evaluation of
Mechanistic-Empirical Design Procedure ", MDSHA project,
Maryland.
 Zhang, Z., J. P. Leidy, I. Kawa, and W. R. Hudson. (2000).
"Impact of Changing Traffic Characteristics and Environmental

27. Thank you all