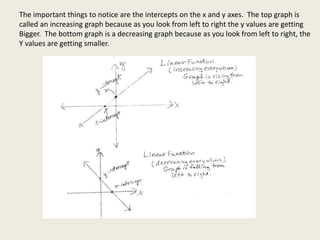
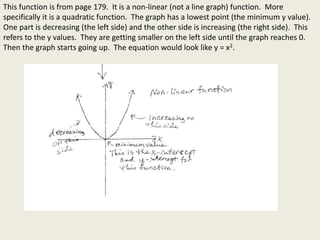
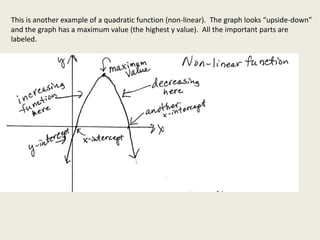
This document discusses features of linear, quadratic, and other non-linear functions. Linear functions have the form y=mx+b and are linear, while quadratic functions have the form y=ax^2+bx+c and have a minimum or maximum point. Other non-linear functions may have disconnected curves or sections that are increasing, decreasing, or constant. Key features to notice include intercepts and whether parts of the graph are increasing or decreasing based on the y-values from left to right.

1. Skill 34 Features of Linear and Quadratic Functions Use Pages 179, 180
in your book.
In this lesson, we will look at features of linear and quadratic functions and also
some functions that are just connected pieces.
Linear Functions and features These are the y = mx + b forms. The x is raised just
to the first power (no squares). See the next slide for a look at the features of the
Functions.
Quadratic Functions –These are the y =ax2+ b x + c type where there is a
squared term. These functions have either a minimum point or a maximum point.
Other “non-linear” functions have graphs that are just connected points or curves
that pass the vertical line test to be a function. They may also have maximum or
minimum points. They can have parts that are increasing or decreasing or
constant (not changing) when looking at the y values.

2. The important things to notice are the intercepts on the x and y axes. The top graph is
called an increasing graph because as you look from left to right the y values are getting
Bigger. The bottom graph is a decreasing graph because as you look from left to right, the
Y values are getting smaller.

3. This function is from page 179. It is a non-linear (not a line graph) function. More
specifically it is a quadratic function. The graph has a lowest point (the minimum y value).
One part is decreasing (the left side) and the other side is increasing (the right side). This
refers to the y values. They are getting smaller on the left side until the graph reaches 0.
Then the graph starts going up. The equation would look like y = x2.

4. This is another example of a quadratic function (non-linear). The graph looks “upside-down”
and the graph has a maximum value (the highest y value). All the important parts are
labeled.

5. This graph has an unusual shape. It has no special name—just “non-linear” because
it is not a line nor a curve. It still has a maximum point (highest y) and also a
Minimum (lowest y). Some parts are increasing from left to right, one part is
Decreasing, and one part is level (constant).