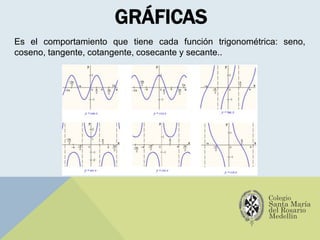
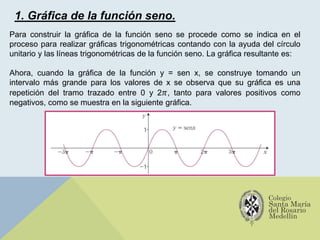
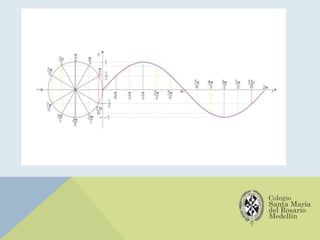
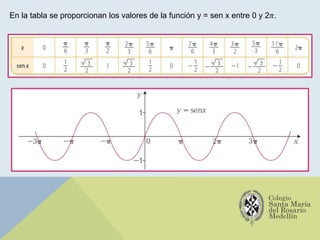
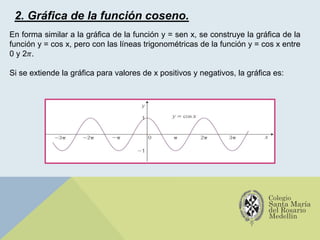
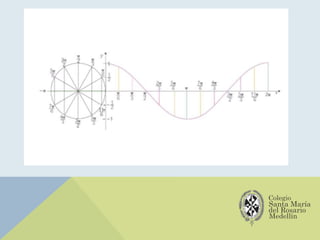
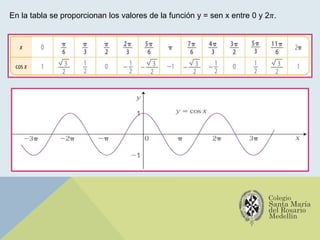
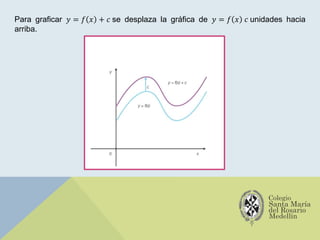
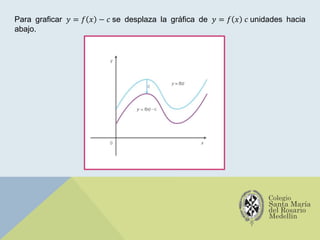
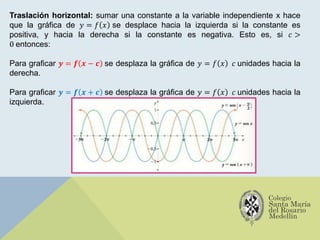
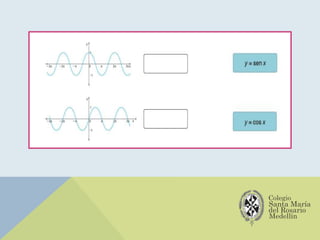
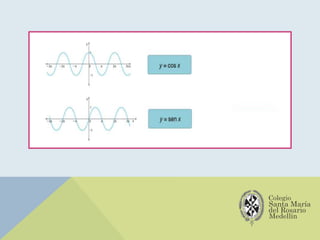
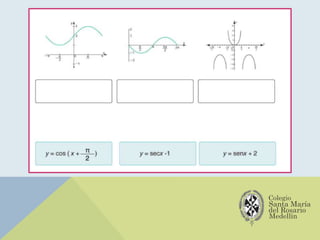
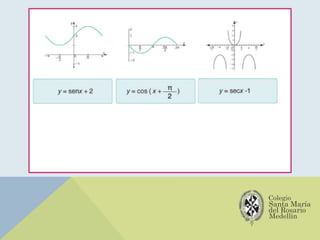
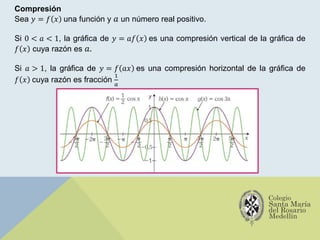
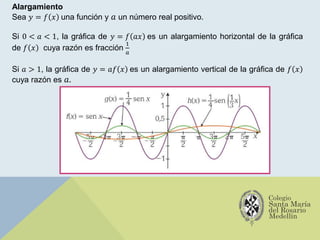
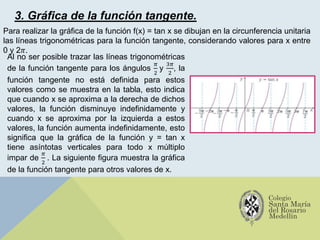
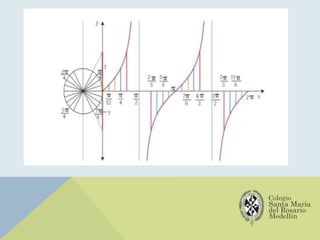
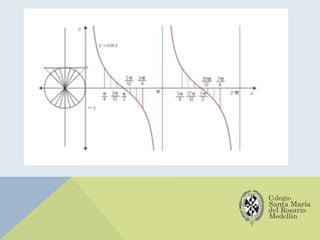
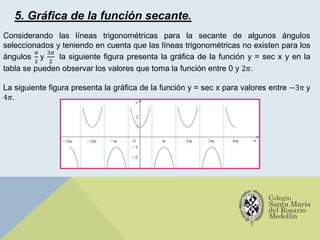
El documento analiza las gráficas de las funciones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante, describiendo sus características y métodos de construcción. Se explican transformaciones gráficas como traslaciones, reflexiones, compresiones y alargamientos que afectan el comportamiento de dichas funciones. También se incluyen ejemplos y recursos adicionales para profundizar en el estudio de gráficas trigonométricas.

2. GRÁFICAS
Es el comportamiento que tiene cada función trigonométrica: seno,
coseno, tangente, cotangente, cosecante y secante..

3. 1. Gráfica de la función seno.
Para construir la gráfica de la función seno se procede como se indica en el
proceso para realizar gráficas trigonométricas contando con la ayuda del círculo
unitario y las líneas trigonométricas de la función seno. La gráfica resultante es:
Ahora, cuando la gráfica de la función y = sen x, se construye tomando un
intervalo más grande para los valores de x se observa que su gráfica es una
repetición del tramo trazado entre 0 y 2𝜋, tanto para valores positivos como
negativos, como se muestra en la siguiente gráfica.

5. En la tabla se proporcionan los valores de la función y = sen x entre 0 y 2𝜋.

6. Características de la gráfica de la función seno.

7. 2. Gráfica de la función coseno.
En forma similar a la gráfica de la función y = sen x, se construye la gráfica de la
función y = cos x, pero con las líneas trigonométricas de la función y = cos x entre
0 y 2𝜋.
Si se extiende la gráfica para valores de x positivos y negativos, la gráfica es:

9. En la tabla se proporcionan los valores de la función y = sen x entre 0 y 2𝜋.

10. Características de la gráfica de la función coseno.

11. Análisis de Gráficas.
El análisis de gráficas es muy importante en la solución de problemas de
aplicación. Ciertas transformaciones de la función afectan la gráfica pero
permiten comprender mejor su comportamiento. La transformación puede ser
mediante traslación, reflexión, compresión y alargamiento.
Traslación
Considérese la gráfica de la función y = 𝑓(𝑥) La transformación de la función
mediante traslación puede ser vertical u horizontal.
Traslación vertical: sumar una constante a una función desplaza su gráfica
hacia arriba si la constante es positiva, y hacia abajo si la constante es negativa.
Esto es, si 𝑐 > 0 entonces:

12. Para graficar 𝑦 = 𝑓 𝑥 + 𝑐 se desplaza la gráfica de 𝑦 = 𝑓 𝑥 𝑐 unidades hacia
arriba.

13. Para graficar 𝑦 = 𝑓 𝑥 − 𝑐 se desplaza la gráfica de 𝑦 = 𝑓 𝑥 𝑐 unidades hacia
abajo.

14. Traslación horizontal: sumar una constante a la variable independiente x hace
que la gráfica de 𝑦 = 𝑓 𝑥 se desplace hacia la izquierda si la constante es
positiva, y hacia la derecha si la constante es negativa. Esto es, si 𝑐 >
0 entonces:
Para graficar 𝒚 = 𝒇 𝒙 − 𝒄 se desplaza la gráfica de 𝑦 = 𝑓 𝑥 𝑐 unidades hacia la
derecha.
Para graficar 𝒚 = 𝒇 𝒙 + 𝒄 se desplaza la gráfica de 𝑦 = 𝑓 𝑥 𝑐 unidades hacia la
izquierda.

16. Reflexión
Supóngase que se conoce la gráfica de 𝑦 = 𝑓 𝑥 , la reflexión de la función
puede ser respecto al eje x o respecto al eje y.
Reflexión respecto a y: para graficar la función 𝑦 = 𝑓 −𝑥 , se refleja la gráfica
de 𝑦 = 𝑓 𝑥 respecto al eje y.
Reflexión respecto a x: para graficar la función 𝑦 = −𝑓 𝑥 , se refleja la gráfica
de 𝑦 = 𝑓 𝑥 respecto al eje x.

21. Compresión
Sea 𝑦 = 𝑓 𝑥 una función y 𝑎 un número real positivo.
Si 0 < 𝑎 < 1, la gráfica de 𝑦 = 𝑎𝑓 𝑥 es una compresión vertical de la gráfica de
𝑓 𝑥 cuya razón es 𝑎.
Si 𝑎 > 1, la gráfica de 𝑦 = 𝑓 𝑎𝑥 es una compresión horizontal de la gráfica de
𝑓 𝑥 cuya razón es fracción
1
𝑎

22. Alargamiento
Sea 𝑦 = 𝑓 𝑥 una función y 𝑎 un número real positivo.
Si 0 < 𝑎 < 1, la gráfica de 𝑦 = 𝑓 𝑎𝑥 es un alargamiento horizontal de la gráfica
de 𝑓 𝑥 cuya razón es fracción
1
𝑎
Si 𝑎 > 1, la gráfica de 𝑦 = 𝑎𝑓 𝑥 es un alargamiento vertical de la gráfica de 𝑓 𝑥
cuya razón es 𝑎.

23. 3. Gráfica de la función tangente.
Para realizar la gráfica de la función f(x) = tan x se dibujan en la circunferencia unitaria
las líneas trigonométricas para la función tangente, considerando valores para x entre
0 y 2𝜋.
Al no ser posible trazar las líneas trigonométricas
de la función tangente para los ángulos
𝜋
2
y
3𝜋
2
, la
función tangente no está definida para estos
valores como se muestra en la tabla, esto indica
que cuando x se aproxima a la derecha de dichos
valores, la función disminuye indefinidamente y
cuando x se aproxima por la izquierda a estos
valores, la función aumenta indefinidamente, esto
significa que la gráfica de la función y = tan x
tiene asíntotas verticales para todo x múltiplo
impar de
𝜋
2
. La siguiente figura muestra la gráfica
de la función tangente para otros valores de x.

25. Características de la gráfica de la función tangente.

26. 4. Gráfica de la función cotangente.
La gráfica de la función cotangente se construye a partir de las líneas trigonométricas
correspondientes a la cotangente de cada uno de los ángulos seleccionados. En este
caso, los ángulos para los cuales no es posible obtener las líneas trigonométricas son
0, 𝜋 y 2𝜋 como se muestra en la tabla de valores y en la gráfica, entonces, se dice
que la función y = cot x no está definida para esos valores.
Además del método descrito anteriormente para
graficar la función y = cot x, se puede construir la
gráfica mediante la relacióncot 𝑥 =
1
tan 𝑥
, esto significa
que la función cotangente toma valores que son
inversos multiplicativos de la función tangente, por
tanto, la función cotangente es indefinida en los
valores en donde tan x = 0, esto es en los múltiplos de
normal pi, así que para estos valores la función y = cot
x tiene asíntotas verticales. La siguiente figura muestra
la gráfica de la función y = cot x para valores de x
entre −3𝜋 y 3𝜋 .

28. Características de la gráfica de la función cotangente.

29. 5. Gráfica de la función secante.
Considerando las líneas trigonométricas para la secante de algunos ángulos
seleccionados y teniendo en cuenta que las líneas trigonométricas no existen para los
ángulos
𝜋
2
y
3𝜋
2
la siguiente figura presenta la gráfica de la función y = sec x y en la
tabla se pueden observar los valores que toma la función entre 0 y 2𝜋.
La siguiente figura presenta la gráfica de la función y = sec x para valores entre −3𝜋 y
4𝜋.

31. Características de la gráfica de la función secante.

32. 6. Gráfica de la función cosecante.
La gráfica de la función y = csc x se construye a partir de las líneas trigonométricas
para valores de x entre 0 y 2𝜋 de la función cosecante. La figura muestra la gráfica de
la función y = csc x y en la tabla se muestran algunos valores de la función y = csc x.
Y la representación gráfica de la función para más valores se muestra en la siguiente
figura.

34. Características de la gráfica de la función cosecante.

38. LIBRO SANTILLANA
En el libro Santillana Vol. 2 pág. 106 a 110, 117, 118, 121y 122
podemos encontrar la definición y ejemplos de gráfica de
funciones trigonométricas.
En el libro Santillana Vol. 2 pág. 107, 108, 111, 115 y 123
podemos encontrar ejercicios de gráfica de funciones
trigonométricas.

39. Si quieren ver más ejercicios y ejemplos…
pueden visitar mi Instagram o pagina web, en
las cuales constantemente estaré publicando
contenido matemático.
https://www.instagram.com/joselprofe/
https://mathpage.wixsite.com/joselprofe

40. Pueden visitar los siguientes Links para ver más
ejemplos y explicación acerca de gráfica de
funciones trigonométricas.
https://www.youtube.com/watch?v=Dkdxks2ifBs
https://www.youtube.com/watch?v=VFSP4iNroQA
https://www.youtube.com/watch?v=fsvl1XBcXY0

41. ¡GRACIAS!