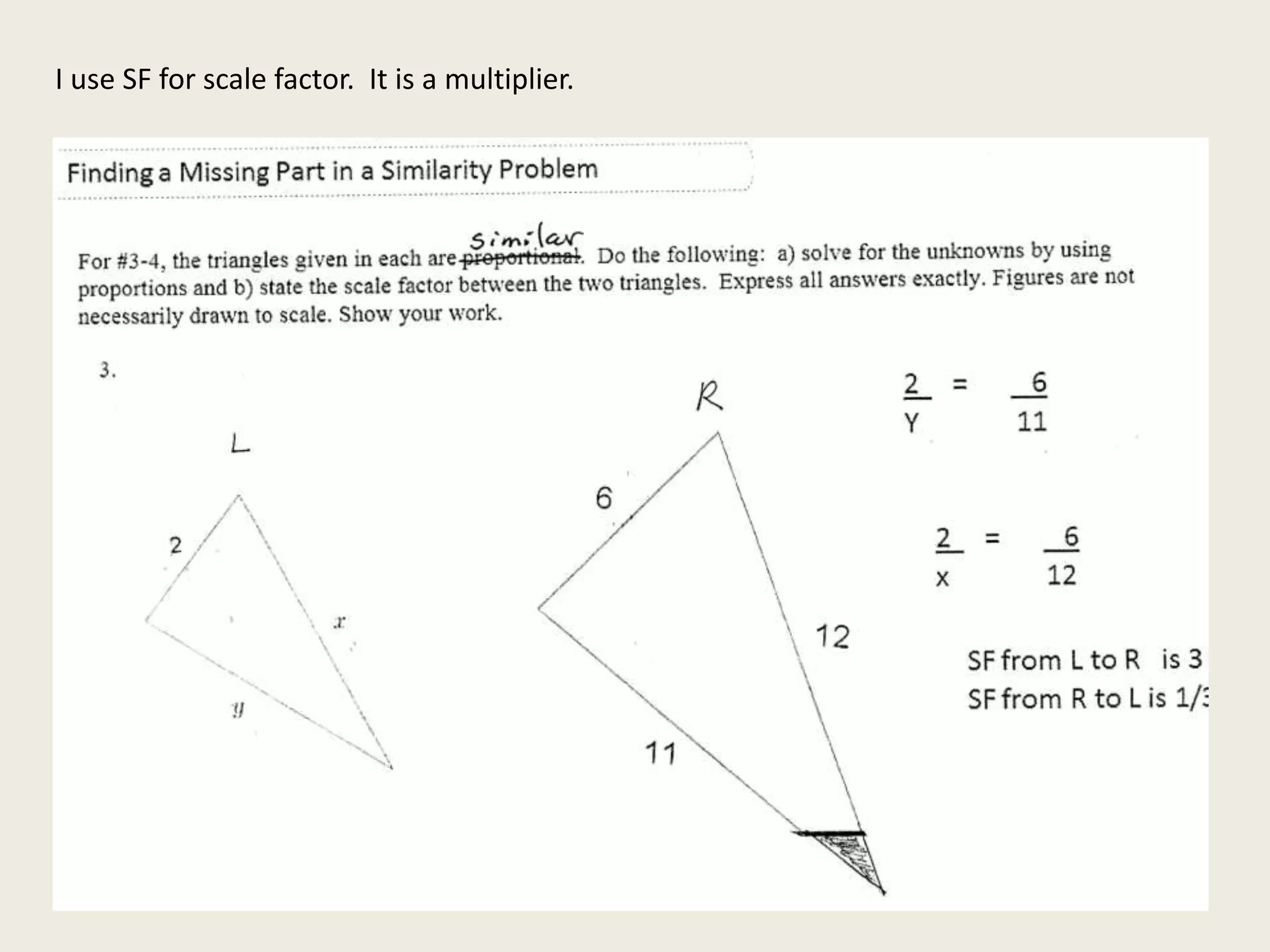
This document discusses using scale factors and proportions to solve scale drawing problems. Scale drawings are similar figures where the side lengths are related by a scale factor. To solve for a missing side length, a proportion is written using the corresponding sides and their scale factor relationship. Whether finding an actual length or a scale drawing length, proportions allow determining the missing part. Scale factors can be used to enlarge or shrink a figure and depend on the direction of scaling.

1. Skill 9 Scale Drawings and similar figures Pages 76-79 in the book
This lesson uses multipliers called scale factors to enlarge or shrink figures. These
figures are similar in that they have the same shape but different side lengths. The
side lengths which match up (corresponding) are related in a proportion.
We will be using the ideas of proportions to solve for missing sides. We studied these
ideas before.

2. To solve scale problems, write a proportion. Notice that I have put cm/km on both
sides of the proportion. There are other ways to do this, but this way is a good one.

3. This problem also uses a proportion to solve for the length on the drawing (not the actual
length). Whether you want the scale drawing length or the actual length, use a proportion
to solve for the missing part.

4. This slide
explains
how we can
just multiply
by the
scaled factor
to scale up a
similar
figure.

5. I use SF for scale factor. It is a multiplier.

6. Scale Factors depend on the direction of the scale. In this problem, you can go from
Figure A to Figure B so that the scale up factor is 12/8 or 1.5. That is all the sides of figure B are
1.5 times those of Figure A.
We can also scale down from Figure B to Figure A so that the scale factor is the reciprocal of
the other one 8/12 or 2/3. That is each side of Figure A is 2/3 times the corresponding side of
Figure B. On the test, you may only have to scale one way—not both ways.