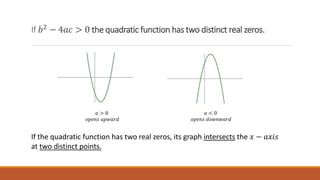
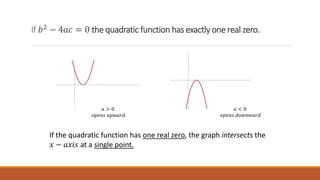
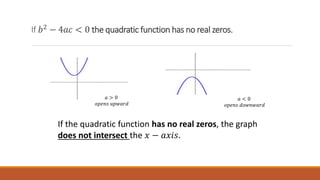
i. The document defines and explains the properties of constant, linear, quadratic, and piecewise functions through examples and formulas. ii. Constant functions have a horizontal line graph. Linear functions have a straight line graph described by the slope-intercept form y=mx+b. iii. Quadratic functions have a parabolic graph that opens up or down, with properties determined by the discriminant. Piecewise functions use different expressions over parts of the domain.

1. Examples of Functions
and Their Graphs
PRECALCULUS

2. 1. Constant Function
Definition 1.1 The function
𝑓 𝑥 = 𝑏
where 𝑏 is a real number is called the constant function.

3. 1.2 Properties of a Constant Function
i. The degree is 0.
ii. The domain of the constant function is the set of real numbers.
iii. The range is the set 𝑏 .
iv. The graph is a horizontal line whose 𝑦-intercept is 𝑏, and parallel to
the 𝑥 − 𝑎𝑥𝑖𝑠.

4. 2. Linear Functions
Definition 2. A function 𝑓 is a linear function if it can be written as
𝑓 𝑥 = 𝑚𝑥 + 𝑏
where 𝑚 and 𝑏 are real numbers, 𝑚 ≠ 0.

5. i. A linear function is a first-degree function.
ii. The domain of 𝑓 is the set of real numbers.
iii. The range of 𝑓 is the set of real numbers.
iv. The graph of a linear function is a straight line with slope 𝑚 and
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡 𝑏. It is a slanting straight line.
v. A linear function is increasing if 𝑚 > 0 and decreasing if 𝑚 < 0.
vi. A linear function has exactly one zero, occurring at 𝑥 = −
𝑏
𝑚
.
2.1 Properties of Linear Functions

6. Remarks: Zeros of a Function
1) The zeros of a function 𝑓 are the values of 𝑥 for
which 𝑓(𝑥) = 0.
2) A real zero of a function is also an 𝑥 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡 of
the graph of the function.

7. 2.2 Equations of a Straight Line: A Review
I. The General Equation of a Line
The equation of a line can be written to the general form or to the
standard form
𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0
where 𝐴, 𝐵 and 𝐶 are real numbers, and 𝐴 𝑎𝑛𝑑 𝐵 𝑎𝑟𝑒 𝑛𝑜𝑡 𝑏𝑜𝑡ℎ 𝑧𝑒𝑟𝑜.

8. 2.3 The Slope of a Line: A Review
Definition 2.3.1 Consider a line that is not parallel to the 𝑦 − 𝑎𝑥𝑖𝑠.
Let 𝑃1 𝑥1, 𝑦1 and 𝑃2 𝑥2, 𝑦2 be two distinct points on the line.
The slope 𝑚 of the line is given by
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1
where 𝑥1 ≠ 𝑥2

9. Remarks:
1) The value of 𝑠𝑙𝑜𝑝𝑒 𝑚 is the same number no matter what two points on line
are selected.
2) A line with a positive slope 𝑚 > 0 goes up (or rises) from left to right, while
a line with a negative slope 𝑚 < 0 goes down (or falls) from left to right.
3) A horizontal line has zero slope 𝑚 = 0 .
4) A vertical line has undefined slope.

10. 1. Point-Slope Form
𝒚 − 𝒚𝟏 = 𝒎 𝒙 − 𝒙𝟏
2. Slope-Intercept Form
𝒚 = 𝒎𝒙 + 𝒃 𝒔𝒍𝒐𝒑𝒆 𝒎 𝒂𝒏𝒅 𝒚 − 𝒊𝒏𝒕𝒆𝒓𝒄𝒆𝒑𝒕 𝒃
𝒚 = 𝒎 𝒙 − 𝒂 𝒔𝒍𝒐𝒑𝒆 𝒎 𝒂𝒏𝒅 𝒙 − 𝒊𝒏𝒕𝒆𝒓𝒄𝒆𝒑𝒕 𝒂
3. Two-Point Form
𝒚 − 𝒚𝟏 =
𝒚𝟐 − 𝒚𝟏
𝒙𝟐 − 𝒙𝟏
𝒙 − 𝒙𝟏
4. Intercepts Form
𝒙
𝒂
+
𝒚
𝒃
= 𝟏
2.2 Equations of a Straight Line: A Review

11. Parallel and Perpendicular Lines
Theorem 1 Parallel Lines. Let 𝐿1 and 𝐿2 be two
distinct non-vertical lines with slopes 𝑚1and 𝑚2,
respectively. Then 𝐿1 is parallel to 𝐿2 if and only if
𝑚1 = 𝑚2.
𝐿2

12. Parallel and Perpendicular Lines
Theorem 2 Perpendicular Lines. Let 𝐿1 and 𝐿2 be two
distinct non-vertical lines with slopes 𝑚1and 𝑚2,
respectively. Then 𝐿1 is perpendicular to 𝐿2 if and
only if 𝑚1𝑚2 = −1.

13. 3. Quadratic Function
Definition 3. The quadratic function is defined by
𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐
where 𝑎, 𝑏 and 𝑐 are real numbers, 𝑎 ≠ 0.

14. 1) The domain of any quadratic function is the set of real numbers.
2) The graph is a parabola with vertex at
−𝑏
2𝑎
,
4𝑎𝑐−𝑏2
4𝑎
and whose axis is vertical.
Properties of a Quadratic Function

15. 3) The zeros of the quadratic function 𝑓 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 coincide
with the roots of the equation 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0. These roots are
given by the quadratic formula
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
Properties of a Quadratic Function

16. 4) The expression 𝑏2
− 4𝑎𝑐 in the quadratic formula is called the discriminant
of the quadratic function because its value tells us whether the function has
real zeros, and how many zeros to expect.
 if 𝑏2
− 4𝑎𝑐 > 0 the quadratic function has two distinct real zeros.
if 𝑏2 − 4𝑎𝑐 = 0 the quadratic function has exactly one real zero.
if 𝑏2 − 4𝑎𝑐 < 0 the quadratic function has no real zeros.
Properties of a Quadratic Function

17. If 𝑏2
− 4𝑎𝑐 > 0 the quadratic function has two distinct real zeros.
If the quadratic function has two real zeros, its graph intersects the 𝑥 − 𝑎𝑥𝑖𝑠
at two distinct points.
𝑎 > 0
𝑜𝑝𝑒𝑛𝑠 𝑢𝑝𝑤𝑎𝑟𝑑
𝑎 < 0
𝑜𝑝𝑒𝑛𝑠 𝑑𝑜𝑤𝑛𝑤𝑎𝑟𝑑

18. If 𝑏2
− 4𝑎𝑐 = 0 the quadratic function has exactly one real zero.
If the quadratic function has one real zero, the graph intersects the
𝑥 − 𝑎𝑥𝑖𝑠 at a single point.
𝑎 > 0
𝑜𝑝𝑒𝑛𝑠 𝑢𝑝𝑤𝑎𝑟𝑑
𝑎 < 0
𝑜𝑝𝑒𝑛𝑠 𝑑𝑜𝑤𝑛𝑤𝑎𝑟𝑑

19. If 𝑏2
− 4𝑎𝑐 < 0 the quadratic function has no real zeros.
𝑎 > 0
𝑜𝑝𝑒𝑛𝑠 𝑢𝑝𝑤𝑎𝑟𝑑
𝑎 < 0
𝑜𝑝𝑒𝑛𝑠 𝑑𝑜𝑤𝑛𝑤𝑎𝑟𝑑
If the quadratic function has no real zeros, the graph
does not intersect the 𝑥 − 𝑎𝑥𝑖𝑠.

20. 5) When the graph of a quadratic function opens upward 𝑎 > 0 , the function
has a minimum value, which occurs at the vertex of the parabola. In this
case, the range of the function is
𝑦 𝑦 ≥
4𝑎𝑐 − 𝑏2
4𝑎
𝑜𝑟
4𝑎𝑐 − 𝑏2
4𝑎
, +∞
Properties of a Quadratic Function

21. 6) When the graph of a quadratic function opens downward 𝑎 < 0 , the
function has a maximum value, which occurs at the vertex of the parabola.
In this case, the range of the function is
𝑦 𝑦 ≤
4𝑎𝑐 − 𝑏2
4𝑎
𝑜𝑟 −∞,
4𝑎𝑐 − 𝑏2
4𝑎
Properties of a Quadratic Function

22. 4.0 Split or Piecewise-Defined Function
Definition 4.1 A split or piecewise-defined function is a
function that is defined by using several expressions for
different parts of the domain.