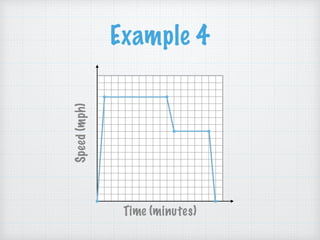
This document discusses sketching graphs and functions using key features. It provides 4 examples of functions with given features and asks the reader to sketch the graph based on those features. Example 1 is a linear function that is positive for x>1 and increasing for all x. Example 2 is also linear, with a y-intercept of 1, being continuous and positive between -1 and 3, and having a maximum at (1,2) while increasing for x<1. Example 3 is nonlinear and continuous about x=1, with a minimum at (1,0) and approaching infinity as x approaches positive and negative infinity. Example 4 models a bike ride, asking the reader to sketch a graph based on features like the y-

1. Section 2-4
Sketching Graphs and Functions

2. Essential Questions
• How do you use the key features of functions to
sketch graphs of linear functions?
• How do you use the key features of functions to
sketch graphs of nonlinear functions?

3. Example 1
As x → +∞, f (x ) → +∞, and as x → −∞, f (x ) → −∞.
Use the given key features to sketch a linear graph.
The y-intercept is (0, 2). The function is positive for
x>1. The function is increasing for all values of x.
x
y

4. Example 2
As x → +∞, f (x ) → −∞,
and as x → −∞, f (x ) → −∞.
Use the given key features to sketch a linear graph.
The y-intercept is (0, 1). The function is continuous.
The functions in positive for -1<x<3. The function has
a maximum at (1,2). The function is increasing for x<1.
x
y

5. Example 3
As x → +∞, f (x ) → +∞,
and as x → −∞, f (x ) → +∞.
Use the given key features to sketch a linear graph.
The function is nonlinear and not made of segments.
The function is continuous about the line x=1. The
function has a minimum at (1,0).
x
y

6. Example 4
Use the given key features to sketch a graph. Maggie
Brann goes for a bike ride on a bike path near her house.
y-intercept: Maggie starts at 0 mph.
Linear or nonlinear: The function that models the situation
is nonlinear.
Extrema: Maggie’s maximum speed is 15 mph, which she
reaches 1 minute after starting her bike ride.
Increasing: Maggie’s speed increases steadily for the first
minute.
Decreasing: At the 10-minute mark, Maggie decreases her
speed for 1 minute, then she stays at 10 mph for 5
minutes. At the 16-minute mark, she again decreases her
speed for 1 minute until she reaches a stop.

7. Example 4
Time (minutes)
Speed(mph)