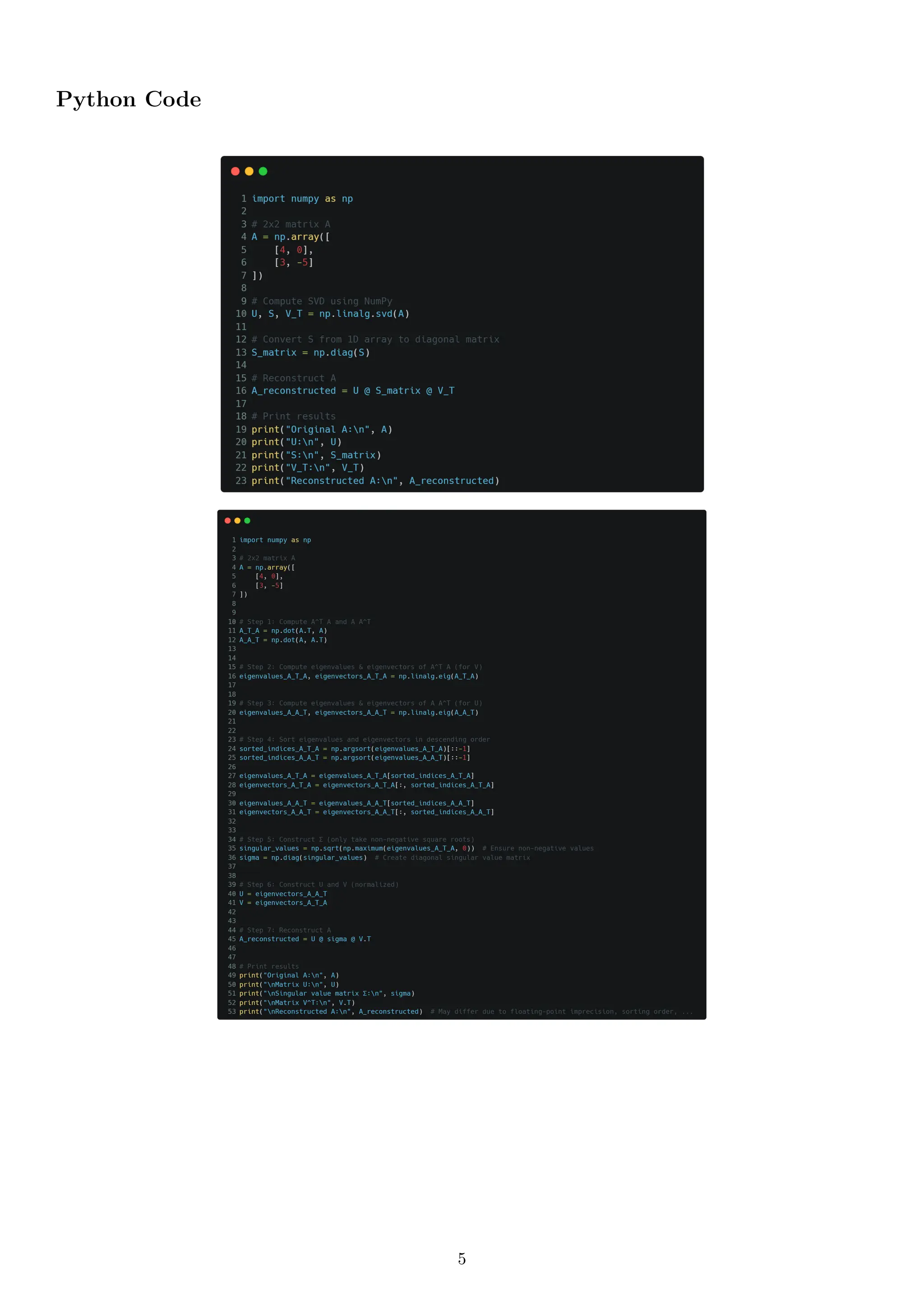
SVD is a powerful matrix factorization technique used in machine learning, data science, and AI. It helps with dimensionality reduction, image compression, noise filtering, and more. Mastering SVD can give you an edge in handling complex data efficiently!

1. Singular Value Decomposition (SVD)
Mohamed Gamal
Introduction
Singular Value Decomposition (SVD) is a fundamental matrix factorization technique used in machine learn-
ing, data science, and numerical computing, it is a generalization of the eigendecomposition that works for
any matrix (square or rectangular). Unlike eigendecomposition, which applies only to square matrices, SVD
decomposes a matrix into three separate matrices
A = UΣVT
where
ˆ U is an orthogonal (or unitary) matrix (columns are orthonormal eigenvectors of AAT ).
ˆ Σ is a diagonal matrix with singular values (square roots of the eigenvalues of AT A).
ˆ V T is an orthogonal (or unitary) matrix (rows are orthonormal eigenvectors of AT A)
This decomposition has several properties that make it more stable and powerful than other decompositions
like LU, QR, or eigendecomposition.
Why is SVD Important?
SVD has many applications, including:
ˆ Dimensionality Reduction (e.g., Principal Component Analysis)
ˆ Image Compression
ˆ Noise Reduction
ˆ Pseudoinverse Calculation
ˆ etc.
It provides a stable and robust way to analyze and manipulate data, making it essential in machine learning
and optimization.
1

2. Example
Let’s consider the 2x2 matrix
A =
4 0
3 −5
Step 1: Compute AT
A and AAT
First, we compute AT A
AT
A =
4 3
0 −5
4 0
3 −5
=
25 −15
−15 25
(1)
Now, compute AAT
AAT
=
4 0
3 −5
4 3
0 −5
=
16 12
12 34
(2)
Step 2: Compute Eigenvalues of AT
A
The characteristic equation is given by
det(AT
A − λI) = 0
25 − λ −15
−15 25 − λ
= 0
Expanding the determinant
(25 − λ)(25 − λ) − (−15)(−15) = 0
(25 − λ)2
− 225 = 0
(25 − λ)2
= 225
Solving for λ
λ1 = 40, λ2 = 10
Singular values are the square roots
σ1 =
√
40 ≈ 6.32, σ2 =
√
10 ≈ 3.16
Thus, the singular value matrix is
Σ =
σ1 0
0 σ2
=
6.32 0
0 3.16
(3)
Step 3: Compute Eigenvectors of AT
A for V
AT
A − λI
v = 0
For λ1 = 40:
−15 −15
−15 −15
v1
v2
= 0
−15v1 − 15v2 = 0
v2 = −v1
Setting v1 = 1 and normalizing, we get
v =
1
√
2
1
−1
2

3. For λ2 = 10:
15 −15
−15 15
v1
v2
= 0
15v1 − 15v2 = 0
v1 = v2
Setting v1 = 1 and normalizing, we get
v =
1
√
2
1
1
Therefore, the Right Singular Vectors matrix V is
V =
1
√
2
1 1
−1 1
(4)
Step 4: Compute Eigenvectors of AAT
for U
We solve the characteristic equation for AAT
det(AAT
− λI) = 0
16 − λ 12
12 34 − λ
= 0
Expanding
(16 − λ)(34 − λ) − (12)(12) = 0
λ2
− 50λ + 400 − 144 = 0
λ2
− 50λ + 256 = 0
Solving for λ
λ1 = 40, λ2 = 10
Eigenvectors for λ1 = 40:
−24 12
12 −6
u1
u2
= 0
−24u1 + 12u2 = 0
2u1 = u2
Setting u2 = 1 and normalizing, we get
u =
1
√
5
2
1/2
1
=
1
√
5
1
2
For λ2 = 10:
6 12
12 24
u1
u2
= 0
6u1 + 12u2 = 0
u1 = −2u2
Setting u2 = 1 and normalizing, we get
u =
1
√
5
−2
1
Therefore, the Left Singular Vectors matrix U is
U =
1
√
5
1 −2
2 1
=
0.45 −0.89
0.89 0.45
(5)
3

4. Final SVD Decomposition
Thus, using equations (3), (4), and (5) we have
A = UΣVT
where
U =
0.45 −0.89
0.89 0.45
,
Σ =
6.32 0
0 3.16
,
VT
=
1
√
2
1 1
−1 1
T
=
1
√
2
1 −1
1 1
4

5. Python Code
5