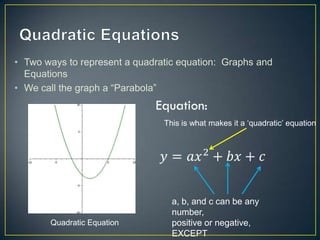
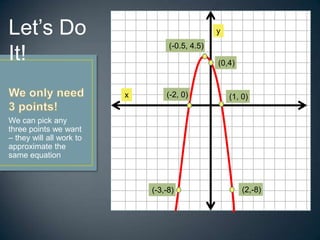
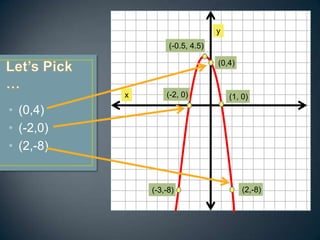
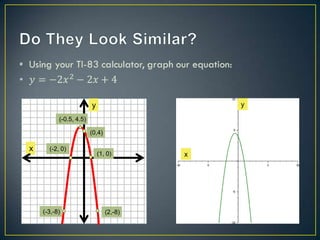
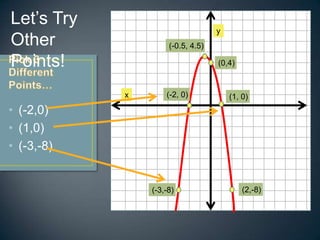
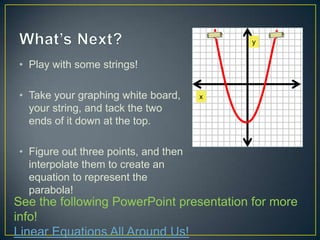
This document provides an ASSURE model for a math lesson on graphing and interpolating quadratic equations for a high school Algebra 2 class. The lesson objectives are for students to correctly substitute points on a graph into a quadratic function 80% of the time and graph quadratic equations on a graphing calculator choosing an appropriate window 80% of the time. The lesson involves representing quadratic equations as graphs and equations, identifying key features of parabolas, using three points to find the equation of a graph, and practicing with different point sets.

1. Devon Kinne
CIMT 543 – Summer 2012

2. ASSURE MODEL
Target Learners High School - Algebra 2 class
Subject Area Math: Interpolating and Graphing
Quadratic Equations
Learning Objectives: Students will substitute points on a
graph into a function form to find the
equation of a graph correctly 80% of
the time.
Students will graph quadratic
equations on their graphing
calculator, choosing an appropriate
window to view the graph, 80% of the
time.

3. • Two ways to represent a quadratic equation: Graphs and
Equations
• We call the graph a “Parabola”
This is what makes it a „quadratic‟ equation
a, b, and c can be any
number,
Quadratic Equation positive or negative,
EXCEPT

4. •
Degree = 2, so I need at least 3
points

5. Let‟s Do y
(-0.5, 4.5)
It! (0,4)
x (-2, 0) (1, 0)
We can pick any
three points we want
– they will all work to
approximate the
same equation
(-3,-8) (2,-8)

6. y
(-0.5, 4.5)
(0,4)
x (-2, 0) (1, 0)
• (0,4)
• (-2,0)
• (2,-8)
(-3,-8) (2,-8)

7. •
4=c
0 = 4a – 2b + c
-8 = 4a + 2b + c

8. • Goal: Solve the system of equations by the addition
method
• Addition Method: Add like terms of each equation
• Example: 2x + y = 9 2x + y = 9
+ 3x – y = 16 + 3x - y = 16
• 2x + y = 9
5x +0y= 25
3x – y = 16
5x = 25 x=5
• Now, substitute x=5 into either equation
2(5) + y = 9 10 + y = 9 y = -1
We have our solution! (x,y) = (5, -1)

9. • What happens if we just can‟t add down?
• Example:
2x + y = 9 2x + y = 9
2x + y = 9
+ 3x + y = 4 + 3x + y = 4
3x + y = 4 5x +2y= 13
We still
have an x
AND a y!
• We can multiply an entire row in order to create a
cancellation
-2x - y = -9
(-1)* (2x + y = 9) -2x - y = -9
+ 3x +y = 4
+ 3x + y = 4 + 3x +y = 4
1x +0y= -5
• So, x= - 5. Substitute x=-5 into either equation
2(-5) + y = 9 -10 + y = 9 y = 19
We have our solution! (x,y) = (-5, 19)

10. x+y=5
-x + y = 3
(x,y) = (1,4)
4x + 5y = -2
3x + y = 4 (x,y) = (2,-2)
2x - y = 9
3x +4y = -14 (x,y) = (2,-5)
4x - 3y = 25
-3x + 8y = 10
(x,y) = (10,5)

11. • 3 equations with 3 unknowns 4 = 0a + 0b + c
0 = 4a - 2b + c
-8 = 4a + 2b + c
• We do the same process, but it will take more steps
because we have 3 unknowns!
But Wait! Above, we see 4 = c . We can
make that substitution, and then only have 2
equations and 2 unknowns!

12. 4=c Subtract -4 = 4a - 2b
Substitut 0 = 4a - 2b + 4
0 = 4a - 2b + c 4 from -12 = 4a + 2b
e c=4 -8 = 4a + 2b + 4 each side
-8 = 4a +2b + c
-4 = 4a - 2b Solve
-4 = 4a - 2b Add
+ -12 = 4a +2b a = -2
-12 = 4a +2b rows for a
-16 = 8a + 0
• Now, substitute a=-2 into either equation
-4 = 4(-2) - 2b -4 = -8 - 2b b = -2
We have our solution! (a,b,c) = (-2,-2, 4)

13. •
y y
(-0.5, 4.5)
(0,4)
x (-2, 0)
(1, 0) x
(-3,-8) (2,-8)

14. Let‟s Try
y
Other (-0.5, 4.5)
Points! (0,4)
x (-2, 0) (1, 0)
• (-2,0)
• (1,0)
• (-3,-8)
(-3,-8) (2,-8)

15. • 3 equations with 3 unknowns 0 = 4a - 2b + c
0 = 1a +1b + c
-8 = 9a - 3b + c
• We do the same process, but it will take more steps
because we have 3 unknowns!
Wait! We don‟t have an easy substitution
like before, where c=4. But we still need to
do the same thing – get an equation that
looks like:
c = something!

16. • Goal: Isolate “c” in one of the equations, to give us 2
remaining equations with 2 unknowns (a and b)
0 = 4a - 2b + c We can choose any of
0 = 1a +1b + c these equations, since
they all have “c” with no
-8 = 9a - 3b + c coefficient, it‟s easy to
solve for “c”
• Now, solve 0 = 4a – 2b + c for “c”
4a -2b + c = 0 Subtract -2b + c = -4a
4a from
Add 2b to
each side c = 2b-4a
each side
We can now sub “c” into the other two equations

17. c = 2b-4a
Substitute 0 = -3a + 3b
0 = 1a +1b + c for c=2b-
0 = 1a + 1b + 2b-4a simplif
-8 = 9a - 3b + 2b-4a y -8 = 5a - 1b
-8 = 9a - 3b + c 4a
Multiply 0 = -3a + 3b Add 0 = -3a + 3b
0 = -3a + 3b
2nd row by
-24= 15a - 3b + -24 = 15a - 3b
-8 = 5a - 1b rows
3 -24 = 12a + 0
Solve
-24 = 12 a -2 = a
for a

18. c = 2b-4a
Original equations: 0 = 1a +1b + c Simplified 0 = -3a + 3b
-8 = 9a - 3b + c to -8 = 5a - 1b
• Now, substitute a=-2 into either simplified equation
0= -3(-2) + 3b 0 = 6 + 3b b = -2 a = -2
• Now, substitute a=-2, b=-2 into our “c”equation
c= 2(-2) -4(-2) c = -4 + 8 b = -2 a = -2
c=4
We have our solution! (a,b,c) = (-2,-2, 4)
Hooray! It‟s the same as
before!

19. y
• Play with some strings!
• Take your graphing white board, x
your string, and tack the two
ends of it down at the top.
• Figure out three points, and then
interpolate them to create an
equation to represent the
parabola!
See the following PowerPoint presentation for more
info!
Linear Equations All Around Us!

20. • Clipart taken from Microsoft PowerPoint Clipart Library
• Images designed by Devon Kinne
Kinne, D. (2012). Linear equations all around us -
powerpoint presentation. Retrieved June 10, 2012 from
https://www.dropbox.com/s/ohpjydb9zwfp83n/LinearEq
uationPresentation.wmv
Kinne, D. (2012). Parabolas all around us webquest.
Retrieved June 10, 2012, from
http://parabolasaroundus.weebly.com/
Smaldino, S.E., Lowther, D.L., & Russell, J.D. (2012).
Instructional technology and media for learning (10th
ed.). Boston, MA: Pearson Education, Inc.