Il sillogismo è un tipo di ragionamento logico composto da due premesse e una conclusione, utilizzando un termine medio. Si distingue in tre tipi: categorico, ipotetico e disgiuntivo, con rigide regole per determinare la validità. La validità si basa su forme formali, non sulla verità delle affermazioni, e ci sono 256 forme di sillogismi teoricamente, di cui solo 19 sono considerati validi.

1. Cos' è il sillogismo ?

da syn, "insieme", e logismòs, "calcolo" :
ragionamento concatenato.

Tutti gli uomini (M) sono mortali (A)

Socrate (B) è un uomo (M)

Socrate (B) è mortale (A)
Diagramma
di Eulero-Venn

2. Termine medio

Il termine medio è la chiave del sillogismo:
(PM) Tutti gli uomini sono mortali
(pm) Socrate è un uomo termine medio: uomo
(C) Dunque Socrate è mortale

Come si riconosce? è quello ripetuto in PM e pm

M è la chiave perchè
è contenuto in A
e contiene B
Diagramma
di Eulero-Venn

3. 3 Tipi di sillogismo

Tre tipi di Sillogismo: categorico (il più noto), ipotetico e disgiuntivo.
1. Categorico: le affermazioni sono categoriche, assolute, non
condizionate, si esclude il dubbio.
2. Ipotetico: la Premessa maggiore è un'ipotesi
3. Disgiuntivo: la premessa maggiore è una disgiunzione

4. 1. Sillogismo Categorico
Le affermazioni sono categoriche, assolute, non condizionate, si esclude il
dubbio
(PM) Tutti gli uomini sono mortali (pm) Tutti i greci sono uomini
→ (C) Dunque tutti i greci sono mortali
(PM) Ogni animale è mortale (pm) Ogni uomo è animale
→ (C) Dunque ogni uomo è mortale
(PM)Tutte le trote sono pesci (pm) Qualche animale non è un pesce
→ ( C) Qualche animale non è una trota

5. 2. Sillogismo Ipotetico
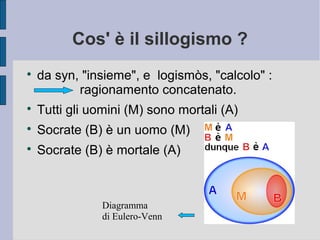
Il sillogismo ipotetico si fonda su un'ipotesi:
Se piove (p) prendo l'ombrello (q) Non prendo l'ombrello (¬ q)
→ Quindi non piove (¬ p)
[(p → q) (¬ q)] → (¬ p)∧ in linguaggio formale, dove '→' significa
derivazione, conseguenza logica (implicazione materiale) e '¬' è il segno
della negazione.
L'ipotesi è p

6. 3. Sillogismo disgiuntivo
ll sillogismo disgiuntivo è una regola d'inferenza che ha come PM una
disgiunzione (inclusiva od esclusiva)dunque, se un termine è falso, l'altro
è sicuramente vero.
Esempio
Oggi vado a spasso o studio.(p V q)
Ma non studio.(¬q)
Dunque, oggi vado a spasso.(p )

7. Le forme delle proposizioni

Le proposizioni che compongono un sillogismo categorico
possono essere di forma diversa:

universali affermative ("Tutti gli S sono P") A

particolari affermative ("Qualche S è P"), I

universali negative ("Nessun S è P"), E

particolari negative ("Qualche S non è P"). O

Come si vede, ad ogni forma corrisponde una lettere, la prima e
la seconda vocale dei verbi latini affirmo e nego

8. Universali affermative (A)

1. Universale affermativa: “tutti gli S sono P”

L’enunciato afferma che ogni elemento che ha la proprietà S ha anche
la proprietà P. Es. Tutti i greci sono europei.

Dandone una rappresentazione grafica, col diagramma di Eulero-Venn:
S
P
In logica dei predicati:
∀x∈ S | x∈ P
In teoria degli insiemi: S P

9. Particolari affermative (I)

2. Particolare affermativa: “qualche S è P”

L’enunciato afferma che solo qualche elemento che ha la proprietà S ha
anche la proprietà P. Es: Qualche greco è calvo

Dandone una rappresentazione grafica, col diagramma di Eulero-Venn:
In logica dei predicati:
∃x A| x B∈ ∈
A B
In teoria degli insiemi:

10. Universali negative (E)

3. Universale negativa: “nessun S è P”

L’enunciato afferma che nessun elemento che ha la proprietà S ha la
proprietà P. Es. Nessun greco è polacco

Dandone una rappresentazione grafica, col diagramma di Eulero-Venn:
S P In logica dei predicati:
∀x S | x P∈
In teoria degli insiemi: P Q =

11. Particolari Negative (O)
4. Particolare negativa: “qualche S non è P”
L’enunciato afferma che qualche elemento che ha la proprietà S non ha la
proprietà P. Es.Qualche greco non è giovane.
In logica dei predicati:
In teoria degli insiemi: P – Q
∃ x S∈ | x P

12. Le proposizioni del sillogismo
Forma Esempio Teoria degli insiemi Logica dei predicati
Universale
affermativa A
Tutti gli S sono P S P
∀x∈ S | x∈ P
I Particolare
Affermativa I
Alcuni S sono P S P ∃x S| x P∈ ∈
E Universale
Negativa E
Nessun S è P P S = ∀x S | x P∈
O Particolare
Negativa O
Alcuni S non sono P S - P
∃ x S | x∈ P
Tav. 1

13. I termini del sillogismo: S, M e P
(PM) Tutti gli uomini sono mortali predicato (P) : mortale
(pm) Socrate è un uomo termine medio (M): uomo
(C) Dunque Socrate è mortale Soggetto (S): Socrate
Le due premesse hanno sempre un termine in comune e la conclusione
lega sempre il soggetto della premessa minore (la seconda) al predicato
della premessa maggiore (la prima)

14. Definizione
Unn sillogismo è una inferenza costituita da due premesse e una
conclusione le quali sono tutte e tre proposizioni di uno dei quattro tipi
evidenziati in precedenza ( A I E O) .
Le due premesse devono avere una proprietà comune,
il termine medio (M) e nella conclusione figurano, nell’ordine, le altre due
proprietà presenti nella premessa minore, il Soggetto (S) e nella
premessa maggiore, il predicato (P).

15. Figure e modi del sillogismo
I sillogismi categorici si caratterizzano in base a due aspetti : le figure e i
modi.
Le differenti disposizioni dei termini di un sillogismo danno luogo alle
diverse figure di sillogismo
Le differenti combinazioni delle forme delle proposizioni di un sillogismo
danno luogo ai modi del sillogismo

16. Figure
FIGURA
I
FIGURA
II
FIGURA
III
FIGURA
IV
Premessa
Maggiore
MP PM MP PM
Premessa
Minore
SM SM MS MS
I termini che abbiamo definito possono essere disposti in modo diverso
nelle premesse e in base a ciò si distinguono le figure di un sillogismo.
Aristotele ne individuò tre, i medievali ne aggiunsero una quarta
Tav. 2

17. I Modi
Si dice modo di un sillogismo la successione (nell’ordine) dei tre tipi di
enunciati che lo compongono (premessa maggiore, premessa minore e
conclusione). Ad esempio il seguente sillogismo ha modo EIO:
 Nessun gorilla è un gatto (Universale Negativa) E
 Qualche scimmia è un gorilla ( Particolare Affermativa) I
 Qualche scimmia non è un gatto ( Particolare Negativa) O
Ed è una prima figura vista la posizione del termine medio “gorilla “ del
soggetto scimmia e del predicato gatto : MP-SM

18. Esempio di classificazione
Ad esempio per classificare il sillogismo
Tutti i gufi sono rapaci (premessa maggiore)
Nessun rapace è una erbivoro (premessa minore)
Nessuna erbivoro è un gufo (conclusione)
Il modo è AEE mentre la figura è la IV poiché nella premessa maggiore
troviamo prima il predicato e poi il termine medio (PM) , mentre nella
premessa minore si ha prima il termine medio e poi il soggetto (MS) .

19. Regole
In epoca medioevale la logica aristotelica fu perfezionata. Si introdusse la IV
figura e 8 regole fondamentali per riconoscere i sillogismi validi da quelli
errati; se anche una sola di queste regole non è rispettata, il sillogismo,
inevitabilmente, sarà scorretto.
Infine, i medievali introdussero una curiosa filastrocca che permette di
individuare i sillogismo corretti, validi.

20. 8 regole
1. Ci devono essere solo tre termini (soggetto, predicato e termine medio).
2. Il soggetto e il predicato devono essere distribuiti in modo uguale nelle
premesse e nella conclusione.
3. Il termine medio non deve mai comparire nella conclusione.
4. Il termine medio deve essere distribuito in almeno una delle due
premesse.
5. Da due premesse negative non segue alcuna conclusione.
6. Da due premesse affermative segue una conclusione affermativa.
7. Da due premesse particolari non segue alcuna conclusione.
8. Se una delle due premesse è negativa, la conclusione dovrà essere
negativa; se una delle due premesse è particolare, la conclusione dovrà
essere particolare.

21. La filastrocca
Grazie a queste regole solo 19 sono i sillogismi risolubili, ovvero validi! In
particolare i logici medioevali inventarono un espediente per ricordare i
19 modi dei sillogismi corretti. L’espediente trovato fu quello di dare un
nome, ovviamente in latino, ad ogni modo valido del sillogismo, affinché,
attraverso di esso, si potesse identificare quali fossero i tre enunciati
componenti. I nomi dovevano quindi contenere le vocali dei modi
validi per ognuna delle 4 figure.
Costruirono così la seguente “filastrocca latina”.

22. Filastrocca latina
I figura MP-SM BARBARA CELARENT DARII
FERIO
II figura PM-SM CESARE CAMESTRES
FESTINO BAROCO
III figura MP
MS
DARAPTI DISAMIS DATISI
FELAPTON BOCARDO
FERISON
IV figura PM
MS
BRAMANTIP CAMENES
DIMARIS FESAPO FRESISON

23. Come si usa la filastrocca per
risolvere un sillogismo ?
PM: Nessun uomo è un vivente con quattro zampe E
Pm: Alcuni viventi con quattro zampe sono animali I
C : ?
Forma: PM – MS --> IV figura. Modo: EI
In tabella, alla IV fig, la parola che contiene E ed I come prime due vocali è
fresison. Quindi la conclusione deve essere un enunciato di tipo O,
ovvero particolare negativo, il cui soggetto è “animali” e il cui predicato
è “uomini”. La conclusione pertanto è:
C: Alcuni animali non sono uomini.

24. Quanti sono i possibili
sillogismi
Ogni sillogismo e' composto di 3 giudizi (M-S-P) ed i giudizi sono di 4 tipi
(forme) diversi (A, E, I, O), per 4 figure possibili (I, II, III, IV)
Quindi posso fare tanti sillogismi quante sono le disposizioni con ripetizione
di 4 oggetti presi 3 a 3,
D'4;3 = 4ⁿ = 64, il tutto moltiplicato per 4 figure possibili
→ 64. 4 = 256
Dunque ci sono 256 possibili tipi diversi di sillogismo di cui soltanto i 19 che
abbiamo visto sono corretti.

25. Verità e validità di un sillogismo
Un sillogismo è considerato valido se rispetta le regole di derivazione, cioè
se è formalmente corretto. La validità di un sillogismo non dipende dalla
verità delle affermazioni che lo compongono. Sicché il sillogismo:
Ogni animale vola
L 'asino è un animale
Dunque l'asino vola
è valido, anche se le proposizioni che lo compongono non sono vere, e la
conclusione scaturisce correttamente da una Premessa Maggiore
palesemente falsa.

26. Ragion sufficiente
Attenzione: Condizione necessaria e sufficiente della validità di un
sillogismo è il rispetto delle regole formali, non la verità delle singole
proposizioni, la quale, da sola, non è condizione sufficiente. Ad es.
Gli dei sono immortali
Gli uomini non sono dei
Dunque gli uomini non sono immortali.
Ogni affermazione, in sé considerata, è vera, ma viene derivata in modo
sbagliato: la PM infatti dice che tutti gli dei sono immortali, ma non che
tutti gli immortali sono dei. Data la premessa, io non posso escludere che
ci sia qualche immortale che non sia un dio, tra cui l'uomo.
Questo sillogismo è vero, ma non è valido. Si provi a verificarlo con Eulero-
Venn

27. Trasformazioni nella logica dei
predicati
Un sillogismo è dunque fatto da tre proposizioni: S, M e P
Tutti gli uomini sono mortali è fatta da “x è un uomo” (M) ed “x è mortale”
(P)
Socrate è un uomo è fatta da “x è Socrate” (S) e da M ( “x è un uomo”),
Socrate è mortale è fatta da “x è Socrate” (S) ed “x è mortale” (P)
Quindi: MP -SM – SP
Sillogismo di I figura (vedi Tav. 2)

28. Trasformazioni nella logica dei
predicati (Modus Barbara, Figura I)
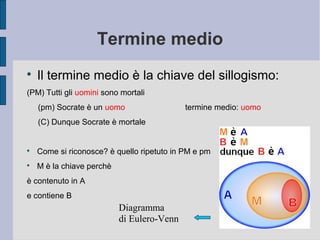
Tutti gli uomini (M) sono mortali (P)
I greci (S) sono uomini (M)
I greci (S) sono mortali (P) (Modus Barbara, Figura I)
∀x [(Mx → Px) Ʌ (Sx → Mx)] → (Sx → Px) (forma 1)
Si legge:
per ogni x, [(se x è M allora x è P) and (se x è S allora x è M)]
allora (se x è S allora x è P)

29. Trasformazioni nella logica dei
predicati
Ricordando che M → P = ¬ (M Ʌ ¬P) si ha che
(forma 2)

30. Trasformazioni nella logica dei
predicati
Sia la forma 1 che la 2 sono equivalenti, e
verificabili mediante il calcolo verofunzionale
col consueto metodo delle tavole di verità,
per cui il valore di verità dell'intera forma
proposizionale deve essere, se il sillogismo è
valido, sempre VERO.
→ Esercizi. Pagina di wikipedia sul sillogismo.

31. Come verificare la validità di un
sillogismo categorico?
Riassumendo, ci sono 3 metodi
1) Ragionare sul diagramma di Eulero-Venn
2) Applicare il metodo della filastrocca latina
3) Trasformare, con la logica dei predicati, il
sillogismo nelle proposizioni atomiche che lo
compongono, e poi verificarlo con il calcolo
verofunzionale.

32. Il sillogismo ipotetico
1. Se Pippi è un gatto allora ha la coda (PM)
Pippi è un gatto (pm) → Quindi Pippi ha la coda ( C )
2. Se Pippi è un gatto allora ha la coda (PM)
Pippi non è un gatto (pm) → Quindi Pippi non ha la coda ( C )
3. Se Pippi è un gatto allora ha la coda (PM)
Pippi ha la coda (pm) → Quindi Pippi è un gatto ( C )
4. Se Pippi è un gatto allora ha la coda (PM)
Pippi non ha la coda (pm) → Quindi Pippi non è un gatto ( C )

33. Il sillogismo ipotetico
Quali sono validi? Il 1° ed il 4°
Si basano sul modus ponens e modus tollens, due forme di ragionamento
deduttivo definite da Crisippo, logico stoico del III sec. a.C.
Modus ponendo ponens e
Modus tollendo tollens
Il 2° ed il 3° sono due fallacie dette negazione dell’antecedente (il 2°) e
affermazione del conseguente (3°)

34. Modus ponens e modus tollens
Modus ponens.
Se Pippi è un gatto allora ha la coda (PM)
Pippi è un gatto (pm) → Quindi Pippi ha la coda ( C )
[(p → q) p] → qɅ
Modus tollens
Se Pippi è un gatto allora ha la coda (PM)
Pippi non ha la coda (pm) → Quindi Pippi non è un gatto ( C )
[(p → q) Ʌ ¬q] → ¬p

35. Fallacie
Negazione dell'antecedente
2. Se Pippi è un gatto (p) allora ha la coda (q)
Pippi non è un gatto (¬p) → Quindi Pippi non ha la coda ( ¬q )
Affermazione del conseguente
3. Se Pippi è un gatto (p) allora ha la coda (q)
Pippi ha la coda (q) → Quindi Pippi è un gatto ( p )
[(p → q) q] → pɅ

36. Schema risolutivo per il
sillogismo ipotetico
Modus ponendo
ponens
Modus tollendo
tollens
Negazione
dell’antecedente
Affermazione
Delconseguent
e
(p → q) Ʌ
p
_____________
→ q
(p → q) Ʌ
¬ q______________
→ ¬ p
(p → q) Ʌ
¬ p_______________
→ ¬ q
(p → q) Ʌ
q____________
→ p

37. Sillogismo disgiuntivo
ll sillogismo disgiuntivo (detto anche modus tollendo ponens) è una regola
d'inferenza che ha come PM una disgiunzione (inclusiva od
esclusiva)dunque, se un termine è falso, l'altro è sicuramente vero.
[(p V q) Ʌ ¬q] → p
Oggi vado al cinema o vado in piscina.(p V q)
Ma non vado in piscina.(¬q)
Dunque, oggi vado al cinema.(p )
Se si danno due ipotesi disgiunte P o Q, e si nega una delle due ipotesi,
per la regola della disgiunzione si potrà inferire Q. La disgiunzione è
falsa solo se entrambi gli enunciati sono falsi. Essendo la disgiunzione
data per vera come premessa almeno uno dei due termini dev'essere
vero.

38. Simboli
∃ ∀ Ʌ ¬ ∈