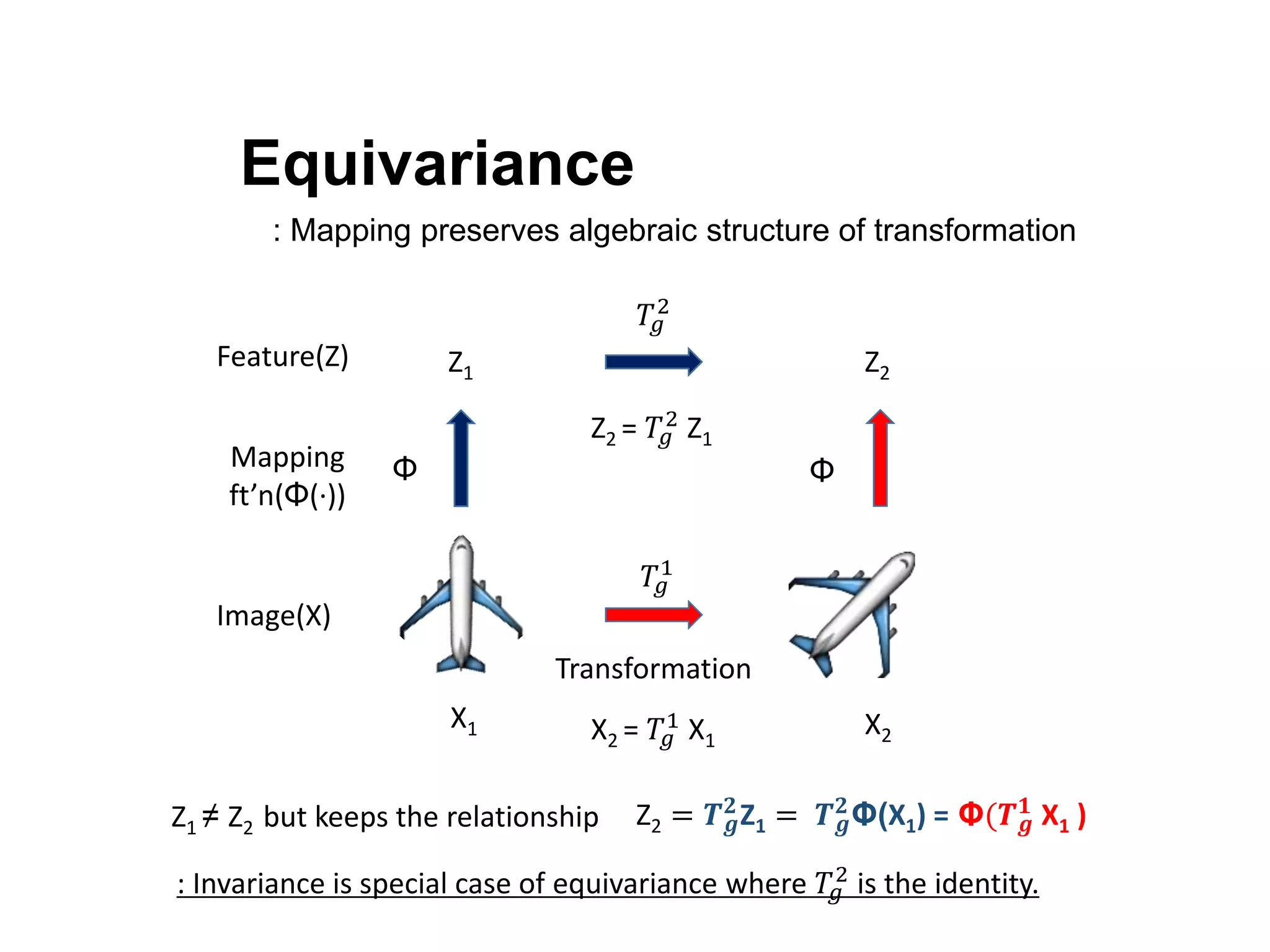
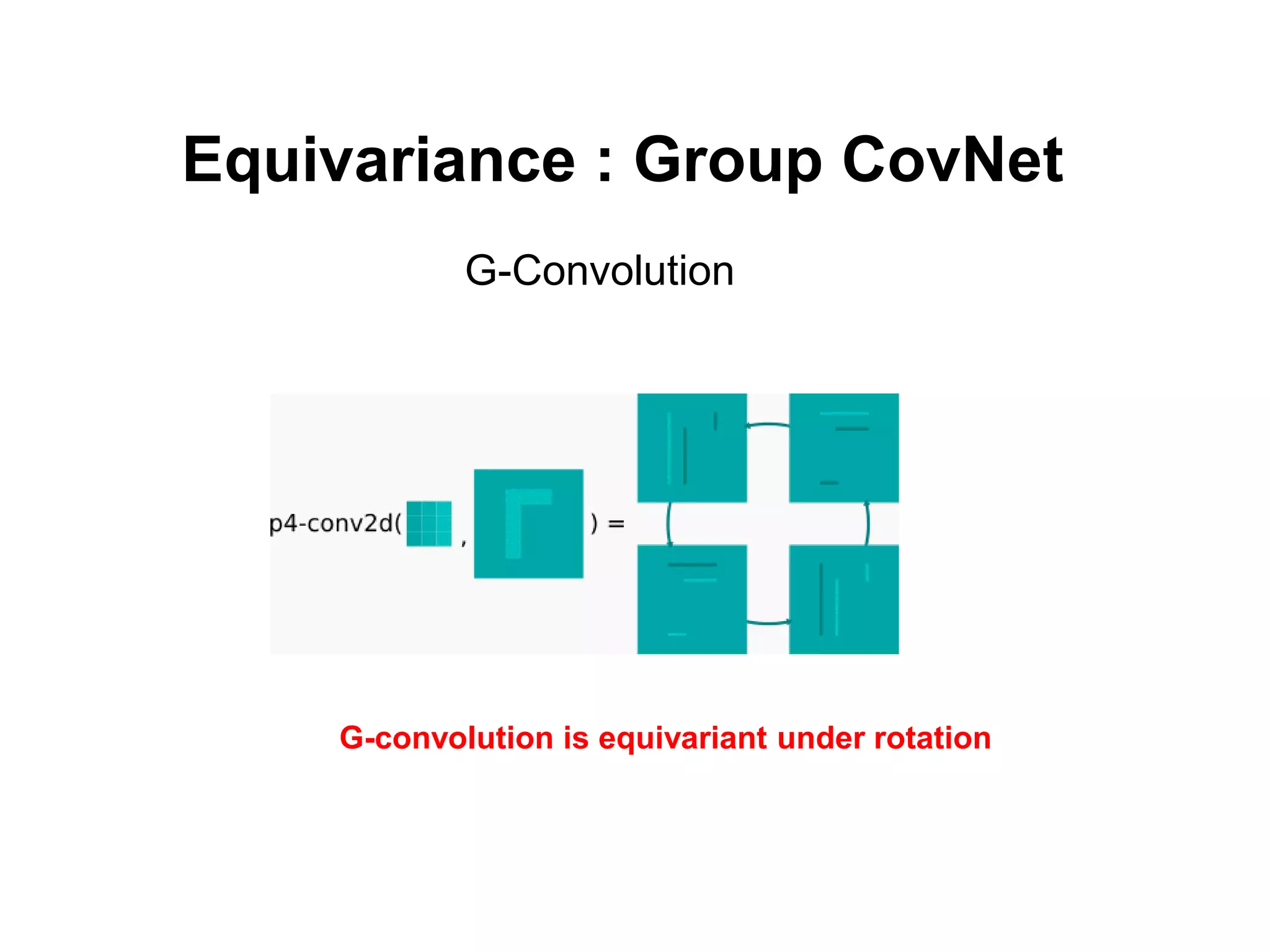
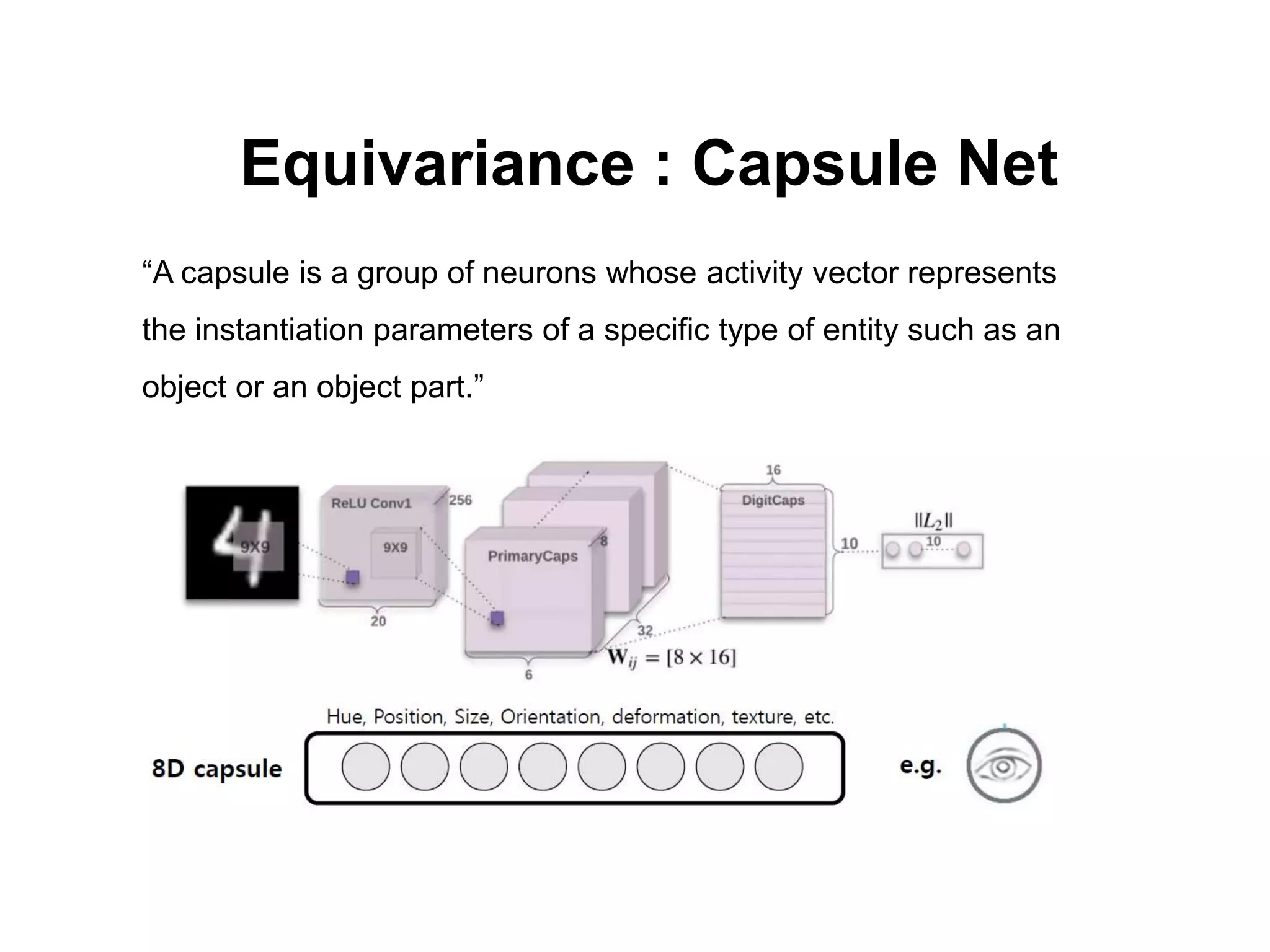
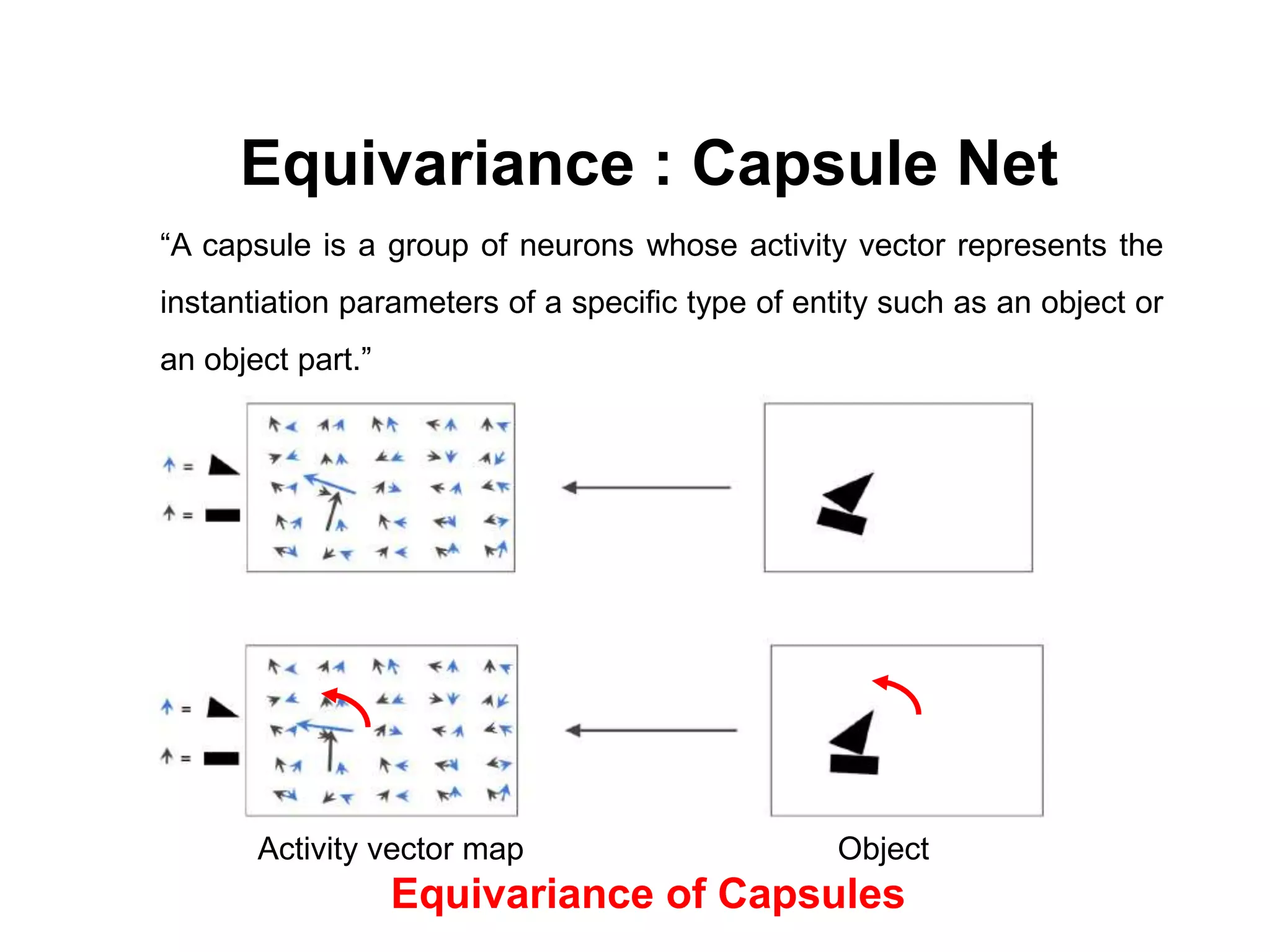
The document discusses the limitations of conventional convolutional neural networks (CNNs), particularly their equivariance under translation but not under rotation. It introduces group convolutional networks (g-CNNs) that utilize a group of filters to achieve equivariance, allowing for better recognition of features across different orientations. Additionally, it explores the concept of capsules in neural networks, which represent instantiation parameters for objects and contribute to understanding equivariance.

1. Brief intro : Invariance and Equivariance

2. CovNet are translational Equivalent
This demonstrates LeNet-5's invariance to small rotations (+/-40 degrees).
How about Rotation ?
Limitation of Conventional CovNet

3. 2D convolution is equivariant under translation, but not under rotation
Limitation of Conventional CovNet

4. Invariance
Φ
Image(X)
Feature(Z) Z1 = Z = Z2
𝑇𝑔
1
Mapping
ft’n(Φ(·))
Φ
Transformation
X1 X2
Z = Z1 = Φ(X1) = Z2 = Φ(X2) = Φ(𝑻 𝒈
𝟏
X1 )
: Mapping independent of transformation, 𝑇𝑔, for all 𝑇𝑔
X2 = 𝑇𝑔
1
X1

5. To make a Convolutional Neural Networks (CNN) transformation-
invariant, data augmentation with training samples is generally used
Invariance

6. Equivariance
Φ
Image(X)
Feature(Z) Z1 Z2
𝑇𝑔
2
𝑇𝑔
1
Φ
Transformation
X1 X2
Z2 = 𝑻 𝒈
𝟐
Z1 = 𝑻 𝒈
𝟐
Φ(X1) = Φ(𝑻 𝒈
𝟏
X1 )
: Invariance is special case of equivariance where 𝑇𝑔
2 is the identity.
X2 = 𝑇𝑔
1
X1
Z2 = 𝑇𝑔
2
Z1
: Mapping preserves algebraic structure of transformation
Z1 ≠ Z2 but keeps the relationship
Mapping
ft’n(Φ(·))

7. Equivariance : Group CovNet
To understand the rotation or proportion change of a given entity, a
group of filters(a combination of rotated and mirror reflected versions of
filter) is adopted.
For example, the group p4 which contains translations and rotations by
multiples of ninety degrees, or, which additionally contains mirror
reflections.
: Rotation
: Mirror reflections

8. A filter in a G-CNN detects co-occurrences of features that have the
preferred relative pose, and can match such a feature constellation in
every global pose through an operation called the G-convolution.
Equivariance : Group CovNet
Filter group 1
Filter group 2
Filter group N

9. Visualization of classic 2D convolution
Visualization of the G-Conv for the roto-translation group
G-Convolution
Equivariance : Group CovNet

10. G-convolution is equivariant under rotation
G-Convolution
Equivariance : Group CovNet

11. Equivariance : Group CovNet
Latent representations learnt by a CNN and a G-CNN.
- The left part is the result of a typical CNN while the right one is that of a G-
CNN.
- In both parts, the outer cycles consist of the rotated images while the inner
cycles consist of the learnt representations.
- Features produced by a G-CNN is equivariant to rotation while that produced
by a typical CNN is not.

12. What we need : EQUIVARIANCE (not invariance)
“Equivariance makes a CNN understand the rotation or proportion change”
Equivariance : Capsule Net

13. “A capsule is a group of neurons whose activity vector represents
the instantiation parameters of a specific type of entity such as an
object or an object part.”
Equivariance : Capsule Net

14. Equivariance of Capsules
“A capsule is a group of neurons whose activity vector represents the
instantiation parameters of a specific type of entity such as an object or
an object part.”
Activity vector map Object
Equivariance : Capsule Net