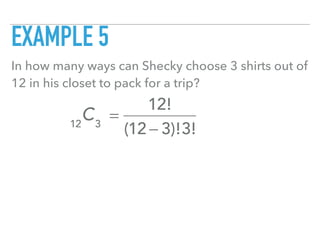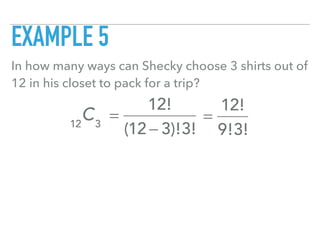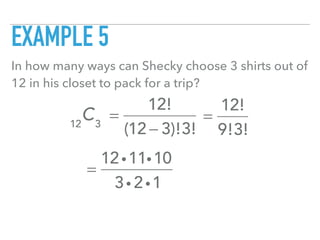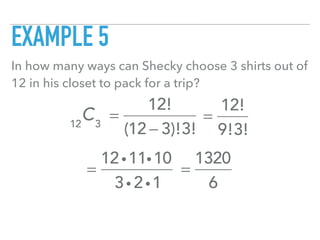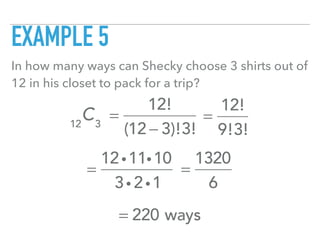This document discusses permutations and combinations. Permutations refer to arrangements where order matters, while combinations refer to arrangements where order does not matter. Formulas for calculating permutations and combinations are provided. Several examples are worked through to demonstrate calculating permutations and combinations for different scenarios such as choosing passwords, selecting movies, and arranging binders on a shelf.

1. PERMUTATIONS AND
COMBINATIONS
SECTION 0-5

2. ESSENTIAL QUESTION
‣ How do you solve problems involving
permutations and combinations?

3. VOCABULARY
1. Permutation:
2. Linear Permutation:
3. Combination:

4. VOCABULARY
1. Permutation:
2. Linear Permutation:
3. Combination:
The number of ways in which a set
of things can be arranged when order
matters

5. VOCABULARY
1. Permutation:
2. Linear Permutation:
3. Combination:
The number of ways in which a set
of things can be arranged when order
matters
The arrangement of objects
in a line

6. VOCABULARY
1. Permutation:
2. Linear Permutation:
3. Combination:
The number of ways in which a set
of things can be arranged when order
matters
The arrangement of objects
in a line
The number of ways in which a set
of things can be arranged when order does
not matter

7. FORMULAS
1. Permutation:
2. Permutation with Repetition (n objects of which p
and q, etc. are alike:
3. Combination:

8. FORMULAS
1. Permutation:
2. Permutation with Repetition (n objects of which p
and q, etc. are alike:
3. Combination:
n
Pr
=
n!
(n − r)!

9. FORMULAS
1. Permutation:
2. Permutation with Repetition (n objects of which p
and q, etc. are alike:
3. Combination:
n
Pr
=
n!
(n − r)!
n!
p!q!

10. FORMULAS
1. Permutation:
2. Permutation with Repetition (n objects of which p
and q, etc. are alike:
3. Combination:
n
Pr
=
n!
(n − r)!
n!
p!q!
n
Cr
=
n!
(n − r)!r!

11. EXAMPLE 1
Determine whether each situation involves a
permutation or a combination.
a. Choosing a 4-digit password
b. Selecting 3 movies out of 20 possibilities on Netflix
c. Choosing 5 students out of a class of 28 to plan a class party
d. Scheduling 6 students to each work an hour selling raffle
tickets

12. EXAMPLE 1
Determine whether each situation involves a
permutation or a combination.
a. Choosing a 4-digit password
b. Selecting 3 movies out of 20 possibilities on Netflix
c. Choosing 5 students out of a class of 28 to plan a class party
d. Scheduling 6 students to each work an hour selling raffle
tickets
Permutation

13. EXAMPLE 1
Determine whether each situation involves a
permutation or a combination.
a. Choosing a 4-digit password
b. Selecting 3 movies out of 20 possibilities on Netflix
c. Choosing 5 students out of a class of 28 to plan a class party
d. Scheduling 6 students to each work an hour selling raffle
tickets
Permutation
Combination

14. EXAMPLE 1
Determine whether each situation involves a
permutation or a combination.
a. Choosing a 4-digit password
b. Selecting 3 movies out of 20 possibilities on Netflix
c. Choosing 5 students out of a class of 28 to plan a class party
d. Scheduling 6 students to each work an hour selling raffle
tickets
Permutation
Combination
Combination

15. EXAMPLE 1
Determine whether each situation involves a
permutation or a combination.
a. Choosing a 4-digit password
b. Selecting 3 movies out of 20 possibilities on Netflix
c. Choosing 5 students out of a class of 28 to plan a class party
d. Scheduling 6 students to each work an hour selling raffle
tickets
Permutation
Combination
Combination
Permutation

16. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4

17. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!

18. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!
=
7!
3!

19. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!
=
7!
3!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1

20. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!
=
7!
3!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1

21. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!
=
7!
3!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1

22. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!
=
7!
3!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1

23. EXAMPLE 2
Calculate the following permutations and
combinations.
a. 7
P4
=
7!
(7− 4)!
=
7!
3!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1
= 840 ways

24. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4

25. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!

26. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!

27. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1i 3i 2i1

28. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1i 3i 2i1

29. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1i 3i 2i1

30. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1i 3i 2i1

31. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1i 3i 2i1

32. EXAMPLE 2
Calculate the following permutations and
combinations.
b. 7
C4
=
7!
(7− 4)!4!
=
7!
3!4!
=
7i 6 i 5i 4 i 3i 2i1
3i 2i1i 3i 2i1
= 140 ways

33. EXAMPLE 3
Fuzzy Jeff has a 4-digit passcode for his iPad. The
code is made up of the odd digits: 1, 3, 5, 7, and 9.
If each digit can be used only once, how many
different codes are available?

34. EXAMPLE 3
Fuzzy Jeff has a 4-digit passcode for his iPad. The
code is made up of the odd digits: 1, 3, 5, 7, and 9.
If each digit can be used only once, how many
different codes are available?
5
P4

35. EXAMPLE 3
Fuzzy Jeff has a 4-digit passcode for his iPad. The
code is made up of the odd digits: 1, 3, 5, 7, and 9.
If each digit can be used only once, how many
different codes are available?
5
P4
=
5!
(5 − 4)!

36. EXAMPLE 3
Fuzzy Jeff has a 4-digit passcode for his iPad. The
code is made up of the odd digits: 1, 3, 5, 7, and 9.
If each digit can be used only once, how many
different codes are available?
5
P4
=
5!
(5 − 4)!
=
5!
1!

37. EXAMPLE 3
Fuzzy Jeff has a 4-digit passcode for his iPad. The
code is made up of the odd digits: 1, 3, 5, 7, and 9.
If each digit can be used only once, how many
different codes are available?
5
P4
=
5!
(5 − 4)!
=
5!
1!
= 5i 4 i 3i 2

38. EXAMPLE 3
Fuzzy Jeff has a 4-digit passcode for his iPad. The
code is made up of the odd digits: 1, 3, 5, 7, and 9.
If each digit can be used only once, how many
different codes are available?
5
P4
=
5!
(5 − 4)!
=
5!
1!
= 5i 4 i 3i 2
= 120 codes

39. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?

40. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!

41. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!
=
16 i15i14 i13i12i11i10 i 9 i 8
5i 4 i 3i 2i1i 4 i 3i 2i1

42. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!
=
16 i15i14 i13i12i11i10 i 9 i 8
5i 4 i 3i 2i1i 4 i 3i 2i1

43. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!
=
16 i15i14 i13i12i11i10 i 9 i 8
5i 4 i 3i 2i1i 4 i 3i 2i1

44. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!
=
16 i15i14 i13i12i11i10 i 9 i 8
5i 4 i 3i 2i1i 4 i 3i 2i1

45. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!
=
16 i15i14 i13i12i11i10 i 9 i 8
5i 4 i 3i 2i1i 4 i 3i 2i1
= 14 i13i11i10 i 9 i 8

46. EXAMPLE 4
In how many ways can 7 white binders, 5 red
binders, and 4 blue binders be arranged on a shelf?
16!
7!5!4!
=
16 i15i14 i13i12i11i10 i 9 i 8
5i 4 i 3i 2i1i 4 i 3i 2i1
= 14 i13i11i10 i 9 i 8
= 1,441,440 ways

47. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?

48. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?
12
C3

49. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?
12
C3
=
12!
(12 − 3)!3!

50. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?
12
C3
=
12!
(12 − 3)!3!
=
12!
9!3!

51. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?
12
C3
=
12!
(12 − 3)!3!
=
12!
9!3!
=
12i11i10
3i 2i1

52. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?
12
C3
=
12!
(12 − 3)!3!
=
12!
9!3!
=
12i11i10
3i 2i1
=
1320
6

53. EXAMPLE 5
In how many ways can Shecky choose 3 shirts out of
12 in his closet to pack for a trip?
12
C3
=
12!
(12 − 3)!3!
=
12!
9!3!
=
12i11i10
3i 2i1
= 220 ways
=
1320
6

54. SUMMARY
Describe the difference between permutations and
combinations.