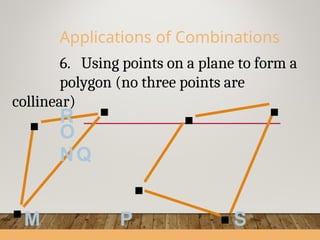
The document covers the concepts of permutations and combinations, explaining how to find possible arrangements and selections of objects. It provides examples showcasing applications such as ranking locations, arranging news stories, and selecting questions from tests. The document emphasizes the importance of understanding factorials and the rules for calculating permutations and combinations.

1. WARM UP – FINDTHE
MEAN ANDTHE
STANDARD DEVIATION.

2. WARM UP – FINDTHE MEAN
AND STANDARD DEVIATION

3. PERMUTATIONS AND
COMBINATION
SOLVES PROBLEMS ON

4. OBJECTIVE
•Find Sample Space
using Permutations
and Combinations

5. RELEVANCE
•Learn various methods of
finding out how many possible
outcomes of a probability
experiment are possible.
•Use this information to find
probability.

6. DEFINITION……
• Permutation – an arrangement of objects in a specific order.
Order Matters!

7. EXAMPLE……
• How many ways can you arrange 3
people for a picture?
• Note: You are using all 3 people
• Answer:
6
1
2
3 



8. FACTORIAL……
• This is the same as using a
factorial:
• Using the previous example:
1
).....
2
)(
1
(
! 

 n
n
n
n
)
2
3
)(
1
3
(
3
!
3 


6
1
2
3
!
3 




9. EXAMPLE……
• Suppose a business owner
has a choice of 5 locations
in which to establish her
business. She decides to
rank them from best to
least according to certain
criteria. How many
different ways can she
rank them?
• Answer:
• Note: She ranked ALL 5
locations.
120
1
2
3
4
5
!
5 






10. • What if she only
wanted to rank the
top 3?
• Answer:
• This is no longer a
factorial problem because
you don’t rank ALL of
them.
60
3
4
5 



11. PERMUTATION RULE……
where n = total # of
objects and r = how
many you need.
“n objects taken r at a
time”
)!
(
!
r
n
n
Pr
n



12. • Remember the business
woman who only
wanted to rank the top
3 out of 5 places?
• This is a
permutation:
60
3
4
5 


60
2
120
!
2
!
5
)!
3
5
(
!
5
3
5 




P

13. EXAMPLE……
• ATV news director wishes to
use 3 news stories on the
evening news. She wants the
top 3 news stories out of 8
possible. How many ways can
the program be set up?
• Answer:
336
3
8 
P

14. EXAMPLE……
• How many ways can a
chairperson and an assistant
be selected for a project if
there are 7 scientists
available?
• Answer:
42
2
7 
P

15. EXAMPLE……
• How many different
ways can I arrange 3
box cars selected
from 8 to make a
train?
• Answer:
336
3
8 
P

16. EXAMPLE……
• How many ways can 4
books be arranged on
a shelf if they can be
selected from 9 books?
• Answer:
3024
4
9 
P

17. A FACTORIAL IS ALSO A
PERMUTATION……
• How many ways
can 4 books be
arranged on a
shelf?
• You can do 4! or you
can set it up as a
permutation.
Answer:
24
4
4 
P

18. EXAMPLE……
• Find the permutations of the word
Mississippi.
• Number of Letters
• 11 –Total Letters
• 1 – M
• 4 – I
• 4 – S
• 2 - P
• Answer:
• You can eliminate the 1!’s because
they are equal to 1.
34650
)
!
2
!
4
!
4
!
1
(
!
11


19. NOTE……
•0! = 1
and
1! = 1

20. •How many
permutations of the
word seem can be
made?
• Answer:
12
!
2
!
4


21. THIS LEADS TO ANOTHER
PERMUTATION RULE WHEN
SOME THINGS REPEAT……
• It reads: the # of permutations of n
objects in which k1 are alike, k2 are alike,
etc.
!
!...
!
!
!
3
2
1 p
r
n
k
k
k
k
n
P 

22. IT’SYOUR TURN
• Example: How many permutations of the word
volleyball can be made?

23. COMBINATIO
N
1. In an essay test, there 5 questions given
where you can choose only 3 of them to
answer. How many ways can you select
questions to answer?
5C3 =5!
5-3 ! 3!
5!
5C3 =
2! 3!
5c3 = 10
There are 10 ways.

24. 2.
COMBINATION
In a limited party, there are 8
persons present. If each of them shake
hands exactly with one another, how
many handshakes are there?
8!
=
8 − 2 ! 2!
8!
=
6! 2!
There are 28 handshakes.
= 28

25. COMBINATIO
N
2. How many groups composed of 4 persons
each can be formed from 7 students?
= n!
n-r !r!
7!
5C4
7 − 4 ! 4!
7!
3! 4!
7C4 =35
There are 35 groups.

26. Other Problems Involving
Combinations
4. From 7 Math books and 6 Science
books, in how many ways can you
select 8 books if the number of Math
books to be bought is equal to the
number of Science books?
7 4 ∙ 6 4
35 ∙ 15
525 ways

27. Example 2:
In a meeting, it is required to seat 4 women and 5 men
in a row so that the women occupy the even places. How
many arrangements are possible?
Solution:
The total number of places is 9.
The even places are 2nd, 4th, 6th, 8th.
The 4 women can be arranged occupying even places in
P (4, 4) = 24 ways.
Five men can be arranged on the remaining 5 places in
P (5, 5) = 120 ways.
The numbers of arrangements are,
P (4, 4) • P(5,5)
24 • 120 = 2,880 ways

29. Applications of Combinations
6. Using points on a plane to form a
polygon (no three points are
collinear)
R
O
NQ
M P S
. .
.
.
. .
.